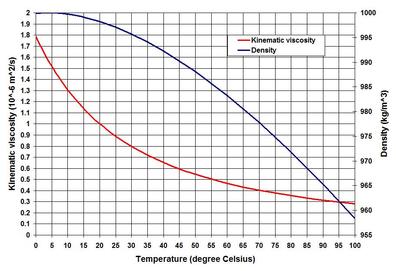
 The title of this piece has a very broad range of subtopics – some of which have already been discussed previously on this website. In this piece let us talk about some properties of coastal water – the properties that appear in most methods and equations of coastal hydraulic science and engineering – as referred to in some pieces on the NATURE and SCIENCE & TECHNOLOGY pages. In brief, these properties include the mass of coastal water, its resistance to sliding motion, and its resistance to compression. These three properties – the seawater equation of state, viscosity and compressibility are most interesting to physicists and engineers. When one thinks of coastal water – some common views immediately appear – close to the sources of freshwater such as river mouths and estuaries it is brackish (diluted mix of fresh and salt water) – further away from the source it is close to seawater salinity. It is mostly mixed in the top surface layer and in waters where the basin aspect ratio (ratio of vertical and horizontal dimensions) is very low, but is stratified to some degree in basins of high aspect ratio. The stratification – in terms of both temperature and salinity – in sharp lines of distinctions is known as thermocline and halocline, respectively. I have touched upon the stability of stratification in the Turbulence piece – but there are more on the topic – hope to come back to that at some other time. . . . Before going further I am tempted to make one important observation. This is the fact that the variability of these parameters in coastal waters is so negligible that coastal engineering literature has very little room discussing them. In the Delft lectures of coastal engineering, we were told that one of the key words for practicing engineers was approximation – approximation! In the coastal and estuarine oceanographic lectures at the USC, professors did not forget to mention that mistakes in the use of different but close numbers in density and viscosity were very negligible. Although approximation is one of the major techniques in every branch of social and Natural sciences, it has a particular significance to the practicing engineers because they often find comfort in hanging on to a certain number – reasonable enough to justify and safe enough for their problems. Despite such a view, unless one understands the science of seawater physical properties, it is often impossible for him or her to overcome the feeling of uncertainty. This certainly applies to the blue-water oceanographic investigators who cannot afford to ignore the variability of seawater properties, because they deal with depth scales in the order of 100s of meters and length scales in the order of kilometers. . . . The 2010 UNESCO document on seawater thermodynamics is one of the most extensive recent treatises on the seawater equation of state. It expresses seawater density as a function of salinity, temperature and pressure. The density (mass per unit volume) is also often expressed as specific volume (reciprocal of density) and specific gravity (the ratio of density of any matter and the density of freshwater at standard temperature of 4 degree Celsius) – is not the unit of force like the specific weight (density times the acceleration due to gravity). In oceanographic literature, the seawater density is usually shown as an anomaly – as sigma-t. This anomaly is just a way of expressing things for convenience, and is nothing but the density of seawater in excess of the freshwater density of 1000 kilogram per cubic meter of volume (kg/m^3). Most old oceanographic literature used to present the complicated equation of state as a graphical method until the UNESCO elaboration was published. For all practical purposes, the polynomial UNESCO method is approximated as a linear equation that comes with an error of ± 0.5 kg/m^3. Among the three independent variables, pressure has the least influence on seawater density – which in essence tells that water is very negligibly compressible. The fluid pressures are usually measured in bars (1 bar equals to a pressure of 100 kiloPascal or kPa) – the atmospheric pressure on the Earth’s surface is 1000 millibar or 1 bar; and 1 meter of water exerts a pressure of 1 decibar (=10 kPa; this is the usual unit used for water pressure). Other influences remaining constant, the water density increases by only 1 kg/m^3 in every 200 meter (or 200 decibar) of depth increase. The water density has a strange relationship to temperature – the freshwater density is the highest 1000 kg/m^3 at a temperature of 4 degree Celsius – but decreases in both higher and lower temperatures from this threshold value (note that the mean ocean temperature is about 3.5 degree Celsius). As a rule of thumb, water density decreases by 1 kg/m^3 for every 5 degree Celsius rise of water temperature. But as shown in the image, the relationship between water density and temperature is far from linear – so is viscosity. I will come back to viscosity later, before that let me elaborate some other aspects of seawater salinity. Among the three parameters, salinity affects the seawater density more than any other. It was used to be measured as a gram of salt in one kilogram of solution, and presented in units of parts per thousand (ppt or o/oo). Salinity is now referred to as Sp on the unit-less Practical Salinity Scale or PSS-78 following the 1978 UNESCO definition. The PSS is defined as the ratio of seawater conductivity to the conductivity of standard KCL solution. For all practical purposes the two systems – ppt and Sp are equivalent, but Sp applies in the range from 2 to 42. The average seawater salinity is about 35 Sp – the highest ocean water salinity is concentrated in the sub-tropical gyre region between 20 and 30 degree North and South latitudes where rainfall is the lowest. Some orders of magnitude seawater density for salinity? For 5, 10, 20, 30 and 35 Sp, the corresponding densities are 1003.6, 1007.5, 1015.3, 1023.1 and 1027.0 kg/m^3 in 1-meter depth of water at a temperature of 10 degree Celsius. For most coastal engineering problems, a density of 1025 kg/m^3 is applied. If one uses 1000 kg/m^3 instead of 1025 kg/m^3, the incurred error is only 2.5%. . . . Let us now turn our attention to viscosity (a term reciprocal to fluidity). This water characteristic – the molecular viscosity (as opposed to the eddy viscosity discussed in the Turbulence piece) is a dynamic property – it is the resistance of water to shearing or sliding motion. It was formulated by none other than Newton (Isaac Newton, 1643 – 1727) as a proportionality coefficient in the relation between shear stress and shearing rate of deformation. The fluids such as water that have a constant proportionality coefficient are known as the Newtonian fluids. The coefficient is known as the dynamic viscosity coefficient – a product of density and kinematic viscosity. While viscosity is a function of density, in many applications it appears as the kinematic viscosity – as a matter of convenience in managing equation terms in the cases of homogenous water of equal density. In some other cases of fluid mechanics problems, the effect of viscosity is so low that the term is neglected all-together, giving rise to the term inviscid fluid or ideal fluid. The included image shows the kinematic viscosity as a function of temperature. The kinematic viscosity of freshwater at 20 degree Celsius is about 1*10^-6 meter squared per second – the air viscosity is about 1/50th of water. Let us now turn our attention to the last term – the compressibility. This term refers to resistance to change in volume in response to change in pressure. It is reciprocal to the volume or bulk modulus of elasticity (BME) – a coefficient defining the change in pressure in response to change in volume. The definition of BME originates from the Hooke’s (English mathematician Robert Hooke, 1635 – 1703) Law of stress and strain; and Young’s (English scientist Thomas Young, 1773 – 1829) modulus of elasticity. The water BME increases with high pressure but has a strange relationship with temperature – it is highest at 50 degree Celsius – decreasing in both higher and lower temperatures. The higher the value of the BME, the lower is the compressibility. The typical water BME is 2.2 million kPa. Such a high BME means that water needs very high pressure to change in volume – or to be compressible – leading to the common assumption that water is incompressible. One of the implications of very low compressibility of water is that the speed of sound is very high in water – some 1500 meter per second – about 4 to 5 times faster than the speed in air. The speed of sound increases as water temperature, salinity and depth are increased. . . . Well there is much more on water properties than what are discussed. For now, let us leave it at this – on this wonder substance called water – a breeder and sustainer of life. Let us finish this piece with a word of wisdom from Lao Tzu: nothing is softer or more flexible than water, yet nothing can resist it. . . . . . - by Dr. Dilip K. Barua, 1 December 2016
1 Comment
|

 RSS Feed
RSS Feed
