Turbulence

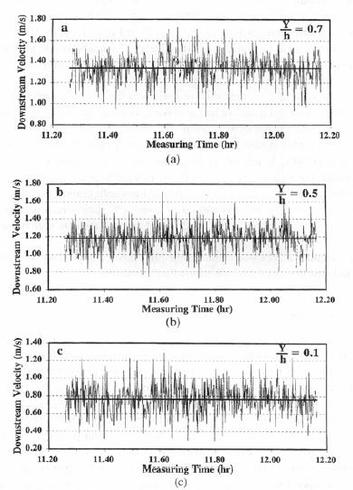
In this piece let us talk about another important phenomenon in the field of fluid mechanics – turbulence – focusing primarily on its processes and characteristics. To do this I will take help from my 1998 Journal of Hydraulic Research paper: Some aspects of turbulent flow structure in large alluvial rivers. This paper was presented in the 1995 International Conference on Coherent Flow Structures in Open Channels at the University of Leeds. I have included an image from this paper (courtesy Taylor & Francis) to illustrate the nature of turbulence in time at different depths of the water column (Y is height above bed and h is water depth). It was based on field measurements of river currents in the Brahmaputra-Jamuna River in Bangladesh by Acoustic Doppler Current Profiler (ADCP). Conducted under the auspices of Delft-DHI Consortium, European Union and Bangladesh Government – the data reduction of measurements was performed by HYMOS database software of Delft Hydraulics.
.  .  .
What is turbulence? It is the three-dimensional random eddy motions or vortices of various time-scales and sizes in fluid flows. It is a very irregular and erratic fluid motion discernible in both space and time. In space it is visible as a rotational eddy – large and small, and in time as a spike – high and low. Some of the turbulent motions are very small – born quickly, only to die quickly as well. The large ones linger longer to be transported and transformed by the mean flow. The terms turbulence and eddy are most often used interchangeably referring to the same phenomenon – understood in different contexts – turbulence in contexts of time, and eddy in contexts of space.
What are the sources of turbulence? The turbulent eddies originate from the interactions between two layers speeding relative to each other. This applies to speeding fluid layers as well as to fluids speeding past a solid boundary. As water speeds past the bottom irregularities of the bed both the layers are deformed. The deformation of the water layer gives birth to vertical (perpendicular to horizontal axis) eddies. The deformation of the bed adds to sediment transport if the bed comprises of erodible materials. Similar phenomenon occurs along the sides of a channel giving birth to the horizontal eddies (perpendicular to vertical axis). In addition, high turbulence is generated during impacts – of a solid object’s forceful entry into water – of breaking and plunging waves – and of hydraulic jumps.   
What are the scales of turbulent eddies? It turns out that the smallest size of an eddy scales with the minuscule size associated with the fluid molecular viscosity. The largest size is the constraint of the solid boundary – for the vertical eddies it is the depth of water, and for the horizontal eddies it is the lateral extent of the water body. How does the eddy size translate to its period or frequency? Turbulent eddies are transported by the mean flow during which they undergo transformation. Therefore eddy periods relate directly to its size but reciprocally to the mean transportation velocity – meaning that high flow velocity could break down large eddies into smaller pieces.
.  .  .     
The existence of turbulent eddies can be seen in time-series measurements of instantaneous velocities, and can be separated as perturbation from the time-mean. The three terms – instantaneous, perturbation and time-mean require some attention, because the understanding of turbulence depends on how well we define them.
Instantaneous means sensing at any instant – in reality however a sensor or recorder placed at some place can only act at a certain interval, which depends on the configuration of the sampling device accounting for its frequency and storage capacity (for the Jamuna River investigation, 10 and 20 ADCP pings were averaged giving a sampling interval of 5.5 and 10.5 second, respectively). The smaller the sampling interval, the higher is the resolution of the collected data. Perturbation is simply the deviation of the individual measurements from the time-mean. How to define the length of time to define the mean – to separate the sustained mean speed from turbulent speeds? This is one of the main problems – because choosing a short or long time could give different values and meanings – and they have different uses. I will answer this question based on my paper, but before that let me try to clarify the understanding of turbulence one more time.  .  .  .               
Perhaps we know more about this phenomenon in terms of wind – as wind gusts. The gusts are wind turbulence – sudden rushes of wind in speed and direction. As one can imagine a wind gust is much more erratic, less coherent and faster than its cousin, the water turbulence – one reason being the fact that air density is about 1000 times less than the water density. The definition of averaging time has very serious consequences in designs of civil engineering structures. As a practical solution of useful significance, a 3-second averaged wind speed is defined as the gust – and this is the speed used to estimate wind forces on building according to major design codes. In ship motion analysis a 30-second averaged wind speed is found to be appropriate. In other applications, a 2 to 10 minutes averaged speed is used. I will come back to the rationale behind selecting such different averaging times in engineering applications at some other time – only noting for now that the referred wind speeds are assumed to be measured at 10 meter above surface.  
.  .  .           
What should be the averaging time for water turbulence? To answer it properly a new term has to be defined – and this is known as turbulence intensity or strength. The turbulence intensity (TI) is the root-mean-square of the velocity perturbation. One can show the TI as a function of the averaging time – and in most cases the TI reaches a stable state at and after a threshold averaging time is reached – which means that nothing more can be gained by increasing the averaging-time further. It turns out that a constant level of TI is reached at and above an averaging time of about 5 minutes. However this time depends on the eddy sizes – the larger the size of an eddy the longer is the requirement of the averaging time. A 10 to 15 minutes averaging time seems to be adequate for most eddy sizes; however smaller averaging times may prove adequate for smooth beds such as a lined channel and bed.
How do the eddies behave after being born near to the bed? It turns out that TI scales with another hydraulic parameter – the so-called bed shear (or friction) velocity. This is a conceptual term applied to characterize flow velocity close to the bed – and is related to the bottom shear stress and bed roughness (see the Resistance to Flow on the SCIENCE & TECHNOLOGY page; and Seabed Roughness). I will come back to explaining more of these at some other time – for now, let us try to see how the ratio of TI and bed shear velocity decays over the depth. It turns out that the strength of turbulence or TI decays exponentially away from the source of its origin – the bed. But first it reaches the peak at a height of about 5 to 10% of the depth from the zero at the bed, after that the decaying process begins upward in the water column. This TI peak is in the order of about 2.0 times higher than bed shear velocity.
How does the TI scale with the local mean flow velocity? The Jamuna River data indicates that the magnitude of TI is about 7 to 10% of the local time-mean flow velocity in the free-stream region, but increases to 11 to 23% in the wall region close to the bed. This positive correlation between TI and the mean velocity is very significant because it suggests that the higher the mean velocity, the higher is the turbulence. No wonder this is reflected in the Reynolds Number (Osborne Reynolds, 1842 – 1912) which uses the mean velocity as one of the parameters to classify flows as laminar (fluid layers are smooth and parallel) and turbulent.
.  .  .
The Reynolds Number is applicable for equal-density homogeneous flow – when it is stratified with a definable density gradient, a different criterion is required to indicate the status of layer stability, turbulence and mixing. This criterion – a dimensionless parameter is known as the Richardson Number (British mathematician and physicist, Lewis Fry Richardson, 1881 - 1953) – which is directly proportional to the density gradient but inversely proportional to the velocity gradient squared. It turns out that when the number is less than a threshold value of 0.25, the layered flow starts to become unstable.       
Well so far so good. Let me finish this piece by answering one more question – Why understanding turbulence is important? In terms of the most significant practical considerations, turbulence is responsible for transfer of momentum across the flow field – mixing and homogenizing fluid layers. The process of momentum transfer is known as turbulent or Reynolds Stress – and is the product of fluid density and the mean of the product of turbulent perturbations in different directions.
But this stress needs a more workable definition to be useful. It was none other than Boussinesq (Joseph Valentin Boussinesq, 1842 – 1929) who formulated, in analogous to the molecular viscous stress, the Reynolds Stress in terms of the mean velocity gradients. The coefficients of his formulations are known as eddy viscosity coefficient for flow momentum transfer, and eddy diffusivity coefficient for transport of dissolved substances. The ratio between these two coefficients is known as Prandtl Number (German physicist Ludwig Prandtl, 1875 – 1953) for heat transport and Schmidt Number (German engineer Ernst Heinrich Wilhelm Schmidt, 1892 – 1975) for mass transport.
Well there is more. I will touch upon another important aspect, but will come back to discussing details on these aspects at some other time. We have discussed dynamic equilibrium, water modeling and the Navier-Stokes (Claude-Louis Navier, 1785 – 1836; George Gabriel Stokes, 1819 – 1903) equation in previous pieces. The Navier-Stokes equation truly represents an instantaneous flow field. In practice, measurements and modeling of instantaneous flows are not realistic. Therefore the equation must be translated to represent the mean quantities – yielding the so-called Reynolds Averaged Navier-Stokes (RANS) equation. The Boussinesq formulation and others come in handy to define the turbulence closure terms in the RANS equation. The others include: the mixing length concept, the kinetic energy-dissipation rate concept, and the mixing length formulation in terms of a coefficient and the model grid spacing. 

.  .  .  .  .

- by Dr. Dilip K. Barua, 24 November 2016 

---