 1. Waves Intro
In this piece let us attempt to see more of the Ocean Waves – the spectrum – and how to describe it. The wind generated ocean waves are described by many names – Sea State (sea surface undulations in a storm area) – Random Waves (waves with no apparent systematic pattern) – Irregular Waves (waves with no easily identifiable wave form). The relevance of the last two terms becomes evident when one examines a wave train individually – wave-by-wave. But with the introduction of the signal processing routine – the Fast Fourier Transform (FFT) since 1965 (J. W. Cooley and J. W. Tukey), and its application in digital processing has led to efficiency in wave studies – yielding a new term and meaning – and this term is Spectral Waves. Let us try to see what it means. . . . 2. Analyzing Waves Again, literature is full of materials on the subject but perhaps the Coastal Engineering Manual (CEM) of USACE (United States Army Corps of Engineers) is adequate for most purposes. Parts of this piece will also be based on three of my publications:
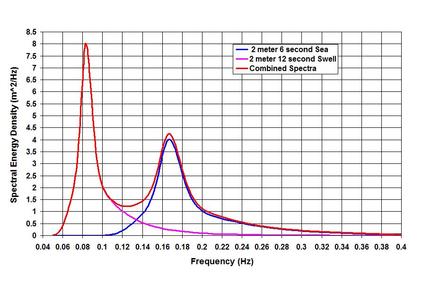
It was H.U. Sverdrup and W.H. Munk who answered the questions first in 1947 after World War II. They realized that it was necessary to solve a technicality first – should the wave height be measured from the trough to the following crest or from the crest to the following trough? The first approach is known as the zero-downcrossing method (starting from the point where water level starts crossing the still water line downward), and the second as the zero-upcrossing method. Because of the irregularity, the two methods do not yield identical results individually, but in aggregate, for let us say 1000 waves; both the methods yield nearly the same results. The authors have also realized that the mean wave height of the group may underestimate the group’s energy and effective forces. Therefore they have defined a very important parameter that continues to shape the meaning of the wave group in coastal engineering. This parameter is known as the significant wave height, Hs or H_1/3 – the average of the highest one-third of the wave group. Another important characteristic was observed by M.S. Longuet-Higgins in 1952. He found out that the frequency distributions followed certain patterns – the water levels as Gaussian Distribution (a symmetric distribution about the mean), and the wave heights as the Rayleigh (named after British physicist John William Strutt known as Lord Rayleigh, 1842 -1919) Distribution. The latter is a skewed distribution where the mean, median and mode do not coincide. The fitting to a known distribution was good news because it allowed scientists and engineers to define some useful parameters. For example, in a situation where 1000 waves are considered, if Hs = 1.0 meter, the maximum is 1.88 meter, the mean is 0.63 meter. Two more parameters are also important – the root-mean-square, Hrms = 0.71 meter often used for estimating sand transport; and the average of the highest 10th percentile, H_1/10 = 1.27 meter often used for determining wave forces on structures. How about the wave period distribution? The answer to the question by M.S. Longuet-Higgins in 1962 showed that wave periods followed Gaussian Distribution. However in 1969 C.L. Bretschneider showed that the squares of the period followed Rayleigh Distribution. The problem was further refined by S.K. Chakrabarti and R.P. Cooley in 1977. Let us try to see it more when discussing the wave spectra. One more thing before we move on to discussing the Spectral Waves. We have tried to see in the Duality and Multiplicity in Nature and Ocean Waves pieces on the NATURE page, and in the Transformation of Waves piece on the SCIENCE & TECHNOLOGY page that most natural waves are spectromatic and asymmetric starting from the time they are born. The closest approximation to the monochromatic and symmetric waves is the deep-water swells that have traveled from the storm area far into tranquil sea water. One experiences long crested (crest is relatively long perpendicular to the direction of wave propagation) swells in the sea where there are no winds to cause them. . . . 3. Spectral Waves 3.1 Long Wave Spectra How a long wave like tide is described in spectral terms? Tidal analyses and predictions are mostly based on spectral decomposition and superposition. The processes of decomposition by Fourier (French mathematician and physicist Jean-Baptiste Joseph Fourier, 1768 – 1830) and Harmonic analyses allow scientists to resolve the tidal wave to find the amplitude and phase of the contributing frequencies – those responsible for generation – as well as those developed by nonlinear interactions within the basin (e.g. my 1991 COPEDEC-PIANC paper: Tidal observations and spectral analyses of water level data in the mouth of the Ganges-Brahmaputra-Meghna river system). The decomposed parameters are then superimposed to predict tide by taking account of the constituent speed, annual nodal factor, astronomical argument etc. If presented as a spectrograph, it can be seen that most of the tidal energy is concentrated in the Semi-diurnal Principal Lunar Constituent. The reason for highlighting the spectral treatment of tide is to show the difference of it from the spectral description of wind waves. In the spectral treatment of wind waves, individual waves are not resolved and decomposed (although they can be analyzed as such like the Boussinesq modeling, Joseph Valentin Boussinesq, 1842 – 1929) to identify wave phases like tidal analysis. Instead time-series water surface elevations about a datum (such as the Still Water Level) are treated as signals by subjecting them to FFT analysis to translate the time-series into the frequency series of elevation variance – the energy density. While doing so, a cut-off frequency or Nyquist (Harry Nyquist, Swedish-American electronic engineer, 1889-1976) frequency is defined to indicate that the measured water levels cannot be resolved below twice the sampling interval. This treatment of water levels as a function of frequency is a simplification of the true nature of ocean waves – and is termed as one-dimensional spectrum. In reality ocean waves are also a function of direction – giving rise to the term directional spectrum (e.g. L.H. Holthuijsen in 1983). What we have discussed so far is the analysis of measured waves depicted in a spectrograph. How to model it to be useful for forecast? Many measured spectra hardly follow a definite pattern, but that did not stop investigators to model them. They proposed the so-called parametric empirical models to best describe the measured spectrum. Because of this approach, a certain model may not be representative for all water areas. Let me outline some of them briefly in this piece, I intend to talk more about them in the SCIENCE & TECHNOLOGY page at some other time. . . . 3.2 Short Wave Spectra As a forecasting tool, most of the models relate the spectrum to the wind speed, fetch (the distance along the wind direction from the shore to the point of interest) and storm duration (the duration of storm with a relatively unchanged sustained wind speed). Perhaps the 2-parameter spectrum proposed by C.L. Bretschneider in a paper in 1959 was the first of its kind. The paper by W.J. Pierson and L. Moskowitz in 1964 set the stage for describing the single-parameter wave spectrum for a fully developed sea state. In 1973, a 5-parameter spectrum known as JONSWAP (Joint North Sea Wave Project) spectrum was proposed by Hasselmann and others. It became popular as a forecasting tool for fetch-limited (when the storm duration is higher than a threshold that depends on the wind speed and fetch) conditions. Most of the proposed spectra are single peaked, which means if a wave field represents both wind waves and swells, the representation will not be accurate. In the single-peaked spectrum, the peak frequency or reciprocally the peak period Tp is defined as the period of the highest wave energy of the spectrum. On the question of double peaks, M.K. Ochi and E.N. Hubble came to the rescue in 1976 by proposing a 6-parameter spectrum that could describe both wind wave and swell spectra. To illustrate the nature, I have included an image of JONSWAP spectra – for peaks representing a 6-second (0.17 Hertz) sea and a 12-second (0.08 Hertz) swell, and the combined spectrum. Now that we have defined Tp and have some ideas about the wave period distribution, let us attempt to see how different wave periods in the distribution relate to each other. Again for about 1000 waves, if the Tp is 10 second, the zero-upcrossing period is 7.1 second, the significant wave period is 9.5 second, and the mean wave period is 7.7 second. Well so far so good, and I like to leave it at this for now. Sorry that the piece is steeped with technical terms and references – but unfortunately that is how the topic is. Yet many more investigators deserve credit but could not be highlighted in this short piece. Many of the proposed spectra are reviewed by Goda (Yoshima Goda, 1935 – 2012) in 2000, and also briefly in my Encyclopedia article in 2005 (the 2017 update). Before finishing, I like to touch upon three more aspects – the relation between Hs and the spectral determination of this parameter, the relationship between wave height and period, and the spectral evolution of waves. The significant wave height in a spectral approach, symbolized as Hmo or the zero-th moment is determined as 4 times the square root of the area under the spectrum. It turns out Hs and Hmo are not identical in shallow water, as well as in the cases of long-period waves. In both the cases Hs registers higher value than Hmo. The relationship between wave height and wave period is not unique – which means that a wave of the same height could exist both in high and low periods, or as a rephrase a wave of the same period could exist both in high and low heights. It becomes clear when one develops a joint frequency scatter of wave heights and periods. It turns out that a relationship could be established if one takes account of the wave steepness (ratio between wave height and local wave length). In my 2015 paper, I have proposed a relation that shows the wave period as a function of the square root of the wave height and reciprocal of the wave steepness. How does a wind generated wave-spectrum evolve over time as it propagates? I have addressed the question somewhat in the Transformation of Waves piece. Apart from the dispersion and separation of the long-period waves from the group, spectral evolution occurs through the wave to wave interactions. In deep-water, the evolution process known as the Quadruplet, accounts for spreading out the energy in both ways – towards the higher and lower frequencies, and also in directions (which means that the spectral peakedness flattens out). While spreading out of the peak energy occurs in deep-water, in the shallow refraction zone the wave to wave interactions result in a one way process known as the Triad – the transfer of the peak energy to the high frequencies (or low periods). Perhaps this process results in a spectral evolution that approaches the specter of a solitary monochromatic wave in very shallow water. . . . . . - by Dr. Dilip K. Barua, 27 October 2016
0 Comments
1. Intro
After the piece on Linear Waves, it only makes sense that I start this piece talking about Nonlinear Waves – from symmetry to asymmetry – from the processes of a zero residual to the complicacy of residuals. The nonlinearity is the characteristic signature of shallow water waves – and is also a recognizable feature of spectral wind waves that go through the nonlinear processes of interactions and high steepness. We have identified in earlier pieces that the single most important parameter, the Ursell Number, U = HL^2/d^3 (H is wave height, L is local wave length and d is local water depth) characterizes a wave as asymmetric or nonlinear, when U is greater than 5.0. The Ursell Number is universally applicable to all oscillatory flows, whether they are a short wave (like wind wave and swell) or a long wave (like tsunami, storm surge and tide). Some of the materials covered in this piece on tidal nonlinearity are taken from my Ph.D. Dissertation (Dynamics of Coastal Circulation and Sediment Transport in the Coastal Ocean off the Ganges-Brahmaputra River Mouth, the University of South Carolina, 1992) along with two of my relevant publications:
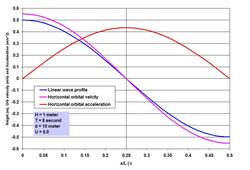
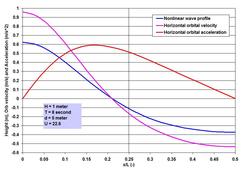
Many investigators are credited with developing the nonlinear wave theories. To name some, perhaps we can start with Stokes (British mathematician George Gabriel Stokes, 1819 – 1903; Stokes Finite Amplitude Wave Theory), J. S. Russell and J. McCowan (Solitary Wave Theory), D. J. Korteweg and D. de Vries (Cnoidal Wave Theory), Robert G. Dean (Stream Function Theory) and J. D. Fenton (Fourier Series Theory). Many more investigators were involved in expanding and refining the theories, some names include R. L. Weigel, L. Skjelbreia, R. A. Dalrymple and J. R. Chaplin. . . . 2. Nonlinear Wave Kinematics With this brief introduction, let us now try to understand what nonlinearity means exactly. To illustrate it, I have included two images showing the wave profile, surface horizontal orbital velocity and acceleration for the same 1 meter high 8 second wave, I have shown in the Linear Waves piece. Depicting the parameters for half the wave length, it is immediately clear how the crest is heightened and the trough is flattened when the wave propagates straight shoreward from U = 5.0 to 22.6 (note that 22.6 is near the threshold at which waves can also be treated as Cnoidal). Horizontal water particle velocity has nearly doubled at the crest with the reduction at the trough. For acceleration, the change is not only in the increase in magnitude but also in the phase shift from the symmetry at quarter wave length to the forward skewed distribution. Even this nonlinearity as complicated as it is – is a simplification of the reality because more processes such as reflection and interactions play a role in defining the wave evolution in the nearshore region. We have talked about Stokes Drift in the Transformation of Waves piece on the SCIENCE & TECHNOLOGY page. Stokes Drift or mass transport horizontal velocity represents a nonlinear residual in the direction of wave propagation, and is about one order less in magnitude than the horizontal orbital velocity. For the nonlinear wave at U = 22.6, while the peak surface horizontal orbital velocity is 0.96 meter per second, the drift is roughly about 5 centimeter per second. This drift may seem very small, but a particle traveling at this speed will travel to 180 meter in an hour. Before going further, an important parameter – the local wave length L needs some attention. We have seen in the Linear Waves piece that determining L iteratively has become easy with the modern computing systems, or by applying the Hunt (H. N. Hunt, 1979) method. However as waves become nonlinear, the wave length starts to deviate from the L determined by Linear Wave Theory. It turns out that at U > 5.0, the deviation becomes increasingly larger as U increases, but remains within about 10%. Why understanding the nonlinear wave phenomenon is important? A simple answer to the question is that the nonlinearity of oscillatory flows is responsible for many processes that define a coastal system behavior and characteristics, and in the behaviors of hydrodynamic loading on, and stability of in-water and waterfront structures. Let me try to outline three of them briefly. . . . 3. Consequences of Wave Asymmetry and Nonlinearity The first is the effects of the increase and phase-shift of the orbital velocity and acceleration as shown in the images. These processes have significant implications for wave-induced drag, lift and inertial Morison forces (J. R. Morison and others, 1950; forces on slender members) on coastal and port structures. Horizontal drag and inertial forces are relevant in terms of the maximums; therefore as the maximums increase so do the forces. The pieces Characterizing Wave Asymmetry and Wave Forces on Slender Structures discusses such aspects. When I stated about the phase-shifts and the relevance of maximums, did anyone notice a contradiction in my statement of Morison forces? Well there is one – the contradiction is due to one of the methods engineers often apply to accommodate some maximums – however unscientific the method may appear – for a conservative and safe design by implanting the so-called Hidden Factor of Safety. Let us discuss more of this aspect in the SCIENCE & TECHNOLOGY page along with my ISOPE paper (Wave Loads on Piles – Spectral Versus Monochromatic Approach, 2008). How does one define the increased nonlinear maximums in terms of asymmetry? Some of my works (not published) indicate that one could relate the amplitude asymmetry of velocity and acceleration in terms of U. Once such a relation is established, it becomes rather easy to determine the nonlinear Morison forces. The second is the effect of the nonlinearity as it interacts with the seabed – the processes generate enhanced turbulence, and when the threshold is exceeded, they are responsible for erosion and resuspension of sediments. Depending on circumstances, nonlinearity is responsible for residual transports toward the onshore, offshore or longshore directions. How to characterize the residuals? I will try to answer this question based on my Ph.D. works and the two relevant publications already mentioned. This will be done for tide, tidal currents and Suspended Sediment (mostly fine sediments that are kept in suspension in the water column by currents and turbulence) Concentrations (SSC). One method to indicate the residuals e.g. of to-and-fro tidal currents (currents are vector kinematics with both magnitude and direction) is to make vector addition of the individual measurements (such as hourly) – such a method immediately shows that a circle cannot be completed because of nonlinearity – and also due to the effects of other superimposed currents such as a river discharge or wind drift, if present. If seaward currents are high at river mouths, residuals are mostly seaward; on the other hand, in absence of a river current or wind drift, tidal asymmetry is responsible for landward transport, and accumulation of fine sediments in tidal flats. These effects of varying superimposed currents and asymmetries often stratify a shallow and wide coastal system horizontally – the coastal ocean off the Ganges-Brahmaputra system is one of such systems. The residual current vectors are a good indicator of, and to where suspended fine (mostly silt and clay sized particles) sediments or water-borne contaminants are likely to end up. The combined tidal current and SSC measurements over time and over the depth can be analyzed applying a procedure known as the linear perturbation principle – a method of vector averaging and identifications of perturbations from the mean. The procedure yields some 5 terms accounting for non-tidal actions, and for the asymmetries of tide, tidal currents and the hysteresis of SSC over time and over the depth. Such methods of separating the components are very useful to provide valuable insights into the identification of processes responsible for certain actions and behaviors. The third is on the most dynamic region of wave action – the surf zone. This is the region where the wave nonlinearity reaches its ultimate stage by breaking as the horizontal wave orbital velocity overtakes the celerity. The breaker line or rather the breaker zone is not fixed, because the breaking depth together with the effects of rising and falling tides is related to the changing wave height. The transformation of the near-oscillatory waves into the near-translatory water motion by wave breaking and energy dissipation is the most recognizable process in this zone. Let us try to see more of it at some other time. . . . . . - by Dr. Dilip K. Barua, 20 October 2016 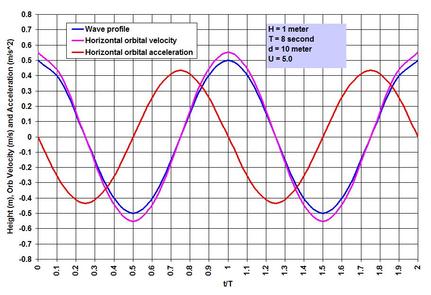 1. Intro
Let me begin by saying that linear waves rarely exist in a natural ocean wave environment, yet the simplification and approximation applied to treat waves as such are very useful for many purposes. These purposes are well served especially for cases in deep-water conditions (where the local depth is greater than half of the local wave length). The simplified and approximated wave is known variously as Linear Wave, Small Amplitude Wave, 1st Order Wave or Airy Wave in honor of George Biddell Airy (1801 – 1892), who was attributed to have derived it first. All natural water waves are gravitational waves – not in a sense that they are generated by gravity, but rather by the fact that gravity is the restoring force – in an equilibrium process between the disturbing and restoring forces. Literature is full of materials dealing with the Linear Wave Theory. Perhaps the Coastal Engineering Manual (CEM) series produced by USACE is adequate to satisfy many curiosities about ocean waves. In the Ocean Waves piece on this page, and in the Transformation of Waves blog on the SCIENCE & TECHNOLOGY page we have talked about the nature of ocean waves and the transformation processes in plain and poetic terms. Before going further into discussing more of the wave aspects, perhaps it is necessary to introduce the simplicity of linear waves first. Let me try to do that in this piece. What are the approximations and simplifications applied to derive it? A linear wave is nothing but the representation of a circle – in the symmetry of a sinusoidal or harmonic wave. This is obtained by Airy solving the unsteady Bernoulli (Daniel Bernoulli, 1700 – 1782) equation to the 1st order. His solution is based on four major assumptions, that the wave motion is: (1) irrotational (no shearing between layers of motion), (2) progressive (continuous in motion in the direction of propagation without reflection), (3) very small in amplitude compared to the length of the wave, and (4) the motion is 2-dimensional confined within a slice of water cut to the depth along its length of propagation. When the first three assumptions are invalid, the wave loses its symmetry and a nonlinear wave theory applies. . . . 2. Characteristics of a Linear Wave What are the fundamental characteristics of a linear wave? From previous discussions we have learned that a wave can be described by 3 fundamental parameters: wave height H (the height from trough to crest), local wave length L or wave period T (measured simply from crest to crest), and the local still water depth d. As we have seen earlier, a very useful parameter proposed by Fritz Joseph Ursell (1923 – 2012) uses these three parameters to indicate whether waves can be approximated by the 1st order processes of the Linear Wave Theory. This parameter known as the Ursell Number describes a threshold combining the two ratios H/d and d/L, and is given by U = HL^2/d^3. It turns out that for all practical purposes, waves can be assumed to be symmetric or linear, when U is equal to or less than 5.0. In addition, two more parameters appear in all the terms describing the wave properties in time and space. The first, useful to describe the wave in time, is known as the wave angular frequency and is given as a ratio between 2*pi and T. The second, useful to describe the wave in space, is known as the wave number and is given as a ratio between 2*pi and L. The Greek symbol pi is a universal constant defining a circle and represents the ratio between the circle perimeter and diameter. The wave length L is a unique function of T in deep water, but in shallower water it becomes dependent on depth d as well. Except in very shallow water, it becomes rather cumbersome to determine the local wave length because L appears on both sides of the equation. The past coastal engineering literature had elaborate graphical methods to facilitate local wave length computations. But with the arrival of digital computation, iteration has become easy to determine it exactly. However a simple method proposed by Hunt in 1979 is incredibly accurate very close to the exact iterative solution. . . . 3. Linear Wave Kinematics Let us try to chalk out some of the salient linear wave characteristics in order to understand the simplicity of it better. To help us in this regard, I have included an image showing the wave profile and surface wave kinematics for a 1 meter high 8 second wave in 10 meter of water depth. The horizontal axis of this image is time normalized by the wave period. Wave celerity (speed of the propagating energy) is a function of wave period T and local water depth d. It is independent of wave height H, except in spectral waves, where H and T are positively correlated, albeit weakly. We will talk more about it at some other time. Wave kinematics (velocity and acceleration) equations may appear intimidating, but can simply be identified as the product of three parameters: an amplitude, a periodic sine or cosine function and a hyperbolic factor accounting for asymptotic reduction of wave kinematics from surface to the bottom. Orbital wave particle velocity is directly proportional to H, but inversely proportional to T. The horizontal and vertical velocities are out of phase by 90 degrees – which means that while the horizontal velocity is forward at the wave crest and backward at the wave trough, the vertical velocity is upward at the 1st quarter and downward at the 3rd quarter. Surfers and wave-swimmers know and feel these effects of velocities. Orbital wave particle acceleration is directly proportional to H but inversely proportional to T^2. Similar to the velocity, horizontal and vertical accelerations are out of phase by 90 degrees. Horizontal accelerations are zero both at the crest and trough, but forward at the 1st quarter and backward at the 3rd quarter. The vertical accelerations are downward at the crest, upward at the trough, and zero at both 1st and 3rd quarters. . . . 4. Wave Energy and Power We have talked about external energies generating waves and propelling them to the destiny of transporting the gained energy forward. How much energy does a wave carry? What is its power? One simple way to answer these questions is by the Linear Wave Theory. Like all waters in motion, energy can be separated into two components – the potential energy and the kinetic energy. Potential energy is due to the displacement of water mass above still water level (SWL), and the kinetic energy is due to the water particle velocity. It turns out that the two components of the wave energy are equal to each other, and are proportional to H^2. This means that the energies of 1 and 2 meter high waves vary by 1 to 4. Wave energy is generally quoted as energy density, which refers to the energy per unit wave length. This means that a wave of the same height carries more total energy for a long period wave than a shorter one. The power is a vector term that works in the direction of wave propagation. Wave power is the product of energy density and celerity (or group celerity for a spectral wave). The wave power is also known as wave energy flux or wave action. The method of balancing the wave action lets one to determine the transformed and/or transmitted waves across varying depths or in situations of wave-structure interactions. . . . 5. Wave Radiation Stress and Momentum Flux There are two other important terms that require some attention – these are known as the radiation stress and momentum flux. Both of these horizontal forces in the direction of wave propagation are caused by the dynamic pressure and the pressure exerted by kinetic energy (also dynamic in nature). Radiation stress develops due to the excess pressure – and is due to wave nonlinearity. Let us talk about this some other time. Dynamic Pressure is the result of changing water surface elevation up and down of SWL – and is in phase with wave profile. What does this imply? The dynamic pressure implies that one feels excess pressure (compared to hydrostatic pressure) when under the wave crest and less or an uplift pressure under the trough. This process allows scientists to measure wave height by deploying subsurface pressure sensors. The concept of momentum flux has been proposed by Steven Hughes of USACE in 2003. The instantaneous value of this parameter is the summation of the horizontal dynamic pressure and the pressure induced by the kinetic energy. Among others, the momentum flux is very useful to assess wave interactions with intervening structures and depth changes. Well, these are some of the important aspects of linear waves in a nutshell. Let us finish this piece with a quote from Einstein (1879 – 1955): everything should be made as simple as possible, but no simpler. . . . Here is an anecdote to ponder: In the meantime the disciple went on a vacation – fully paid. The poor master also went on a vacation – but unpaid, and just in the neighborhood listening to the songs of life and Nature. . . . . . - by Dr. Dilip K. Barua, 13 October 2016 |
RSS Feed
