Linear Waves

1. Intro
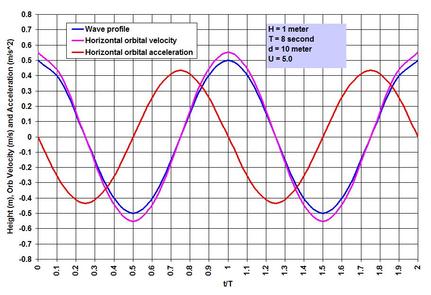
Let me begin by saying that linear waves rarely exist in a natural ocean wave environment, yet the simplification and approximation applied to treat waves as such are very useful for many purposes. These purposes are well served especially for cases in deep-water conditions (where the local depth is greater than half of the local wave length). The simplified and approximated wave is known variously as Linear Wave, Small Amplitude Wave, 1st Order Wave or Airy Wave in honor of George Biddell Airy (1801 – 1892), who was attributed to have derived it first. All natural water waves are gravitational waves – not in a sense that they are generated by gravity, but rather by the fact that gravity is the restoring force – in an equilibrium process between the disturbing and restoring forces.    
Literature is full of materials dealing with the Linear Wave Theory. Perhaps the Coastal Engineering Manual (CEM) series produced by USACE is adequate to satisfy many curiosities about ocean waves.   
In the Ocean Waves piece on this page, and in the Transformation of Waves blog on the SCIENCE & TECHNOLOGY page we have talked about the nature of ocean waves and the transformation processes in plain and poetic terms. Before going further into discussing more of the wave aspects, perhaps it is necessary to introduce the simplicity of linear waves first. Let me try to do that in this piece.
What are the approximations and simplifications applied to derive it? A linear wave is nothing but the representation of a circle – in the symmetry of a sinusoidal or harmonic wave. This is obtained by Airy solving the unsteady Bernoulli (Daniel Bernoulli, 1700 – 1782) equation to the 1st order. His solution is based on four major assumptions, that the wave motion is:
(1) irrotational (no shearing between layers of motion),
(2) progressive (continuous in motion in the direction of propagation without reflection),
(3) very small in amplitude compared to the length of the wave, and
(4) the motion is 2-dimensional confined within a slice of water cut to the depth along its length of propagation.
When the first three assumptions are invalid, the wave loses its symmetry and a nonlinear wave theory applies.
.  .  .
2. Characteristics of a Linear Wave
What are the fundamental characteristics of a linear wave? From previous discussions we have learned that a wave can be described by 3 fundamental parameters: wave height H (the height from trough to crest), local wave length L or wave period T (measured simply from crest to crest), and the local still water depth d. As we have seen earlier, a very useful parameter proposed by Fritz Joseph Ursell (1923 – 2012) uses these three parameters to indicate whether waves can be approximated by the 1st order processes of the Linear Wave Theory. This parameter known as the Ursell Number describes a threshold combining the two ratios H/d and d/L, and is given by U = HL^2/d^3. It turns out that for all practical purposes, waves can be assumed to be symmetric or linear, when U is equal to or less than 5.0.
In addition, two more parameters appear in all the terms describing the wave properties in time and space. The first, useful to describe the wave in time, is known as the wave angular frequency and is given as a ratio between 2*pi and T. The second, useful to describe the wave in space, is known as the wave number and is given as a ratio between 2*pi and L. The Greek symbol pi is a universal constant defining a circle and represents the ratio between the circle perimeter and diameter.
The wave length L is a unique function of T in deep water, but in shallower water it becomes dependent on depth d as well. Except in very shallow water, it becomes rather cumbersome to determine the local wave length because L appears on both sides of the equation. The past coastal engineering literature had elaborate graphical methods to facilitate local wave length computations. But with the arrival of digital computation, iteration has become easy to determine it exactly. However a simple method proposed by Hunt in 1979 is incredibly accurate very close to the exact iterative solution.
.  .  .
3. Linear Wave Kinematics
Let us try to chalk out some of the salient linear wave characteristics in order to understand the simplicity of it better. To help us in this regard, I have included an image showing the wave profile and surface wave kinematics for a 1 meter high 8 second wave in 10 meter of water depth. The horizontal axis of this image is time normalized by the wave period. 
Wave celerity (speed of the propagating energy) is a function of wave period T and local water depth d. It is independent of wave height H, except in spectral waves, where H and T are positively correlated, albeit weakly. We will talk more about it at some other time. 
Wave kinematics (velocity and acceleration) equations may appear intimidating, but can simply be identified as the product of three parameters: an amplitude, a periodic sine or cosine function and a hyperbolic factor accounting for asymptotic reduction of wave kinematics from surface to the bottom. 
Orbital wave particle velocity is directly proportional to H, but inversely proportional to T. The horizontal and vertical velocities are out of phase by 90 degrees – which means that while the horizontal velocity is forward at the wave crest and backward at the wave trough, the vertical velocity is upward at the 1st quarter and downward at the 3rd quarter. Surfers and wave-swimmers know and feel these effects of velocities.      
Orbital wave particle acceleration is directly proportional to H but inversely proportional to T^2. Similar to the velocity, horizontal and vertical accelerations are out of phase by 90 degrees. Horizontal accelerations are zero both at the crest and trough, but forward at the 1st quarter and backward at the 3rd quarter. The vertical accelerations are downward at the crest, upward at the trough, and zero at both 1st and 3rd quarters.
.  .  .
4. Wave Energy and Power
We have talked about external energies generating waves and propelling them to the destiny of transporting the gained energy forward. How much energy does a wave carry? What is its power? One simple way to answer these questions is by the Linear Wave Theory.
Like all waters in motion, energy can be separated into two components – the potential energy and the kinetic energy. Potential energy is due to the displacement of water mass above still water level (SWL), and the kinetic energy is due to the water particle velocity. It turns out that the two components of the wave energy are equal to each other, and are proportional to H^2. This means that the energies of 1 and 2 meter high waves vary by 1 to 4. Wave energy is generally quoted as energy density, which refers to the energy per unit wave length. This means that a wave of the same height carries more total energy for a long period wave than a shorter one.
The power is a vector term that works in the direction of wave propagation. Wave power is the product of energy density and celerity (or group celerity for a spectral wave). The wave power is also known as wave energy flux or wave action. The method of balancing the wave action lets one to determine the transformed and/or transmitted waves across varying depths or in situations of wave-structure interactions.
.  .  .
5. Wave Radiation Stress and Momentum Flux
There are two other important terms that require some attention – these are known as the radiation stress and momentum flux. Both of these horizontal forces in the direction of wave propagation are caused by the dynamic pressure and the pressure exerted by kinetic energy (also dynamic in nature). Radiation stress develops due to the excess pressure – and is due to wave nonlinearity. Let us talk about this some other time.
Dynamic Pressure is the result of changing water surface elevation up and down of SWL – and is in phase with wave profile. What does this imply? The dynamic pressure implies that one feels excess pressure (compared to hydrostatic pressure) when under the wave crest and less or an uplift pressure under the trough. This process allows scientists to measure wave height by deploying subsurface pressure sensors.
The concept of momentum flux has been proposed by Steven Hughes of USACE in 2003. The instantaneous value of this parameter is the summation of the horizontal dynamic pressure and the pressure induced by the kinetic energy. Among others, the momentum flux is very useful to assess wave interactions with intervening structures and depth changes.  
Well, these are some of the important aspects of linear waves in a nutshell. Let us finish this piece with a quote from Einstein (1879 – 1955): everything should be made as simple as possible, but no simpler.       
.  .  .                                        
Here is an anecdote to ponder:
In the meantime the disciple went on a vacation – fully paid. The poor master also went on a vacation – but unpaid, and just in the neighborhood listening to the songs of life and Nature. 

.  .  .  .  .

- by Dr. Dilip K. Barua, 13 October 2016

---