 1. Waves Intro
In this piece let us attempt to see more of the Ocean Waves – the spectrum – and how to describe it. The wind generated ocean waves are described by many names – Sea State (sea surface undulations in a storm area) – Random Waves (waves with no apparent systematic pattern) – Irregular Waves (waves with no easily identifiable wave form). The relevance of the last two terms becomes evident when one examines a wave train individually – wave-by-wave. But with the introduction of the signal processing routine – the Fast Fourier Transform (FFT) since 1965 (J. W. Cooley and J. W. Tukey), and its application in digital processing has led to efficiency in wave studies – yielding a new term and meaning – and this term is Spectral Waves. Let us try to see what it means. . . . 2. Analyzing Waves Again, literature is full of materials on the subject but perhaps the Coastal Engineering Manual (CEM) of USACE (United States Army Corps of Engineers) is adequate for most purposes. Parts of this piece will also be based on three of my publications:
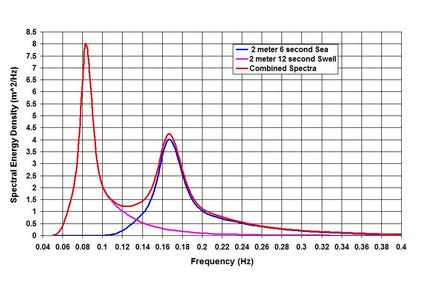
It was H.U. Sverdrup and W.H. Munk who answered the questions first in 1947 after World War II. They realized that it was necessary to solve a technicality first – should the wave height be measured from the trough to the following crest or from the crest to the following trough? The first approach is known as the zero-downcrossing method (starting from the point where water level starts crossing the still water line downward), and the second as the zero-upcrossing method. Because of the irregularity, the two methods do not yield identical results individually, but in aggregate, for let us say 1000 waves; both the methods yield nearly the same results. The authors have also realized that the mean wave height of the group may underestimate the group’s energy and effective forces. Therefore they have defined a very important parameter that continues to shape the meaning of the wave group in coastal engineering. This parameter is known as the significant wave height, Hs or H_1/3 – the average of the highest one-third of the wave group. Another important characteristic was observed by M.S. Longuet-Higgins in 1952. He found out that the frequency distributions followed certain patterns – the water levels as Gaussian Distribution (a symmetric distribution about the mean), and the wave heights as the Rayleigh (named after British physicist John William Strutt known as Lord Rayleigh, 1842 -1919) Distribution. The latter is a skewed distribution where the mean, median and mode do not coincide. The fitting to a known distribution was good news because it allowed scientists and engineers to define some useful parameters. For example, in a situation where 1000 waves are considered, if Hs = 1.0 meter, the maximum is 1.88 meter, the mean is 0.63 meter. Two more parameters are also important – the root-mean-square, Hrms = 0.71 meter often used for estimating sand transport; and the average of the highest 10th percentile, H_1/10 = 1.27 meter often used for determining wave forces on structures. How about the wave period distribution? The answer to the question by M.S. Longuet-Higgins in 1962 showed that wave periods followed Gaussian Distribution. However in 1969 C.L. Bretschneider showed that the squares of the period followed Rayleigh Distribution. The problem was further refined by S.K. Chakrabarti and R.P. Cooley in 1977. Let us try to see it more when discussing the wave spectra. One more thing before we move on to discussing the Spectral Waves. We have tried to see in the Duality and Multiplicity in Nature and Ocean Waves pieces on the NATURE page, and in the Transformation of Waves piece on the SCIENCE & TECHNOLOGY page that most natural waves are spectromatic and asymmetric starting from the time they are born. The closest approximation to the monochromatic and symmetric waves is the deep-water swells that have traveled from the storm area far into tranquil sea water. One experiences long crested (crest is relatively long perpendicular to the direction of wave propagation) swells in the sea where there are no winds to cause them. . . . 3. Spectral Waves 3.1 Long Wave Spectra How a long wave like tide is described in spectral terms? Tidal analyses and predictions are mostly based on spectral decomposition and superposition. The processes of decomposition by Fourier (French mathematician and physicist Jean-Baptiste Joseph Fourier, 1768 – 1830) and Harmonic analyses allow scientists to resolve the tidal wave to find the amplitude and phase of the contributing frequencies – those responsible for generation – as well as those developed by nonlinear interactions within the basin (e.g. my 1991 COPEDEC-PIANC paper: Tidal observations and spectral analyses of water level data in the mouth of the Ganges-Brahmaputra-Meghna river system). The decomposed parameters are then superimposed to predict tide by taking account of the constituent speed, annual nodal factor, astronomical argument etc. If presented as a spectrograph, it can be seen that most of the tidal energy is concentrated in the Semi-diurnal Principal Lunar Constituent. The reason for highlighting the spectral treatment of tide is to show the difference of it from the spectral description of wind waves. In the spectral treatment of wind waves, individual waves are not resolved and decomposed (although they can be analyzed as such like the Boussinesq modeling, Joseph Valentin Boussinesq, 1842 – 1929) to identify wave phases like tidal analysis. Instead time-series water surface elevations about a datum (such as the Still Water Level) are treated as signals by subjecting them to FFT analysis to translate the time-series into the frequency series of elevation variance – the energy density. While doing so, a cut-off frequency or Nyquist (Harry Nyquist, Swedish-American electronic engineer, 1889-1976) frequency is defined to indicate that the measured water levels cannot be resolved below twice the sampling interval. This treatment of water levels as a function of frequency is a simplification of the true nature of ocean waves – and is termed as one-dimensional spectrum. In reality ocean waves are also a function of direction – giving rise to the term directional spectrum (e.g. L.H. Holthuijsen in 1983). What we have discussed so far is the analysis of measured waves depicted in a spectrograph. How to model it to be useful for forecast? Many measured spectra hardly follow a definite pattern, but that did not stop investigators to model them. They proposed the so-called parametric empirical models to best describe the measured spectrum. Because of this approach, a certain model may not be representative for all water areas. Let me outline some of them briefly in this piece, I intend to talk more about them in the SCIENCE & TECHNOLOGY page at some other time. . . . 3.2 Short Wave Spectra As a forecasting tool, most of the models relate the spectrum to the wind speed, fetch (the distance along the wind direction from the shore to the point of interest) and storm duration (the duration of storm with a relatively unchanged sustained wind speed). Perhaps the 2-parameter spectrum proposed by C.L. Bretschneider in a paper in 1959 was the first of its kind. The paper by W.J. Pierson and L. Moskowitz in 1964 set the stage for describing the single-parameter wave spectrum for a fully developed sea state. In 1973, a 5-parameter spectrum known as JONSWAP (Joint North Sea Wave Project) spectrum was proposed by Hasselmann and others. It became popular as a forecasting tool for fetch-limited (when the storm duration is higher than a threshold that depends on the wind speed and fetch) conditions. Most of the proposed spectra are single peaked, which means if a wave field represents both wind waves and swells, the representation will not be accurate. In the single-peaked spectrum, the peak frequency or reciprocally the peak period Tp is defined as the period of the highest wave energy of the spectrum. On the question of double peaks, M.K. Ochi and E.N. Hubble came to the rescue in 1976 by proposing a 6-parameter spectrum that could describe both wind wave and swell spectra. To illustrate the nature, I have included an image of JONSWAP spectra – for peaks representing a 6-second (0.17 Hertz) sea and a 12-second (0.08 Hertz) swell, and the combined spectrum. Now that we have defined Tp and have some ideas about the wave period distribution, let us attempt to see how different wave periods in the distribution relate to each other. Again for about 1000 waves, if the Tp is 10 second, the zero-upcrossing period is 7.1 second, the significant wave period is 9.5 second, and the mean wave period is 7.7 second. Well so far so good, and I like to leave it at this for now. Sorry that the piece is steeped with technical terms and references – but unfortunately that is how the topic is. Yet many more investigators deserve credit but could not be highlighted in this short piece. Many of the proposed spectra are reviewed by Goda (Yoshima Goda, 1935 – 2012) in 2000, and also briefly in my Encyclopedia article in 2005 (the 2017 update). Before finishing, I like to touch upon three more aspects – the relation between Hs and the spectral determination of this parameter, the relationship between wave height and period, and the spectral evolution of waves. The significant wave height in a spectral approach, symbolized as Hmo or the zero-th moment is determined as 4 times the square root of the area under the spectrum. It turns out Hs and Hmo are not identical in shallow water, as well as in the cases of long-period waves. In both the cases Hs registers higher value than Hmo. The relationship between wave height and wave period is not unique – which means that a wave of the same height could exist both in high and low periods, or as a rephrase a wave of the same period could exist both in high and low heights. It becomes clear when one develops a joint frequency scatter of wave heights and periods. It turns out that a relationship could be established if one takes account of the wave steepness (ratio between wave height and local wave length). In my 2015 paper, I have proposed a relation that shows the wave period as a function of the square root of the wave height and reciprocal of the wave steepness. How does a wind generated wave-spectrum evolve over time as it propagates? I have addressed the question somewhat in the Transformation of Waves piece. Apart from the dispersion and separation of the long-period waves from the group, spectral evolution occurs through the wave to wave interactions. In deep-water, the evolution process known as the Quadruplet, accounts for spreading out the energy in both ways – towards the higher and lower frequencies, and also in directions (which means that the spectral peakedness flattens out). While spreading out of the peak energy occurs in deep-water, in the shallow refraction zone the wave to wave interactions result in a one way process known as the Triad – the transfer of the peak energy to the high frequencies (or low periods). Perhaps this process results in a spectral evolution that approaches the specter of a solitary monochromatic wave in very shallow water. . . . . . - by Dr. Dilip K. Barua, 27 October 2016
0 Comments
Leave a Reply. |
RSS Feed
