 When I started writing this piece, I thought of a title like: The Hydraulics of Sediment Motion. Well this would not have been right – would it? The reason is that sediments need energy from water motion – they do not have any to propel themselves. They need local hydrodynamic energy to be picked up from the bed – to be transported hopping up and down near the bed – and to be carried while in suspension in the water column. Because of this necessity, sediment transport processes are alternatively referred to as sediment load dynamics. The loads are carried by the water motion as long as the local transport power exceeds the downward gravitational pull acting on the sediment particles. Before moving further one needs to clarify a distinction however. This distinction between non-cohesive and cohesive sediments and transports is based on the relative dominance of gravitational and electrochemical forces. The non-cohesive texture is dominated by individual sand grains (> 0.063 mm) – their settling and transport are controlled by gravity. For silt (0.063 mm > silt > 0.004 mm) and clay (< 0.004 mm) sized particles, on the other hand, the electrochemical processes (function of mineralogy and water chemistry – salinity and temperature) of aggregation and flocculation play a dominant role in binding individual particles loosely together. My own experiments {Discussion of ‘Management of Fluid Mud in Estuaries, Bays, and Lakes. I: Present State of Understanding on Character and Behavior’ ASCE Journal of Hydraulic Engineering, 2008} throw some insights on this. Analysis of mud samples (median diameter varying from 0.006 mm to 0.011 mm) consisting of 14.9% to 34.1% clay content (characterized by clay-size mineralogy: 52% illite, 23% kaolinite, 15% smectite, and 10% others) shows exponentially decreasing suspended sediment concentration with increasing salinity – an indication of enhanced salinity-induced flocculation and settling. Once deposited, the cohesive sediments form a loosely packed easily erodible fluid-mud layer, which becomes hard mud through the slow processes of consolidation. The transport of cohesive sediments is often termed as wash load transport – as opposed to bed-material transport – with the arguments that their concentration and transport are independent of local hydrodynamics and bed-material composition. As a blanket classification, all silt and clay sized particles (< 0.063 mm) are considered as wash load. In one of my IEB papers (Sediment Transport in Suspension: an Examination of the Difference between Bed-material Load and Wash Load, IEB 1995), I argued against this blanket classification and showed from field measurements that the classification should instead be based on local hydrodynamic energy criteria proposed by Vlugter (1941) and Bagnold (1962). . . . This piece is about non-cohesive sediment transport dynamics in alluvial coastal waters. This type of transport is notoriously erratic due to the continuous interactions between gravity, and flow turbulence – more vigorous within the boundary layer close to the bed than in layers upward in the water column (see the Turbulence piece on this page and my IAHR paper published by Taylor & Francis – where it is shown that bed-turbulence reaches peak at 5% to 10% of depth above the bed). The transport in coastal waters can be distinguished as two basic types: the transport within the wave breaking surf zone is highly driven by breaking wave turbulence – liquefied and suspended by turbulence, the sediments are transported in this zone by longshore and cross-shore currents – by undertow offshore currents, and by longshore currents generated by obliquely breaking waves. See more in The Surf Zone. Outside the surf zone, sediment transport dynamics are dominated by processes similar to steady currents – but in somewhat different fashions accounting for nearbed wave orbital velocity, friction factor, and other currents generated by tide, tsunami and storm surge. The transports within the surf zone are not covered in this piece – hope to come back to this at some other time. This piece is on bed-material transport and processes outside the surf zone. There are colossal amount of literature on bed-material sediment transports – to the extent of some confusion. The reason for so much attention and investments is that the sedimentation management and engineering comprise a very complicated problem – not only because of the complicated theories and relations, but also because of the real-world hydrodynamic actions in varied frequencies and directions and corresponding responses of the alluvial seabed. The result is that although there are general agreements on the nature of dependent variables, very few relations agree in terms of inter-relationships, and in predictions of transport quantities. So it is no surprising that the disagreement in predicted transports can vary by as much as ± 100%. Let us attempt to understand all this in a nutshell – and as we move along, references used for this piece will come to light – including some of my published works. . . . What must one look for in studying sediment transport dynamics? Here is a brief outline.
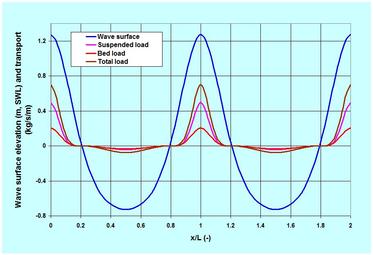
. . . Nearbed Fluid Forcing and Bed Resistance. To describe this aspect of the transport dynamics, I will mainly use materials from my 2017 published chapter in the Encyclopedia of Coastal Science (Seabed Roughness of Coastal Waters). In an oscillatory environment of coastal waters, the nearbed fluid forcing or bed-shear stress is formulated in terms of the quadratic friction law, which is rooted in Bernoulli (Daniel Bernoulli, 1700 – 1782) theorem. The bed resistance in the friction law is expressed in terms of a drag coefficient (or its equivalent: Chezy C, Manning n and Darcy-Weisbach f) in currents, and a friction factor (fw) in waves – its value depending on the seabed sediment texture and bedforms. The quadratic friction law says that the bed-shear stress is the product of a friction factor, fluid density and the nearbed orbital velocity squared. As an example: for a low-steepness, 2-meter high 12-second wave (wave steepness = 0.017) at 10 meter water depth on 0.5 mm coarse-sand seabed, the peak wave friction factor is 0.0089 – exerting an equivalent peak wave-forced bed-shear velocity of 0.079 m/s. As the Ursell Number (U = 26.8) is very high – Stokes 5th order nonlinear wave theory is applied for the estimates. . . . Sediment Pick-up Threshold. The threshold dynamics can simply be thought of like this: while a particle lying on the seabed is subjected to the fluid forces of drag and lift, the weight of the particle and its position (frictional resistance) within the pack resist these forces. In currents, the pioneering experimental work was done by Shields (1936) – his graphical solution provides the threshold Shields Parameter as a function of particle Reynolds Number. As an attempt to make life easier for digital computation, Soulsby (1997) proposed an adaptation of this relation that helps one to estimate threshold depth-averaged velocity as a function of Particle Parameter. For waves, the estimation methods of the threshold are not very well-established. For the 0.5 mm seabed and the example wave, use of a relation proposed by Komar and Millar (1974) shows the peak threshold nearbed orbital velocity as 0.17 m/s. Comparatively, the exerted nearbed orbital velocities by the wave vary from the offshore -0.63 m/s to the onshore 1.2 m/s, passing through the zeros in-between. This indicates that there would be no motions of particles during some brief periods of the wave-cycle. . . . Suspension Criteria and Profile. The Suspension Number discussed earlier tells that particles remain in suspension when the bed-shear velocity is equal to or exceeds the particle settling velocity {also my paper: Discussion of ‘Simple Formula to Estimate Settling Velocity of Natural Sediments’ ASCE Jr of Waterway, Port, Coastal and Ocean Engg, 2004}. The same seabed sediment particle of 0.5 mm having a settling velocity of 6.1 cm/s (according to Rubey 1933), would require to have a fluid forcing bed-shear velocity larger than this. For the example wave, the equivalent peak bed-shear velocity is 7.9 cm/s yielding a Suspension Number of 1.3. The exercise indicates that the particles will remain suspended around the peak, but will tend to fall toward the bed during other phases of the wave-cycle. Once suspended, the nature of the suspension profile (a profile from a certain value at the surface to an exponentially increasing concentration near to the bed) will depend on the value of Rouse Number. The peak Rouse Number for the example wave, and the bed-material size is 1.92. Here again, one should note that this number varies over the wave cycle – which means that the fate of a suspended particle whether dropping on to the bed or remaining suspended, would depend on the particle’s position in the water column – the higher is its original position in the water column the lower is its chance of reaching the bed. The integration of the product of suspension and velocity profiles over the water depth (from a certain height above the bed) yields the suspended load transport. Such integrations are affected by some errors, however {my paper: Discussion of ‘Field Techniques for Suspended-sediment Measurement’, ASCE Journal of Hydraulic Engineering, 2001}. This happens because of the practical constraints of measurements in discrete intervals of space and time. . . . Sediment Transport Rate. Traditionally the derivations of sediment transport predictors are based on two approaches. The first is based on measurements that attempt to correlate the transport rate to some known hydraulic parameters. The second is based on laboratory experiments and scale-modeling tests relying on dimensional analysis of variables. These two approaches – often miss and obscure a very import aspect of sediment transport hydraulics – and it is the physics. Physics has the rare capability of enhancing one’s capability of understanding very complex problems. Help in this regard came from an unusual source – a World War veteran, Ralph Alger Bagnold (1896 – 1990). His ground breaking book, The Physics of Blown Sand and Desert Dunes (1941) proposed a relation of sand transport that depended on the fluid power. The fluid power is proportional to velocity, U raised to the power 3, U^3. It really makes sense because the forcing on the bed (bed-shear stress) to dislodge a particle is proportional to U^2. The transport flux or the power to transport the dislodged particles then becomes proportional to U^3. In a 42-page paper (US Geological Survey Professional Paper 422-I, 1966), An Approach to the Sediment Transport Problem From General Physics, Bagnold proposed the same approach to formulate the bed load and suspended load transports in steady water-current environments. His approach has been refined and reworked by many investigators – but the 1981 paper by JA Bailard, An Energetics Total Load Sediment Transport Model for Plane Sloping Beach made significant contributions – by adapting the Bagnold relation for oscillatory environments of waves. Among others, Bailard took the advantage of quadratic friction law to define the bed shear stress. His proposed relation popularly known as Bailard-Bagnold sediment transport formula is gaining popularity in recent times. The formula reflects bed load transport as proportional to U^3, and the suspended load transport requiring more energy to overcome the settling velocity as proportional to U^4. In this piece, I will demonstrate the application of this relation for the example wave, to show the cross-shore sediment transport outside the surf zone where wave asymmetry or nonlinearity plays a significant role. To illustrate the application of this method – I have included an image showing the wave surface of the example 2-meter high 12-second wave, and instantaneous cross-shore bed, suspended and total load transports for 2-wave cycles. It is assumed that the wave approaches the shore directly with its crest parallel to the shore. At 10-meter water depth on a seabed slope of 1/50 and a median sand particle diameter of 0.5 mm, the wave becomes asymmetric or nonlinear (Ursell Number U = 26.8) indicating the heightening of the crest and flattening of the trough. As expected, the image shows high onshore transports under the crest (maximum onshore nearbed orbital velocity 1.19 m/s) and low offshore under the trough (maximum offshore nearbed orbital velocity -0.63 m/s). In terms of the total load transport per meter parallel to the shore – the maximum onshore is 0.71 kg/s, and the maximum offshore is -0.07 kg/s – with the net onshore transport during one wave cycle as 2.13 kg. The ratios of suspended load to bed load vary from 0.01 to 2.4. If the period of the 2-meter wave is reduced to 5-second (the wave steepness increases to 0.06), linear wave theory applies (U = 2.7), and the net onshore transport reduces to 0.12 kg per meter parallel to the shore. The period-effect of nonlinearity and high net onshore transport is one simple example of beach build-up that happens in most beaches during the summer-time season of low-steepness swells. Like many other sediment transport predictors, Bailard-Bagnold formula is not without limitations. To allow some flexibility in this regard, the formula allows it to calibrate to measurements by two adjustments – the bed-load and the suspended load efficiency factors. Like the colossal amount of literature in sediment dynamics, this piece turned out to be another long piece in the WIDECANVAS. Well, I suppose one needs to make things clear one is attempting to explain. Let me finish this piece with a quote from Albert Einstein (1879 – 1955), who reportedly asked his son Hans Einstein, Why is it that you wish to study something so complicated? Hans Einstein indeed saw the complicated sediment transport problem more profoundly – in terms of probability theory – proposing his own probabilistic sediment transport formula (Einstein 1950). . . . . . - by Dr. Dilip K. Barua, 15 November 2017
0 Comments
Leave a Reply. |

 RSS Feed
RSS Feed
