The Surf Zone

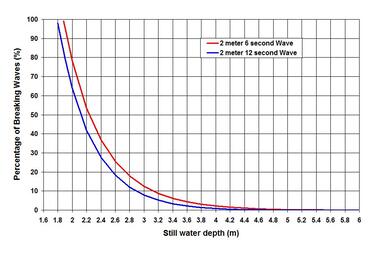We have talked about the Natural waves in four blogs – Ocean Waves, Linear Waves, Nonlinear Waves and Spectral Waves on the NATURE page, and in the Transformation of Waves piece on the SCIENCE & TECHNOLOGY page. In this piece let us turn our attention to the most dynamic and perhaps the least understood region of wave processes – the surf zone – the zone where waves dump their energies giving births to something else.

1. The Surf Zone
What is the surf zone? The Surf zone is the shoreline region from the seaward limit of initial wave breaking to the shoreward limit of still water level. The extent of this zone shifts continuously – to shoreward during high tide and to seaward during low tide – to shoreward during low waves and to seaward during high waves. The wave breaking leading to the transformation – from the near oscillatory wave motion to the near translatory wave bores – is the fundamental process in this zone. Note that by the time a deep-water spectral wave arrives at the seaward limit of the surf zone, its parent spectrum has already evolved to something different, and the individual waves have become mostly asymmetric or nonlinear. 
In the process of breaking a wave dumps its energy giving birth to several responses – from the reformation of broken waves, wave setup and runup, and infragravity waves – to the longshore, cross-shore and rip currents – to the sediment transports and morphological changes of alluvial shores. The occurrence, non-occurrence or extents of these responses depends on many factors. It is impossible to treat all these processes in this short piece. Therefore I intend to focus on some fundamentals of the surf zone processes - the processes of wave breaking and energy dissipation.
.  .  .
2. Characterizing the Processes
How are the surf zone processes treated in mathematical terms? Two different methods are usually applied to treat the problem. The first is based on the approximation of the Navier-Stokes (French engineer Claude-Louis Navier, 1785 – 1836; and British mathematician George Gabriel Stokes, 1819 – 1903) equation. In one application, it is based on the assumption that the convective acceleration is balanced by the in-body pressure gradient force, wave forcing and lateral mixing, and by surface wind forcing and bottom frictional dissipation.
The second approach is based on balancing two lump terms – the incoming wave energy and the dissipated energy. We have seen in the Linear Waves piece on the NATURE page that wave energy density is proportional to the wave height squared. In a similar fashion, the dissipated wave energy is proportional to the breaking wave height squared multiplied by some coefficients. Both the approaches are highly dependent on the empirical descriptions of these coefficients – making the mathematical treatment of the problem rather weak.
.  .  .
2.1 Energy Dissipation
Let us focus on the energy approach – how the breaking energy dissipation occurs in the surf zone. Many investigators were involved in formulating this phenomenon. For individual monochromatic waves, the two most well-knowns are: the one proposed by M.J.F. Stive in 1984 and the other one proposed by W.R. Dally, R.G. Dean and R.A. Dalrymple in 1985.
It was the energy dissipation formulation by J.A. Battjes and J.P.F.M. Janssen in 1978 that addressed the energy dissipation processes of spectral waves. This formulation required an iterative process, and was therefore cumbersome to apply. However with the modern computing power, that hurdle does not exist any more. In addition to the aforementioned investigators, there are many others who modified and refined the formulations and understandings of the surf zone processes.
In this piece let us attempt to see how the energy dissipation works for spectral waves. Among the coefficients influencing the energy dissipation is a factor that defines how fractions of the spectral wave group break. This factor is very important, and let my try to illustrate how that works – by solving the term iteratively.      
.  .  .          
2.2 Wave Breaking - the Surf Similarity Number
Before doing that let me highlight some other understandings of the surf zone processes. Early investigators of the surf zone processes have noticed some important wave breaking behaviors – that all waves do not break in the same fashion and on all different beach types. Their findings led them to define an important dimensionless parameter – the Surf Similarity Number (SSN) – also known as the Iribarren Number (after the Spanish engineer Ramon Cavanillas Iribarren, 1900 – 1967; C.R. Iribarren and C. Nogales, 1949) – or simply the Wave Breaking Number. This number is the product of beach slope and wave steepness – and is directly proportional to the beach slope and inversely proportional to the square root of wave steepness (steepness is the ratio of wave height and wave length – long-period swells are less steep than short-period seas). Either of these two parameters could define a breaker type.     
To identify the different breaker types it is necessary to define some threshold SSN values. Among the firsts to define the threshold values were C.J. Galvin (1968) and J.A. Battjes (1974), but more lights were shed by many other investigators later. On the lower side, when the SSN is less than 0.5, the type is termed as Spilling Breaker – it typically occurs on gently sloping shores during breaking of high-steepness waves – and is characterized by breaking waves cascading down shoreward creating foamy water surface. On the upper side, when the SSN is higher than 3.3, the type changes to Surging and Collapsing Breakers. In a surging breaker, waves remain poorly broken while surging up the shore. In a collapsing breaker, the shoreward water surface collapses on the unstable and breaking wave crest. Both of these breakers typically occur in steep shores during periods of incoming low-steepness waves.  
When the SSN ranges between 0.5 and 3.3, the type becomes a Plunging Breaker – it typically occurs on intermediate shore types and wave steepness – and is characterized by curling of shoreward wave crest plunging and splashing on to the wave base. This type of breaker causes high turbulence, and sediment resuspension and transport on alluvial shores. An example of sediment transport processes and associated uncertainties in the surfzone is in the Longshort Sand Transport.
.  .  .
2.3 Quantifying the Breaking Waves
Perhaps it is helpful if we think more for a while, of what happens in the surf zone – as one watches the incoming waves – high and low – breaking at different depths propagating on to the shore. What prompts wave breaking? The shallow water wave-to-wave interaction – Triad lets wave spectrum evolve into a narrow band shifting the peak energy to high frequencies. The concentration of wave energies lets a wave-form to become highly nonlinear and unsustainable as the water particle velocity exceeds the celerity (square root of the product of acceleration due to gravity and depth), and right before breaking it takes the shape of a solitary wave (a wave that does not have a definable trough). I have tried to throw some lights on this breaking process in my short article published in the 2008 ASCE Journal of Waterway, Port, Coastal and Ocean Engineering {Discussion of ‘Maximum Fluid Forces in the Tsunami Runup Zone’}.
Further, we have discussed in the Transformation of Waves piece on this page that a wave cannot sustain itself when it reaches the steepness at the threshold value of 1/7 and higher. A criterion proposed by Miche [Le pouvoir reflechissant des ouvrages maritimes exposes a l’action de la houle. 1951] captures the wave breaking thresholds not only due to the limiting steepness, but also due to the limiting water depths in shoaling water. In 1891, J. McCowan has shown that wave breaks when its height reaches 4/5th of the water depth on flat bottom.
Now that we know the wave breaking types and initiation, let us try to understand how the energies brought in by the waves are dissipated. To illustrate the process I have included an image showing the percentage of fractional energy dissipation, as two spectral waves – a 2-meter 6-second and a 2-meter 12-second – propagate on to the shore.                       
As demonstrated in the image, spectral waves begin to lose energy long before the final breaking episode happens. This means that the transformation process lets the maximums of the propagating spectrum to break as they reach the breaking threshold. In addition, as expected the shorter period waves (see the 6-second red line) lose more energy on way to the shallow water than the longer period (see the 12-second blue line) ones. 
By the final breaking, all the energies are dissipated giving births to other processes (water level change, nearshore currents and sediment transport). On a 1 to 10 nearshore slope, the SSN for the two cases are 0.5 and 1.1, respectively – indicating a Plunging Breaker type – but at two different scales. On most typical sandy shores, the long period waves are more likely to end up being a Plunging Breaker than the short-period ones. At the final stage, the breaking wave heights are 76% and 79% of water depths for the two cases.
.  .  .
Does anyone see another very important conclusion from this exercise? Well this conclusion is that, for any given depth and wave height the long-period waves bring in more energy to the shore than the shorter ones – the period effect. Let us attempt to see more of it at some other time. 
Some more insights on the surf zone waves are provided by Goda (Yoshima Goda, 1935 – 2012) describing a graphical method to help determine wave height evolution in the surf zone. His graphs show, for different wave steepness and nearshore slopes, how the maximum and the significant wave heights evolve on way from the deep water to the final breaking – and then to the reformed waves after final breaking. 

.  .  .  .  .

- by Dr. Dilip K. Barua, 10 November 2016 

---