Science and technology
working with nature- civil and hydraulic engineering to aspects of real world problems in water and at the waterfront - within coastal environments
 In the Common Sense Hydraulics blog on this page, I have pointed out that the first order solution to a hydrodynamic problem is governed by the actives forces of excess water pressure and gravitational pull resisted by the reactive friction force. It only makes sense that I devote this piece as a follow up on the reactive friction force. This force is caused by the resistance of a solid boundary to the fluid flow of mass and energy on it. Reactive forces are notoriously nonlinear, not only because of the fluid behavior itself, but also because of the mobility of the bed if it happens to be alluvial. Why understanding resistance to flow is important? One reason is that the first order solution, either in desktop analysis or in computational modeling cannot be achieved unless the reactive resistance is accurately understood and parameterized. In addition, without an accurate first order solution that dominates processes, advanced order solutions are unachievable. The second reason is that the stability and functions of a shoreline, and waterfront and maritime structures can be jeopardized if the understanding of erosion-sedimentation processes remains questionable. . . . Before entering into the discussion of the topic, I am tempted to add a few lines on the history of coastal engineering. The official recognition and definition of it was launched at the First Conference on Coastal Engineering held in Long Beach, California in 1950. The conference proceedings contributed by some invited speakers gave birth to this new discipline of civil hydraulic engineering. In time, the discipline metamorphosed into several sub disciplines – not so much in an orderly fashion but rather in a confusing manner. Apart from journal papers and conference proceedings, the initiative was followed by some remarkable books. Among them were three outstanding ones. The first was a volume {Estuary and Coastal Hydrodynamics. McGraw-Hill, 1966} edited by Arthur T. Ippen (1907 – 1974). The second was an initiative taken by the American Society of Civil Engineers (ASCE) that resulted in a volume {Sedimentation Engineering. ASCE, 1974} edited by Vito A. Vanoni (1904 – 1999). Contributed by outstanding scholars from around world, these two publications set the scientific background on which many future works were built upon. Another publication {Shore Protection Manual (SPM), Vol. I and II} dealing with the guidelines on practical applications was initiated by U. S. Army Coastal Engineering Research Center (CERC). First published in 1973, these two SPM volumes soon became very popular with practicing engineers, and CERC continued issuing new editions, the last of which was in 1984. In later years, SPM reincarnated into the diverse and multiple Coastal Engineering Manuals (CEM). During and following the publications of these three volumes, universities and research institutions of many different countries made significant contributions: notable among them were Delft Hydraulics, HR Wallingford, and Japan. An edited book, {History and Heritage of Coastal Engineering} by Nick Kraus published in 1996 chronicled the development of the discipline. . . . Well, enough on the historical context for now. Let us try to focus on the topic of this piece. But before doing so, a very important concept requires clarification - and this concept is regarding the boundary layer. This layer of reduced flow velocity develops closed to the bed – from zero near the bed to the asymptote of free stream velocity up in the water column. The reduced velocity is mainly caused by the shearing resistance of the bed, and the loss of fluid flow energy in eroding and transporting alluvial sediments. The layer divided primarily into two is known as the boundary layer. A very thin viscous sub-layer occurs near the bed with a turbulent upper layer above. Interactions between the fluid shearing force and the bottom reactive force within this layer account for viscous and turbulent transfer of momentums within the water column. Described by an asymptotic logarithmic or a power function, the height of this layer changes in response to the change in flow velocities and roughness of the bed. Among other investigators, my own works {Some Aspects of Turbulent Flow Structure in Large Alluvial Rivers. Journal of Hydraulic Research, Taylor & Francis, 1998} for the Flood Action Plan – River Survey Project, provide some insights into the flow structure of the boundary layer. The investigation showed that the bed-generated turbulence in the presence of high dune-scale bedforms reached the maximum above the bed at a height of 5 to 10% of water depth, with decaying of the strength from above that level to up in the water column. A bedform is a wavy undulation, mostly noticeable in a sandy bed, which is primarily asymmetric in unidirectional flows and symmetric in oscillatory short-wave environments. The image shown in this piece gives a snapshot of some small-scale bedforms. . . . How to characterize the bed resistance? The question can best be answered using the theory proposed by Daniel Bernoulli (1700 – 1782). His formulation shows that dynamic water pressure or kinetic energy is defined in terms of V^2, V being the mean flow velocity of the current. It is this dynamic pressure that is responsible for exerting drag on the bed. We will find out in later discussions that it is also this dynamic pressure that causes drag force on structures in water. Many, including one of the pioneering investigators Ralph Alger Bagnold (1896 – 1990) used this drag to formulate the bed shear force or the equivalent bottom reactive force and sediment transport. The formulation known as quadratic friction law defines this force as the product of a non-dimensional drag coefficient, water density and square of the current velocity. The quadratic friction law is universally applicable in unidirectional flow such as in river as well as in oscillatory long-wave motions such as tide, tsunami or storm surge. The drag coefficient is related to its counterparts of other known resistance coefficients such as Chezy (Antoine Chezy, 1718 – 1798) coefficient C, Manning’s (Robert Manning, 1816 – 1897) n, and Darcy-Weisbach friction factor f. To give an idea, it can be shown that in a water depth of 10 m, and a representative bed-material size of 3 mm, the drag coefficient is 0.0014, C = 84.13 m^(1/2)/s, n = 0.0175 (s/m^(1/3)) and f = 0.0111. See more in Seabed Roughness of Coastal Waters. When deformation of the alluvial bed occurs in high flow stages, additional resistance to flow is imposed. The migrating bedforms varying from ripples to large dunes are mostly asymmetric with a flatter stoss slope and steeper avalanche slope. In most instances, the larger the bedform, the larger is the resistance to flow. In one investigation {Bedform Dynamics and Sediment Transport – Report of an Investigation in the Jamuna River. Institution of Engineers Bangladesh, Paper #41-4-06, 1996} I worked on; it was found that bedforms accounted for 70% of the total bed resistance. . . . The bed resistance discussed so far is applicable for unidirectional flow, and for tide, tsunami and storm surge. How about the bed resistance to short-wave oscillatory motions? The quadratic friction law is similarly applicable in short-wave motions with the applicable velocity taken as the amplitude of bottom orbital velocity; and the drag coefficient is renamed as a wave friction factor. The wave orbital velocity is a bidirectional vector with a peak on either direction. This peak is the amplitude. In addition, a relation proposed by Swart {Offshore sediment transport and equilibrium beach profiles. Delft Hydraulics Publication No. 131, 1974} shows that the amplitude of the bottom orbital excursion affects the wave friction factor. As an example, at a water depth of 10 m, and a representative bed-material size of 3 mm, the friction factor is 0.0175 for a 2-meter 10-second wave. Similar to unidirectional flow, presence of bedforms which are mostly symmetric in short-wave environments, the frictional resistance is enhanced. In a hydraulic environment where both long and short waves are active, the wave-current friction factor accounts for both. The resistances triggered by both the sources are added in some fashion that depends on the relative magnitudes of current and the amplitude of bottom wave orbital velocity. Well, I am not sure whether I have managed to explain the topic in plain English as promised. I have tried to keep things as simple as possible with only some limited but unavoidable use of scientific jargon. One more thing. It is important to mention that the materials covered in this piece are highly empirical, which means that there is no single value of coefficients applicable for all different cases, and for all hydraulic environments. Empirical coefficients are usually valid in orders of magnitudes, and they require verification to examine their applicability for specific cases. If that is not possible their limitations and uncertainties should be highlighted. . . . Here is an anecdote to ponder: The disciple asked the master, “Sir, how would you see the resistance to flow in a wider social context?” The master smiled, “Well, the cause-effect, force-response or action-reaction duo is universally present everywhere. Things are even more complicated in a society than the complexities of fluid flow. What we are talking about here are positive actions or endeavors, and reactions of them. We used to hear from elders in our childhood that life was full of thorns. So resistances are there no matter how we don’t want them.” “Could you elaborate please?” “In a society, resistance could come from individuals or from a collective bunch. But while a reactive resistance in natural fluid flows is instantaneous, the same in social interactions could be instantaneous, delayed or even absent. If delayed, the reactive resistance can metamorphose into something different and subdued. Therefore it is often helpful to delay high emotional reactions. But in a society not all resistances are reactive. Some are active resistances which could either mean something good, or could mean something malicious. Some malicious resistances could even reach the scale of an obstacle.” “Thank you Sir. When do you think active social resistances can become damaging.” “Well, the effects could become very frustrating, ugly and damaging when a society promotes, or is founded upon division, mistrust and conflict.” . . . . . - by Dr. Dilip K. Barua, 11 August 2016
0 Comments
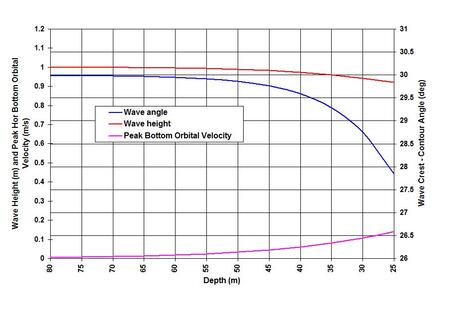 We have tried to see Ocean Waves in the NATURE page through the eyes of a scientist and a poet. In this piece let us try to see how the born waves are transformed as it propagates – this time through the eyes of an applied scientist or engineer. I will mainly focus on ocean waves, although the discussed transformation processes apply to all different types of waves. A natural water wave is the undulated response of water to transport the energy it gains – through the attractions of Sun and Moon as in a tide, sudden massive ocean floor rupture as in a tsunami, hurricane storms piling huge water mass as in a storm surge and, of course, through the blowing winds causing ubiquitous ocean wind-waves. The born waves are visible in the duality of crests and troughs, but are composed of multiple waves of different periods and heights built within them (as are vivid in harmonic decomposition of tidal waves, as well demonstrated in my 1991 COPEDEC-PIANC paper: Tidal observations and spectral analyses of water level data in the mouth of the Ganges-Brahmaputra-Meghna river system). Natural waves are spectromatic not only in terms of periods, heights and phases but also in directions. Some basics of wind-wave hindcasting and forecasting methods are reviewed in one of my publications {Wave Hindcasting. Encyclopedia of Coastal Science, Springer, 2005. Updated 2017}. As soon as a wave is born, it is subjected to the transformation processes as the energy propagates. The processes can best be described by three important parameters: wave height H, the height from trough to crest; local wave length L or wave period T, measured simply from crest to crest; and the local still water depth d. A very useful parameter proposed by Fritz Joseph Ursell (1923 – 2012) does use these three parameters to classify waves - to indicate whether they can be approximated by the 1st order processes of Linear Wave Theory proposed by George Biddell Airy (1801 – 1892). This parameter named in his honor as Ursell Number describes a threshold combining the two ratios H/d and d/L, and is given by U = HL^2/d^3. It turns out that for all practical purposes, waves can be assumed to be symmetric or linear, when U is equal to or less than 5.0. Further, it is important to know that a wave cannot sustain itself when it reaches the steepness at the threshold value of 1/7 or higher – steepness being the ratio of H over L. The unsustainability results in wave breaking and losses of energy – which is mostly seen as whitecaps in noisy wind waves. A criterion proposed by Miche {Le pou voir reflechissant des ouvrages maritimes exposes a l’action de la houle. 1951} captures the wave breaking thresholds not only due to the limiting steepness, but also due to the limiting water depth. . . . Next, it is useful to delineate the wave transformation region for convenience. A deep-water zone covers the areas where depths are higher than half of the wave length, L/2. The contiguous shallower region is known as the refraction zone and it starts from the deep-water limiting depth to the region where wave breaks, roughly at d = 1.28H in flat bottom. In reality, wave spectrum and beach slope also play a role in controlling depth-limited wave breaking. In the refraction zone waves start to feel the bottom and several changes happen in this zone – in particular the symmetry of the sinusoidal deep-water wave is lost by distortion – turning it into asymmetric at U = 5.0 or higher. In this piece we will be mostly talking about these two zones, but only the symmetric aspect of it. The nonlinear asymmetric wave phenomenon is highly elaborate by its own right, and hope that I will visit it at some other time. After breaking, the transformation processes result in dissipation of the entire wave energy in the surf zone, and to up in the beach slope in the swash zone. The dissipated wave energy rushes up the shore as a bore of very high velocity. As the energy is dissipated, water rushes down the slope by gravitational pull and by the suction of trough. Vigorous turbulence and sand movement characterize this zone shaping and reshaping the shoreline morphology. Again, it is helpful to focus on these processes separately and I hope to come back to it at a later time. . . . With these understandings let us turn our attention to see how waves are transformed. The dynamic equilibrium of things requires that the characteristics of transformed waves are determined by the balance of incoming energy against those due to dissipation, transmission and reflection. To keep this discussion to a manageable level, I will try to focus on wind waves. Waves developed by wind storms are highly irregular, noisy and short-crested, and the energy dissipation starts immediately by the interactions between the born waves and the lashing wind prompting steepness related breaking. . . . Among others, three other notable processes also start immediately in deep-water wave motions. The first is known as the frequency dispersion – frequency is the reciprocal of period, which means that a wave with a period of 10 second has a frequency of 0.1 hertz. This process involves separation of the long period components as they start to travel faster leaving behind the short-period ones. This is the reason why we see the fore-runners – long-period long-crested swells on coasts that have traveled far away from their sources of origin at a storm field. The second is the spectral evolution of waves through the wave to wave interactions. In a spectrographic display, peak wave energy proportional to H^2, is seen as concentrated at a certain frequency. The evolution process accounts for spreading out this energy in both ways toward the higher and lower frequencies, and also in directions. Those transferred to the higher frequency domain mostly break as the limiting steepness is reached, and can be seen as whitecaps. The third is the grouping of waves seen in the togetherness of high ones separate from the low ones. As pointed out in the Ocean Waves blog in the NATURE page, this process appears to result from the superimposition of component waves of different heights, periods and phases. The grouping, in essence imposes an additional long period wave envelope. . . . What are the simplest things that happen in the refraction zone? Let us list some of the simple processes in this zone. With the decreasing water depth toward the shore, the wave speed or the celerity of the wave energy slows down, the wave length decreases, but the wave orbital velocity increases. To demonstrate the processes, I have constructed a simple image shown in this piece. In this image, a 1-meter, 8-second wave approaching the shore-parallel contour at a 30-degree angle is followed on its journey to transformation. The shown analysis is limited within a region where the wave processes can be approximated by the Linear Wave Theory at U = 5.0. As the waves begin to lose its properties of symmetry shoreward, the processes start to become complicated, and I hope to come back to that at some other time. But I like to touch upon one simple aspect of non-linearity known as the Stokes Drift. . . . Stokes Drift named after the British mathematician George Gabriel Stokes (1819 – 1903) represents a residual current, also known as the mass transport velocity heading in the direction of wave propagation. The residual current is about 1-order less than the peak orbital velocity – which means that for a peak orbital velocity of 1 meter per second, the Stokes Drift would be about 0.1 meter per second. This non-linear effect was shown by Stokes by solving the unsteady Bernoulli (1700 – 1782) equation to the 2nd order. Stokes Drift explains the reasons why objects floating in the ocean finally end up on the shore, even in the absence of an appreciable ocean current. Apart from the nonlinear transformation, at least four other processes happen contributing to the evolution of waves in the refraction zone. These are reshuffling of wave energy, wave bending or refraction that accounts for wave crests becoming parallel to the shore, shoaling of waves, and frictional dissipation of wave energy at the bottom. It turns out that the frictional dissipation is very negligible in the linear wave region. While spreading out of the peak energy occurs in deep-water, in the shallow refraction zone the wave to wave interactions results in a one way process – the transfer of the peak energy to the high frequencies. The process results in a spectral evolution that approaches the specter of a solitary monochromatic wave. This is one of the reasons why the ratio of group celerity to individual wave celerity increases from n = 0.5 in deep-water to n = 1.0 in very shallow water. . . . Let us now turn our attention to the processes of refraction and shoaling. The attached image shows how the wave approaching at an oblique angle of 30 degrees is reduced to less than 28 degrees. This refraction process occurs due to the slowing down of wave celerity as it crosses the boundary from relatively deep water to a shallower area. It has been formulated by Dutch Astronomer Willebrord Snellius (1580 – 1626) for optics, and the refraction process is known as the Snell’s Law. As obvious in optics, refraction causes a brilliant light to become softer – so does a water wave – becoming less energetic by losing some of its energy in the process. While the refraction process causes the waves to lose energy, another process known as shoaling causes the waves to amplify. This process can simply be explained by the fact that as the wave length decreases, and the celerity slows down, the height has to increase to balance the energy. The contrasting influences of the refraction and shoaling processes results in a transformation that indicates the initial loss of energy density or lessening of wave height if the wave approach angle is high, and heightening of waves further shoreward. While this happens, the peak bottom orbital velocity gains strength as both the depth and wave length continue to decrease. What is the implication of reducing wave celerity and increasing orbital velocity? With waves becoming nonlinear, depth-limited wave breaking is initiated when a wave form can no longer be sustained because the increasing orbital velocity overtakes the decreasing celerity at some point. In a short article I have demonstrated how that happens in the case of an uprushing tsunami {Discussion of Maximum Fluid Forces in the Tsunami Runup Zone. ASCE Journal of Waterway, Port, Coastal and Ocean Engineering, 2008}. . . . Here is an anecdote to ponder: The disciple asked the master, “Sir, how am I today from yesterday?” The master smiled, “My friend that is a difficult question. But note this, as long as life’s energy flows, the response in humans occurs through the rise and fall of emotions and thought processes, like the crest and trough of a wave. And while all that happens, a human is transformed from one state to another. So the past you may not be the same you today, although your physical body is same like the water on which wave propagates. This is just how the dynamics of life, society and Nature work.” “Could I have been worse or better than yesterday?” “It all depends. Like the gravity tries to restore the wave undulations, so does the foundation in all of us. If you are built upon strong humane values, chances are that you are heading toward improving yourself. But a single day is too short a time to show any change in life.” . . . . . - by Dr. Dilip K. Barua, 4 August 2016 |