Science and technology
working with nature- civil and hydraulic engineering to aspects of real world problems in water and at the waterfront - within coastal environments
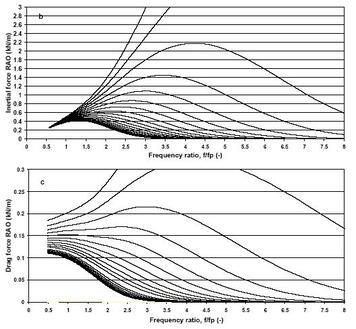 Most of the materials in this piece are based on my 2008 ISOPE (International Society of Offshore and Polar Engineers) paper: Wave Loads on Piles – Spectral Versus Monochromatic Approach. This paper discusses, for both monochromatic and spectral waves, how the Morison forces (Morison and others, 1950) compare for a surface piercing round vertical pile in some cases of waves with Ursell Numbers (Fritz Joseph Ursell, 1923 – 2012), U in the order of 5.0. I have included an image (courtesy ISOPE) from this paper showing inertial and drag force RAOs as a function of frequency. The RAO or Response Amplitude Operator represents the maximum force for a unit wave height. . . . Standing in the nearshore water of unbroken waves, one experiences a shoreward push when a wave crest passes and a seaward pull when a wave trough passes – and if the waves happen to be large he or she may experience dislodging from the foothold. The immediate instinct is to recognize the power of a wave in exerting forces on members standing on its way – resisting its motion. How to estimate these forces? Do structures of all different sizes experience the same type of forces? The answer to the first question depends on how well one answers the second question – how the structure sizes up with the wave – the wave length (L) to be exact. It turns out that the nature of wave forces on a structure can be distinguished based on the value of a parameter known as the diffraction parameter – a ratio of the structure dimension (D) perpendicular to the direction of wave advance, and the local wave length, L. When D is less than about 1/5th of L, the structure can be treated as slender and wave forces can be determined by the Morison equation. . . . In this piece let us attempt to see how the Morison forces work – how the forces apply in considerations of both monochromatic and spectral waves. I will also touch upon the nonlinear wave forces. Slender structures exist in many port and offshore installations as vertical structures – as mono pile and pile-supported wharfs in ports – as gravity platforms and jacket structures in offshore structures – and as horizontal structural members and pipelines. What are the Morison forces? They are the forces caused by the wave water particle kinematics – the velocity and acceleration. The two kinematics causing in-line drag and inertial horizontal forces are hyperbolically distributed over the height of a vertical standing structure – decreasing from the surface to the bottom. For a horizontal pipeline, the loads include both the in-line horizontal forces as well as the hydrodynamic vertical lift force. More about these to-and-fro wave forces? The drag force is due to the difference in the velocity heads between the stoss and lee sides of the structure; and the inertial force is due to its resistance to water particle acceleration. The hydrodynamic lift force is due to the difference in flow velocities between the top and bottom of a horizontal structure. I will attempt to talk more about it at some other time. Do the slender members change the forcing wave character? Well while the structures provide the resistances by taking the forces upon themselves; they are not able to change the character of the wave – because they are too small to do so. From the perspectives of structural configuration, when a vertical member is anchored to the ground but free at the top, it behaves like a cantilever beam subjected to the hyperbolically distributed oscillating horizontal load. When rigid at both ends, the member acts like a fixed beam. For a horizontal pipeline supported by ballasts or other rigidities at certain intervals, it also acts like a fixed beam with the equally distributed horizontal drag and inertial forces and the vertical hydrodynamic lift forces. . . . Before entering into the complications of spectral and nonlinear waves, let us first attempt to clarify our understanding of how linear wave forces work. We have seen in the Linear Waves piece on the NATURE page that the wave water particle orbital velocity is proportional to the wave height H, but inversely proportional to the wave period T. The water particle acceleration is similarly proportional to H, but inversely proportional to T^2. The nature of proportionality immediately tells us that waves of low steepness (H/L) have lower orbital velocities and accelerations – therefore they are able to cause less forces than the waves of high steepness. For symmetric or linear waves, the orbital velocity and acceleration are out of phase by 90 degrees. In the light of Bernoulli Theorem (Daniel Bernoulli, 1700 – 1782) dealing with the dynamic pressure and velocity head, the drag force is proportional to the velocity squared. Both the drag and inertial forces must be multiplied by some coefficients to account for the structural shape and for viscosity of water motion at and around the object. Many investigators devoted their times to find the appropriate values of drag and inertia coefficients. A book authored by T. Sarpkaya and M. Isaacson published in 1981 has summarized many different aspects of these coefficients. Among others the coefficients depend on the value of Reynolds Number (Osborne Reynolds, 1842 – 1912) – a ratio of the product of orbital velocity and structure dimension to the kinematic viscosity. The dependence of the forces on the Reynolds Number suggests that a thin viscous sublayer develops around the structure – and for this reason the Morison forces are also termed as viscous forces. The higher the value of the Reynolds Number, the lower are the values of the coefficients. The highest drag and inertial coefficients are in the range of 1.2 and 2.5, respectively, but drag coefficients as high as 2.0 have been suggested for tsunami forces. . . . How do the drag and inertial forces compare to each other? Two different dimensionless parameters answer the question. The first is known as Keulegan-Carpenter (G.H. Keulegan and L.H. Carpenter, 1958) Number KC; it is directly proportional to the product of wave orbital velocity and period and inversely proportional to the structure dimension. It turns out that when KC > 25 – drag force dominates, and when KC < 5 inertia force dominates. The other factor is known as the Iversen Modulus (H.W. Iversen and R. Balent, 1951) IM, is a ratio of the maximums of inertia and drag forces. It can be shown that both of these two parameters are related to each other in terms of the force coefficients. While the horizontal Morison force is meant to result from the phase addition of the drag and inertial forces, which are 90 degrees out of phase, the conventional engineering practice ignores this scientific fact, instead adds the maximums of the two together. This practice adds a hidden factor of safety (HFS) in design forces. For example, a 2-meter, 12-second wave acting on a 1-meter vertical structure standing at 20-meter of depth (U = 6.4) would afford a HFS of 1.45. However HFS varies considerably with the changing values of IM – with the highest occurring at IM = 1.0, but decreases to unity at very high and low values of IM. How does the wave nonlinearity affect the Morison forces? We have seen in the Nonlinear Waves piece on the NATURE page that the phase difference between the velocity and acceleration shifts away from 90 degree – with the increasing crest water particle velocity and acceleration. For the sake of simplicity, let us focus on a 1-meter high 8-second wave, propagating from the region of symmetry at 10 meter water depth (U = 5.0) to the region of asymmetry at 5 meter water depth (U = 22.6). By defining and developing a relationship between velocity and acceleration with U, it can be shown the maximum linear and nonlinear forces are nearly equal to each other at U = 5.0. But as the wave enters into the region of U = 22.6, the nonlinear drag force becomes 36% higher than the linear drag force. The nonlinear inertia force becomes 8% higher than the linear one. With waves becoming more nonlinear in shallower water, the percentage increases manifold higher than the ones estimated by the linear method. While the discussed method provides some insights on the behaviors of nonlinear Morison forces, USACE (US Army Corps of Engineers) CEM (Coastal Engineering Manual) and SPM (Shore Protection Manual) have developed graphical methods to help estimating the nonlinear forces. . . . Now let us turn our attention to the most difficult part of the problem. What happens to the Morison forces in spectral waves? How do they compare with the monochromatic forces? To answer the questions, I will depend on my ISOPE paper. The presented images from this paper shows the inertial and drag force RAOs over the 20-meter water depth at 1-meter interval from the surface to the bottom – for a 2-meter high 12-second wave acting on a 1-meter diameter round surface-piercing vertical pile. The forcing spectral wave is characterized by JONSWAP (Joint North Sea Wave Project) spectrum (see Wave Hindcasting). For this case, the RAOs are the highest at frequencies about 3.5 times higher than the peak frequency (fp) of 0.08 Hertz (or 12-second). This is interesting because the finding is contrary to the general intuition that wave forces are high at the frequency of the peak energy – the period effects on wave kinematics! As the frequency decreases, the inertial force RAO diminishes tending to zero. The drag force RAO, on the other hand, tends to reach a constant magnitude as the frequency decreases. This finding confirms that at low frequency motions of tide and tsunami, the dominating force is the drag force (which is also true for cases when KC > 25.0). How do the spectral wave forces compare with the monochromatic wave forces? It turns out that for the case considered, the monochromatic method underestimates the wave forces by about 9%. A low difference of this order of magnitude is good news because one can avoid the rigors of the spectral method to overcome such a small difference – the difference of this magnitude is in the range of typical uncertainties of many parameters. . . . . . - by Dr. Dilip K. Barua, 17 November 2016
0 Comments
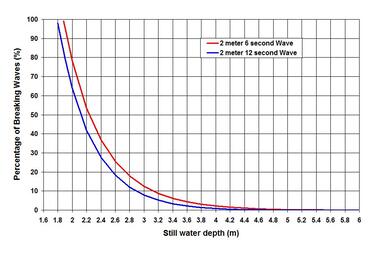 We have talked about the Natural waves in four blogs – Ocean Waves, Linear Waves, Nonlinear Waves and Spectral Waves on the NATURE page, and in the Transformation of Waves piece on the SCIENCE & TECHNOLOGY page. In this piece let us turn our attention to the most dynamic and perhaps the least understood region of wave processes – the surf zone – the zone where waves dump their energies giving births to something else. What is the surf zone? The Surf zone is the shoreline region from the seaward limit of initial wave breaking to the shoreward limit of still water level. The extent of this zone shifts continuously – to shoreward during high tide and to seaward during low tide – to shoreward during low waves and to seaward during high waves. The wave breaking leading to the transformation – from the near oscillatory wave motion to the near translatory wave bores – is the fundamental process in this zone. Note that by the time a deep-water spectral wave arrives at the seaward limit of the surf zone, its parent spectrum has already evolved to something different, and the individual waves have become mostly asymmetric or nonlinear. In the process of breaking a wave dumps its energy giving birth to several responses – from the reformation of broken waves, wave setup and runup, and infragravity waves – to the longshore, cross-shore and rip currents – to the sediment transports and morphological changes of alluvial shores. The occurrence, non-occurrence or extents of these responses depends on many factors. It is impossible to treat all these processes in this short piece. Therefore I intend to focus on some fundamentals of the surf zone processes - the processes of wave breaking and energy dissipation. . . . How are the surf zone processes treated in mathematical terms? Two different methods are usually applied to treat the problem. The first is based on the approximation of the Navier-Stokes (French engineer Claude-Louis Navier, 1785 – 1836; and British mathematician George Gabriel Stokes, 1819 – 1903) equation. In one application, it is based on the assumption that the convective acceleration is balanced by the in-body pressure gradient force, wave forcing and lateral mixing, and by surface wind forcing and bottom frictional dissipation. The second approach is based on balancing two lump terms – the incoming wave energy and the dissipated energy. We have seen in the Linear Waves piece on the NATURE page that wave energy density is proportional to the wave height squared. In a similar fashion, the dissipated wave energy is proportional to the breaking wave height squared multiplied by some coefficients. Both the approaches are highly dependent on the empirical descriptions of these coefficients – making the mathematical treatment of the problem rather weak. . . . Let us focus on the energy approach – how the breaking energy dissipation occurs in the surf zone. Many investigators were involved in formulating this phenomenon. For individual monochromatic waves, the two most well-knowns are: the one proposed by M.J.F. Stive in 1984 and the other one proposed by W.R. Dally, R.G. Dean and R.A. Dalrymple in 1985. It was the energy dissipation formulation by J.A. Battjes and J.P.F.M. Janssen in 1978 that addressed the energy dissipation processes of spectral waves. This formulation required an iterative process, and was therefore cumbersome to apply. However with the modern computing power, that hurdle does not exist any more. In addition to the aforementioned investigators, there are many others who modified and refined the formulations and understandings of the surf zone processes. In this piece let us attempt to see how the energy dissipation works for spectral waves. Among the coefficients influencing the energy dissipation is a factor that defines how fractions of the spectral wave group break. This factor is very important, and let my try to illustrate how that works – by solving the term iteratively. . . . Before doing that let me highlight some other understandings of the surf zone processes. Early investigators of the surf zone processes have noticed some important wave breaking behaviors – that all waves do not break in the same fashion and on all different beach types. Their findings led them to define an important dimensionless parameter – the Surf Similarity Number (SSN) – also known as the Iribarren Number (after the Spanish engineer Ramon Cavanillas Iribarren, 1900 – 1967; C.R. Iribarren and C. Nogales, 1949) – or simply the Wave Breaking Number. This number is the product of beach slope and wave steepness – and is directly proportional to the beach slope and inversely proportional to the square root of wave steepness (steepness is the ratio of wave height and wave length – long-period swells are less steep than short-period seas). Either of these two parameters could define a breaker type. To identify the different breaker types it is necessary to define some threshold SSN values. Among the firsts to define the threshold values were C.J. Galvin (1968) and J.A. Battjes (1974), but more lights were shed by many other investigators later. On the lower side, when the SSN is less than 0.5, the type is termed as Spilling Breaker – it typically occurs on gently sloping shores during breaking of high-steepness waves – and is characterized by breaking waves cascading down shoreward creating foamy water surface. On the upper side, when the SSN is higher than 3.3, the type changes to Surging and Collapsing Breakers. In a surging breaker, waves remain poorly broken while surging up the shore. In a collapsing breaker, the shoreward water surface collapses on the unstable and breaking wave crest. Both of these breakers typically occur in steep shores during periods of incoming low-steepness waves. When the SSN ranges between 0.5 and 3.3, the type becomes a Plunging Breaker – it typically occurs on intermediate shore types and wave steepness – and is characterized by curling of shoreward wave crest plunging and splashing on to the wave base. This type of breaker causes high turbulence, and sediment resuspension and transport on alluvial shores. An example of sediment transport processes and associated uncertainties in the surfzone is in the Longshort Sand Transport. . . . Perhaps it is helpful if we think more for a while, of what happens in the surf zone – as one watches the incoming waves – high and low – breaking at different depths propagating on to the shore. What prompts wave breaking? The shallow water wave-to-wave interaction – Triad lets wave spectrum evolve into a narrow band shifting the peak energy to high frequencies. The concentration of wave energies lets a wave-form to become highly nonlinear and unsustainable as the water particle velocity exceeds the celerity (square root of the product of acceleration due to gravity and depth), and right before breaking it takes the shape of a solitary wave (a wave that does not have a definable trough). I have tried to throw some lights on this breaking process in my short article published in the 2008 ASCE Journal of Waterway, Port, Coastal and Ocean Engineering {Discussion of ‘Maximum Fluid Forces in the Tsunami Runup Zone’}. Further, we have discussed in the Transformation of Waves piece on this page that a wave cannot sustain itself when it reaches the steepness at the threshold value of 1/7 and higher. A criterion proposed by Miche [Le pouvoir reflechissant des ouvrages maritimes exposes a l’action de la houle. 1951] captures the wave breaking thresholds not only due to the limiting steepness, but also due to the limiting water depths in shoaling water. In 1891, J. McCowan has shown that wave breaks when its height reaches 4/5th of the water depth on flat bottom. Now that we know the wave breaking types and initiation, let us try to understand how the energies brought in by the waves are dissipated. To illustrate the process I have included an image showing the percentage of fractional energy dissipation, as two spectral waves – a 2-meter 6-second and a 2-meter 12-second – propagate on to the shore. As demonstrated in the image, spectral waves begin to lose energy long before the final breaking episode happens. This means that the transformation process lets the maximums of the propagating spectrum to break as they reach the breaking threshold. In addition, as expected the shorter period waves (see the 6-second red line) lose more energy on way to the shallow water than the longer period (see the 12-second blue line) ones. By the final breaking, all the energies are dissipated giving births to other processes (water level change, nearshore currents and sediment transport). On a 1 to 10 nearshore slope, the SSN for the two cases are 0.5 and 1.1, respectively – indicating a Plunging Breaker type – but at two different scales. On most typical sandy shores, the long period waves are more likely to end up being a Plunging Breaker than the short-period ones. At the final stage, the breaking wave heights are 76% and 79% of water depths for the two cases. . . . Does anyone see another very important conclusion from this exercise? Well this conclusion is that, for any given depth and wave height the long-period waves bring in more energy to the shore than the shorter ones – the period effect. Let us attempt to see more of it at some other time. Some more insights on the surf zone waves are provided by Goda (Yoshima Goda, 1935 – 2012) describing a graphical method to help determine wave height evolution in the surf zone. His graphs show, for different wave steepness and nearshore slopes, how the maximum and the significant wave heights evolve on way from the deep water to the final breaking – and then to the reformed waves after final breaking. . . . . . - by Dr. Dilip K. Barua, 10 November 2016  In this piece let us talk about another of Ocean’s Fury – the Storm Surge. A storm surge is the combined effects of wind setup, wave setup and inverse barometric rise of water level (the phenomenon of reciprocal rise in water level in response to atmospheric pressure drop). Also important in the surge effects is tide because the devastating disasters occur mostly when the peak surge rides on high tide (the superimposition of tide and storm surge is known as storm tide). The wind setups as a minor contributor to water level rise occur in most coastal water bodies during the periods of Strong Breeze (22 – 27 knot; 1 knot = 1.15 miles/h; 1.85 km/h; 0.51 m/s) and Gale Force (28 – 64 knot) winds (see Beaufort Wind Scale) – during winter storms and landward monsoons – and are measurable when the predicted tide is separated from the measured water levels. Such setups and seiche (standing wave-type basin oscillation responding to different forcing and disturbances) are visible in water level records of many British Columbia tide gauges. Storms are accompanied by high wave activities, consequently wave setups are caused by breaking waves. Wave setup is the super elevation of the mean water level – this elevation rises from the low set-down at the wave breaker line. Let us attempt to understand all these different aspects of a storm surge – but focusing only on Hurricane (wind speed > 64 knot) scale storms. . . . I have touched upon the phenomenon of storm surge in the Ocean Waves piece on the NATURE page telling about my encounter with the 1985 cyclonic storm surge on Bangladesh coast. Later my responsibilities led me to study and model some storm surges – surges caused by Hurricane ISABELLE (CAT-2, September 18, 2003), Hurricanes FRANCES (CAT-2, September 5, 2004) and JEANNE (CAT-3, September 26, 2004), Hurricane IKE (CAT-2, September 12, 2008) on the U.S. coasts. Some materials of my U.S. experiences are presented and published (Littoral Shoreline Change in the Presence of Hardbottom – Approaches, Constraints and Integrated Modeling, FSBPA 2009; Sand Placement Design on a Sand Starved Clay Shore at Sargent Beach, Texas, ASBPA 2010 [presented by one of my young colleagues at Coastal Tech]; and Integrated Modeling and Sedimentation Management: the Case of Salt Ponds Inlet and Harbor in Virginia, Proceedings of the Ports 2013 Conference, ASCE). . . . In response to managing the storm effects, many storm prone coastal countries have customized modeling and study tools to forecast and assess storm hazard aftermaths. The examples are the FEMA numerical modeling tool SLOSH (Sea Lake and Overland Surges and Hurricanes) and GIS based hazard effects analysis tool HAZUS (Hazards U.S.). The SLOSH is a coupled atmospheric-hydrodynamic model developed by the National Hurricane Center (NHC) at NOAA. The model does not include storm waves and wave effects as well as rain flooding. NHC manages a Hurricane database HURDAT to facilitate studies by individuals and organizations. WMO-1076 is an excellent guide on storm surge forecasting. . . . What are the characteristics of such a Natural hazard – of the storm surge generating Hurricanes? The Hurricanes (in the Americas), Cyclones (in South, Southeast Asia and Australia) or Typhoons (in East Asia) are a tropical low pressure system fed by spiraling winds and clouds converging toward the low pressure. Perhaps an outline of some of the key characteristics will suffice for this piece.
Before going further an important puzzle needs to be highlighted. Both the short wave and the long storm surge wave are generated by the dynamic pressure or kinetic energy exerted by the speeding wind; and their magnitudes are proportional to the square of the speed (referring again to Daniel Bernoulli, 1700 – 1782). Why are there two different wave types? What are the processes responsible for their formations? The questions may sound naive, but the answers may reveal some valuable insights. The short wave is the water surface response to transporting the gained energy in progressive wave motions. Like the turbulent wind, these waves are highly irregular and spectral. The storm surge waves, on the other hand result from the hydrodynamic balance between the wind-induced water motion and the resistance of that motion by the coast. The result is the piling up of water at the coast – a standing long wave. One should not forget however that the transformation aspects of a long wave – the processes of funneling, resonance (note that a storm surge is not monochromatic, therefore some frequencies may resonate to the basin natural frequency) and shoaling also play a role. These processes affect the storm surge height in wide continental shelves and in closed basins, and are discussed in the Tsunami and Tsunami Forces piece on this page. To illustrate the storm surge, I have included an image of the CAT-1 Hurricane SANDY (October 29, 2012) storm surge on the New Jersey coast. . . . To manage this discussion into a short piece let us focus on a CAT-2 Hurricane characterized by a wind speed of 90 knot and a eye pressure of 970 millibar. Let us attempt to estimate some orders of magnitude of inverse barometric effect, wind setup and wave setup. Inverse barometric effect is often simplistically estimated as: 1 centimeter rise of water level in response to 1 millibar of pressure drop. For the example storm, the pressure drop at the center of the eye is 30 millibar – resulting in a reciprocal water level rise of 30 centimeter. This rise is rather like a moving dome of water having a typical diameter of some 30 kilometer. As one can imagine this simple estimate, however small that may be, cannot be added directly to the wind and wave setups because these two effects occur at the eye wall where wind speed is the highest. . . . How does the wind setup occur? Sustained winds cause a water surface drift current in the direction of the wind. For the example CAT-2 Hurricane, the surface drift current in absence of an obstruction would be about 1.4 meter per second. For a landfalling Hurricane, when the shoreward surface-layer current is obstructed by the coast, water level rises at the coast to balance and cause a seaward bottom-layer current (the generated bottom current erodes and transports sediments seaward changing the morphology of the coastal sea). A simple estimate shows that the example CAT-2 Hurricane would cause a wind setup of 2.7 meter for a 50 kilometer wide continental shelf with an average water depth of 10 meter. To give an idea of the wave setup let us consider a maximum significant wave height of 4.0 meter, and a maximum wave period of 14 second (these parameters roughly corresponds to those measured during Hurricanes FRANCES and JEANNE near the coast). An estimate shows that the wave setup is about 1.2 meter, about 30% of the wave height. In aggregate the storm surge for the example CAT-2 Hurricane is in the order of some 3 meter – likely less in some areas and more in others. The Hurricanes FRANCES, JEANNE, IKE and ISABELLE registered surge height of about 2.0 meter in some places. What is the periodic scale of a storm surge? For the slow moving Hurricanes like FRANCES and JEANNE, it was about 4 days (from the time of rising to the time falling at the same water level), and for Hurricane IKE it was 1.5 days. Note that the periodic scale of this size covers 2 or more tidal cycles – but the damages mostly occur when the surge peak coincides with high tide (even more so when coincides with spring tide). . . . The complicacy of storm surges can best be described by numerical modeling. But it is also possible to estimate the surge more elaborately as a function of distance and time. Apart from damages, structural destruction and dike overtopping and breaches, storm surges greatly change nearshore and beach morphology providing works for summertime waves to reshuffle and redefine them. What we have discussed so far is positive storm surge that occurs on the right side of a landfalling Hurricane in the Northern Hemisphere. A negative storm surge, popularly known as the Sea Level Blow Out – also occurs simultaneously on the left side. See more in the Frontal Wave Force Field in Force Fields in a Coastal System. We have discussed about the likelihood of enhanced storm activity with Warming Climate on the NATURE page and also on this page. The high storminess together with the accelerated Sea Level Rise is only inviting humans to realize the consequences of our actions and face Nature’s Wrath – perhaps to a degree that modern humans have not witnessed before. When I started this piece, I thought of writing it as a small one. Instead, I ended up spending more time on this, resulting in the usual 4 to 5 pages length. Well what can one do when materials are overwhelming? . . . . . - by Dr. Dilip K. Barua, 3 November 2016 |