Science and technology
working with nature- civil and hydraulic engineering to aspects of real world problems in water and at the waterfront - within coastal environments
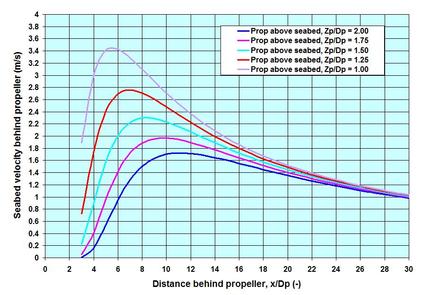 This topic is about the consequences of high turbulence and flow velocity that accompany a fixed-pitch screw propulsion ship. Propwash is the term used to describe the high exit velocity a propeller nozzle generates – and in the context of this piece – it is about the propwash effects on a marine terminal during the berthing and unberthing of a ship. The purpose of generating the high exit velocity by a ship is to cause equivalent forward thrust on it – with Newton’s (Isaac Newton, 1643 - 1727) Third Law of Motion in action. Screw propeller blades are twisted in such a way that a rotating propeller produces a high pressure difference by sucking in waters from one side and discharging them to the other to generate the exit velocity required to push a ship forward. The larger the DWT of a ship (see the Ship Motion and Mooring Restraints piece on this page for DWT) the higher is the requirement of propeller powers. But navy and coast guard vessels requiring high speeds, and Tugs tasked to haul barges or to maneuver large vessels during berthing and unberthing – however small they may be – also need to have high propeller powers. For navy and coast guard vessels – the high speed water-jet propulsion system is more of a requirement because the conventional screw propulsion system would just prove inadequate. Let me share some elements of this important port and maritime engineering topic in simple terms – focusing primarily on propwash and its effects. . . . Let me begin by focusing on engine thrust that moves a ship ahead. In still ambient water, propeller-induced thrust depends on three important factors – the product of these three describes the efflux – the exiting flux of water from the propeller nozzle. The first is the density of water – which means that with other factors remaining constant – a ship will have somewhat higher thrust in salt water than in fresh water (in addition a ship will feel somewhat lighter in salt water due to enhanced buoyancy). The second most important parameter – is the diameter of the propeller Dp – the thrust is proportional to the square of Dp, implying that it will increase by 4-fold if Dp is changed, let us say, from 1 m to 2 m. Actually, this dependence comes from the equation of the area of a circle – the area being proportional to the square of the diameter. The concept is utilized by encasing the propeller in a duct or short nozzle to obtain more power for the same engine rpm. Despite the engine thrust being highly dependent on the propeller diameter, there is a limit to its maximum size. One of the reasons is that the diameter must scale with the draft of the ship – otherwise a portion of the propeller will surface and rotate in air. But such surfacing cannot be avoided when a ship rides on rough seas with high roll and pitch motions. To describe the third important factor – one needs to take the help of Bernoulli Equation (Daniel Bernoulli, 1700 – 1782). As often pointed out in other pieces, the flow-induced dynamic pressure illustrated by Bernoulli is very important in fluid mechanics – this pressure is proportional to the square of the velocity. Here again, if the velocity is increased, let us say, from 1 m/s to 2 m/s, with other factors remaining constant, the thrust will increase by 4-fold. The exit velocity of an open propeller behaves in a certain way. At a distance of about 0.5*Dp behind the propeller, the exiting jet from an unducted propeller becomes constricted to Do = 0.7*Dp. The maximum jet exit velocity Uo occurs at this location with dissipation taking place further behind. Unlike the other two factors (water density and propeller diameter) – one does not know the jet exit velocity a priori. How to estimate it? To answer this question engineers had to conduct series of lab experiments. Delft Hydraulics took the pioneering role in this regard with HG Blaauw and EJ van de Kaa publishing their paper in 1978 – with more subsequent researches coming from other institutions. Remarkable among these, is a review made by MJ Prosser in 1986. Other notable titles dealing with analysis and design recommendations include: EAU (1996); PIANC (1997, 2002 and 2015), Port Designer’s Handbook: Recommendations and Guidelines (CA Thoresen 2003), Design of Marine Facilities for the Berthing, Mooring and Repair of Vessels (JW Gaithwaite 2004), The Rock Manual (CIRIA 2006), HJ Verheij and C Stolker (2007), and K Römisch and E Schmidt (2009). The first theoretical foundations of the behavior of an expanding jet came from ML Albertson and others (1948) and N Rajaratnam (1976). However despite nearly seven decades of scientific research and engineering, one is tempted to say that propwash and its loading on structures and seabed, and interactions – remain inadequately understood. In the simplest of all the known empirical relations, the exit velocity Uo is described empirically as the product of propeller revolutions per second n, Dp and a thrust coefficient Kt. The dependence on the thrust coefficient is somewhat weak – but a higher pitch (pitch is the distance traveled by a propeller in one complete revolution in no slip condition. Propeller blades are twisted to have a constant pitch from the root at the hub to the tip. The forward travel of a ship is however less than the nominal pitch determined at 0.7*R, R being the propeller radius. The difference is known as the slip. A note on propeller blade numbers – high numbers are usually optimally chosen to minimize vibration and noise.) ensures a higher Kt. Inclusion of Kt makes things somewhat circular – but to go around that, a rough estimate is possible without using Kt – and investigators have developed Kt tables/nomographs for ducted and unducted propellers as a function of the ratio of propeller pitch to its Dp. Another way to determine Uo is to use the applied engine power – and as can be understood, the applied power during berthing and unberthing is usually less than the capacity – varying from some 10% to 35% of the installed capacity. Once Uo is generated, the next important question is what happens to it away from the ship. The afterward behavior of Uo is important because loading on structural elements and seabed depends on it. In the zone of afterward established flow the efflux must mix and dissipate by expanding and entraining the ambient water into the jet boundary. Observations have indicated that in this zone, efflux expands like a cone at an angle of about 12 degrees around the core of maximum velocity. The velocity across the cone decreases from the center following the Gaussian distribution. Along the distance behind the propeller – the whole cone velocity decreases exponentially away from the propeller. At a certain distance behind the propeller, the expanding jet comes in contact with the seabed, causing scour when the sediment pick-up threshold is exceeded. . . . To illustrate the effects of an expanding jet on the seabed, I have included an image as an example – applicable for Dp = 2 m, n = 500 rpm, and Kt = 0.37. The estimated jet exit velocity Uo in this case is 16.2 m/s. The distance behind the propeller x and the height of the propeller axis above the flat seabed Zp are both normalized against Dp. The image shows how the jet velocity at the seabed increases and shifts toward the propeller as Zp decreases. At Zp/Dp = 1.0, the maximum is about 3.4 m/s. The change in Zp could occur, for instance due to the tidal rise and fall of water level, or to a small extent due to loading and unloading of a ship. In the example case, the maximum seabed velocities occurred at a distance x, from 5.3 to 6 times the Zp. The illustrated velocity is a time-averaged quantity – which means that instantaneous turbulence will likely register higher magnitude. Apart from turbulence, the second important one to cause higher velocity – is the effect of rudder behind a single propeller. The rudder splits the jet – and deflects it in one way or another depending on the ship’s heading requirement. At zero rudder deflection, the jet is split into two – one towards the water surface, the other towards the seabed – each making an angle of 12 degrees to the horizontal center – and each spreading at 10 degrees around the core. The implication of rudder deflection (maximum ~ 35 degrees) is that the jet-induced loading and scour phenomena could occur anywhere. The third is the twin-propeller setting with the rudder in the middle. The jets emanating from the two propellers are merged together at some distance (~ 10*Dp) behind the propeller. Unlike the rudder-behind single propeller setting, the deflecting power of the rudder is different, and the seabed velocity enhancement is expected to be less than the rudder-behind-a-single-propeller. However the propellers are often operated independent of each other, making predictions difficult. . . . Some other aspects of ship propulsion systems are also important. There are the thrusters – bow and stern – usually having smaller propellers than the main ones – because of this fact they generate less jet exit velocity. Bow thrusters have mostly a transverse setting – meaning that they draw waters from one side to discharge them to the other – to help sidewise maneuvering of the bow. They mostly have high Zp – thus their effects on seabed are not critical – however the horizontal jets could impinge on quay walls or piles to cause substantial loading. Stern thrusters are mostly omni-directional and are located close to the keel, so that their Zp is rather low. They can play a critical role on causing significant seabed loading and scour. Ship design and propulsion systems are continually evolving (such as podded propulsors, azimuth thrusters and water jets) requiring refinement of known relations, and finding new ones. The consequences of high speed water jet propulsion systems on structures and seabed, open a different dimension to the propwash and associated loading impacts. Apart from these ship-related factors, there are other factors related to the berthing structure – pile orientation, proximity of the sloped bank behind the piles, vertical face sheet-pile walls, etc. All these factors are likely to complicate the jet loading – making the search for critical design conditions difficult – but one thing is certain, it is the potential conditions of repeated loading and incremental progression of damages – that dominate all design and operational considerations. Protecting the seabed against scour-related undermining of the structure foundation for low underkeel clearance setting can be very expensive. For the illustrated case with the maximum seabed velocity of 3.4 m/s, the theoretical median rock diameter is about 0.9 m. Accounting for turbulence factor and other uncertainties associated with rudder, and structural proximity, etc. the required design median rock diameter is likely to be even higher. For such cases, scour protection by bare rock riprap layers can appear impractical. There is an additional danger – it is the sucking-in velocity caused by a propeller with low underkeel clearance, which could suck-in smaller size rocks into the propeller – damaging it. Alternatives such as insitu concrete (such as concrete mattress, grouted rock) and prefabricated mattress (such as concrete block mattress, asphalt mattress, gabion mattress) provide promising options. . . . Let me now briefly focus on another consequence of high jet exit velocity – and it is the drag force the velocity causes on piles supporting a berthing superstructure. To illustrate it simply, suppose there is an offshore marine terminal – a jacket structure standing on 20 m water. Together with dolphins, its purpose is to facilitate berthing, mooring and loading-unloading of oils or gas. A 10-m draft tanker berthing on this facility, likely un-assisted by Tugs, will berth and unberth at the same location repeatedly. If it is located in the Gulf of Mexico, with very little tidal range, it is highly likely that the tanker propeller jets will cause repeated drag loading at the same heights of the jacket-piles. For a case similar like this, the critical aspect is the localized repeated drag forces causing abrasion and bending of the piles. In this situation, the underkeel clearance is likely to be high; therefore any jet-induced seabed loading and scouring effect on the seabed may turn out to be negligible. . . . I like to stop at this – by finishing this piece with a tribute to Stephen Hawking (1942 – 2018) – who despite having debilitating illness did not stop from being active and pursuing his dream for finding a Unified Theory of Everything. He began the 1st paragraph of his book, A Brief History of Time with a little piece of humor: A well-known scientist (some say it was Bertrand Russell, 1872 – 1970) once gave a public lecture on astronomy. He described how the earth orbits around the sun and how the sun, in turn, orbits the centre of a vast collection of stars called our galaxy. At the end of the lecture, a little old lady at the back of the room got up and said: ‘What you have told us is rubbish. The world is really a flat plate supported on the back of a giant tortoise.’ The scientist gave a superior smile before replying, ‘What is the tortoise standing on?’ ‘You’re very clever, young man, very clever,’ said the old lady. ‘But it’s turtles all the way down!’ . . . . . - by Dr. Dilip K. Barua, 9 May 2018
0 Comments
|