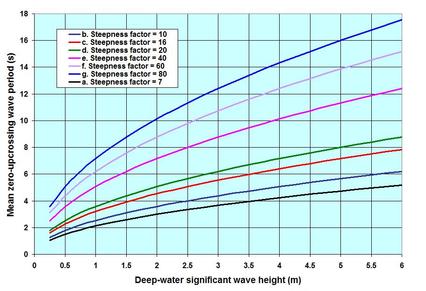
 Waves were the focus of discussions in at least 5 pieces on this NATURE page, and in 1 and more pieces on the SCIENCE & TECHNOLOGY page. I am tempted to add another piece – because understanding of the wave processes and their loadings and other effects on structures and seabed is very important – not only for coastal/hydraulic civil engineers but also for all. We have discussed in some other pieces that wave is the fundamental mechanism how energy is transformed and transported – in fluid flows, in climatic patterns and changes, in electro-magnetism, and in societal behaviors of plants and animals including humans. Sometimes when the wave length is too long – for example, in seasonal river flows which we tend not to consider as a wave – but the long-term behavior of a river and its alluvial morphology is better understood if the river seasonality is properly characterized. This piece is about 3 integral parameters of waves – the height (simply the height between successive crests and troughs), the period (simply the time lapse between two successive crests or troughs) and the length (simply the distance traveled by two successive crests or troughs), and the inter-relationships among them. These three parameters are integral – because they convey no indication of the shape of a wave – its symmetry or asymmetry. We have discussed in other pieces {Ocean Waves; Linear Waves; Nonlinear Waves; Spectral Waves; and Transformation of Waves} that Natural waves are irregular, random and spectromatic – and that they can be approximated as linear or nonlinear based on a single parameter – the Ursell Number (Fritz Joseph Ursell, 1923 – 2012). This parameter describes a threshold combining the two ratios H/d and d/L, and is given by U = HL^2/d^3 {H = wave height; d = water depth; L = local wave length; and T = wave period. For spectral waves, Hs = significant wave height, average of the highest 1/3rd of waves; Tp = wave period corresponding to the peak spectral energy}. It turns out that for all practical purposes, waves can be assumed to be symmetric or linear, when U is equal to or less than 5.0. . . . Perhaps it is helpful to begin with some principles of monochromatic wave as we move on to discussing Natural waves. Among the parameters, the wave period T and the wave length L are uniquely related via the celerity C – the propagation speed of the wave energy; L being the product of C and T. In deep-water with d/L ≥ 0.5, waves do not see the depth; therefore C is solely a function of T, with L becoming a function of T^2. One implication of this dependence becomes immediately clear – it is the decomposition of a spectromatic wave composite into its component frequencies – the longer period component having higher C, dispersing out from the shorter ones. This is how one explains the incoming swells arriving first on shores – as the precursor of a storm. With decreasing water depth, starting at d/L ≈ 0.05, wave attains the characteristic of a long wave or shallow-water wave, and C becomes a sole function of depth d. For C to go through the transformation (from independence to the dependence on depth), the wave period T must remain constant. In a chapter, Small Amplitude Wave Theory (Estuary and Coastline Hydrodynamics, ed. AT Ippen, McGraw-Hill, 1966), PS Eagleson and RG Dean demonstrated the necessity for constancy of wave period by considering a simple harmonic wave train as it moves from deep to shallow water. It is simply argued from the principle of the conservation of the number of waves propagating from one section to the next, that – it is either the wave period or the length that must change to ensure the continuity – since the wave length changes following the changing C, the period must remain constant. There is a transitional region between the deep (d/L ≤ 0.5) and shallow waters (d/L ≥ 0.05) where C depends on both T and d. These dependences make it difficult to determine L explicitly. In modern times with digital computation, that difficulty has been overcome. But a simple relation proposed by HN Hunt in 1979 yields values that are surprisingly close to the exact L. There is another aspect of wave length: what we have discussed so far is the linear wave length for U ≤ 5.0; in shallower water with higher U, the actual wave length (nonlinear) becomes longer, differing from L – the difference becomes wider as the wave propagates to increasingly shallow water. For example, for a 2-m high 8-s wave, at U ≈ 30.0, L = 57.5 m, Stokes 5th order L_5th = 60.2 m, the Cnoidal L_cnoidal = 68.9 m. While the relationship between wave period and length is simple, the same between wave height and period is not straightforward. The reason is that wave heights can be associated with a wide range of periods – as evident from the scatter diagrams one sees in observed Natural waves. They usually vary according to wave steepness – the steepness being the ratio of H/L – from (1/7 ≈ 0.143) to (1/80 ≈ 0.013). The first is the limiting high steepness – at and above which a wave cannot sustain itself and must break (the criterion proposed by R Miche 1944, 1951). The second represents roughly the limit of observed waves dominated by long-period swells in coastal oceans. . . . To demonstrate the wave height-period association of spectromatic waves, I have included an image showing the relationships between mean zero up-crossing wave period Tz and deep-water Hs – based on a relation proposed in my 2015 World Scientific paper: Longshore Sand Transport – An Examination of Methods and Associated Uncertainties. The family of lines for different steepness factors (reciprocal of steepness) shows the relationship from high steepness (line a) at the bottom to the low at the top (line g). For 1-m wave height, the period-envelop varies from 2.12 s to 7.16 s; for a 6-m high wave it is from 5.19 s to 17.53 s. What is the working relationship between Tz and Tp – the wave period of practical interest? Following CL Bretschneider (1969) – who has shown that, the square of the wave period follows the asymmetric Rayleigh distribution – the peak spectral period Tp ≈ 1.41Tz. Unlike the constancy of a single monochromatic wave period, Tp is not something that remains constant for a wave group – it evolves as the energy is transferred and redistributed within the group due to non-linear wave-to-wave interactions and other transformational processes – therefore the downstream peak spectral wave period is not same as the upstream. The identification of the physics of this interaction process is fairly new and has been attributed to the contributions made by Hasselmann and others (1985). Here are some explanations of the wave-to-wave interactions.
It is time to wrap this piece by exploring the mind of Spanish painter and sculptor Salvador Dali (1904 – 1989) . . . Have no fear of perfection – you’ll never reach it . . . Professional context? Imperfection – but of the learned mind to be meaningful and justifiable. . . . . . - by Dr. Dilip K. Barua, 20 June 2018
0 Comments
Leave a Reply. |

 RSS Feed
RSS Feed
