Science and technology
working with nature- civil and hydraulic engineering to aspects of real world problems in water and at the waterfront - within coastal environments
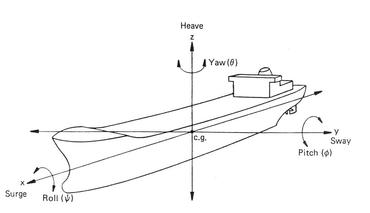 This topic represents one of the most interesting problems for port terminal installations – or in a broader sense for station keeping or tethering of floating bodies such as a ship (vessel) or a floating offshore structure. The professionals like Naval Architects and some Maritime Hydraulic Civil Engineers are trained to handle this problem. I had the opportunity to work on some projects that required the static force equilibrium analysis for low frequency horizontal motions, and the dynamic motion analysis accounting for the first order motions in all degrees of freedom. They were accomplished through modeling efforts to configure terminal and mooring layouts, and to estimate restraining forces on mooring lines and fenders for developing their specifications. Let me share some elements of this interesting topic in simple terms. To manage this piece to a reasonable length - some other aspects of ship mooring such as its impacts on structures during berthing are not covered. Hope to get back to this and other aspects at some other time. This piece can appear highly technical, so I ask the general readers to bear with me as we go through it. It is primarily based on materials described by American Petroleum Institute (API), Oil Companies International Marine Forum (OCIMF), The World Association for Waterborne Transport Infrastructure (PIANC), British Standard (BS), the pioneering works of JH Vugts (TU Delft 1970) and JN Newman (MIT press 1977), and others. Imagine an un-tethered rigid body floating in water agitated by current, wave and wind. These three environmental parameters will try to impose some motions on the body – the magnitudes of which will depend on the strength and frequency of the forcing parameters – as well as on the inertia of the body resisting the motion and on the strength of restoring forces or stiffness. . . . Before moving into discussing the motions further, a few words on current, wave and wind are necessary. Some of these environmental characteristics were covered in different pieces posted on the NATURE and SCIENCE & TECHNOLOGY pages. Among these three, currents caused by long-waves such as tide, are assumed steady because their time-scales are much longer than the ship motions. Both wave and wind, on the other hand are unsteady – and spectromatic in frequency and direction – causing motions in high (short period) to low (long period) frequency categories. In terms of actions, the ship areas below the water line are exposed to current and wave actions – for wind action it is the areas above the water line. Often the individual environmental forcing on the ship’s beam (normal to the ship’s long axis) proves to dominate the directional loading scenario. But an advanced analysis of the three parameters is required in order to characterize them as the combined actions from the perspectives of operational and tolerance limits – and for design loads acting on different loading faces of the ship. The acceptable motion limits vary among ships accounting for shipboard cargo handling equipments and safe working conditions. Some simple briefs on the oscillation dynamics. When a rigid body elastic system is forced to displace from its equilibrium position, it oscillates in an attempt to balance the forces of excitation and restoration. The simplest examples are: the case of vertical displacement when a mass is hanged by a spring, and the case of angular displacement of a body fixed to a pivot. When the forcing excitation is stopped after the initial input, an elastic body oscillates freely in exponentially diminishing amplitude and frequency. A forced oscillation occurs when the forcing continues to excite the system – in such cases resonance could occur. . . . The natural frequency (or reciprocally the period) of a system is its property and depends on its inertial resistance to motion, and on its strength to restoring it to equilibrium. The best way to visualize it is to let the body float freely in undamped oscillations. It turns out that the natural period is directly proportional to its size or its displaced water mass. This means that a larger body has a longer natural period of oscillation than a smaller one. Understanding the natural period is very important because if the excitation coincides with the natural period, resonance occurs causing unmanageable amplification of forces. In reality however, resonance rarely occurs because most systems are damped to some extent. Damping reduces the oscillation amplitude of a body by absorbing the imparted energy – partially (under-damped), or more than necessary (over-damped), or just enough to cause critical damping. Most floating systems are under-damped. Force analysis of an over-damped body requires an approach different from the motion analysis. . . . Here are some relevant terms describing a ship. A ship is described by its center-line length at the waterline (L), beam or width B (the midship width at the waterline), the draft D (the height between the waterline and ship’s keel), the underkeel clearance (the gap between the ship’s keel and the seabed), the fully loaded Displacement Tonnage (DT) – accounting for displacement of the ship with DWT (Dead Weight Tonnage – the displaced mass of water at the vessel’s carrying capacity – accounting for cargo, fuel, water, crew [including passengers if any] and food item storage), and the Lightweight (empty) Weight Tonnage (LWT). A vessel is known as a ship when its tonnage DWT is 500 or more. The ship dimensions are related to one another in some fashion allowing to making estimates of others if one is known. A term known as the block coefficient (CB) represents the fullness of the ship – it is the ratio of the ship’s actual displaced volume and its prismatic or block volume (with L, B and D). The typical CBs are 0.85 for a tanker and 0.6 for a ferry. To give an idea, the new Panamax vessel (maximum allowed through the new Panama Canal Lock) is L = 366 m; B = 49 m, and D = 15 m. Different classification societies like ABS (American Bureau of Shipping) and LR (Lloyd’s Register of Shipping) set the technical standards for the construction and operation of ships and offshore floating structures. . . . What are some of the basic rigid body motion characteristics? The floating body motions occur in six degrees of freedom representing linear translational and rotational movements. Literature describes the six motion types in different ways; perhaps a description relying on the vessel’s axes is a better way of visualizing them. All the three axes – the horizontal x-axis along the length, the horizontal y-axis across the width, and the vertical z-axis originate at the center of gravity (cg) of the vessel. To illustrate them I have included a generic image (credit: anon) showing the motions referring to:
. . . Another important understanding needs to be cleared. This is about the stability or equilibrium of the vessel for inclinational motions. A floating body is stable, when its centers of gravity (cg) and buoyancy (cb) lie on the same vertical plane. When this configuration is disturbed by environmental exciting forces like wind and wave, or by mechanical processes like imbalanced loading and unloading operations, the vessel becomes unstable shifting the positions of cg and cb. The imbalanced loading can only be restored to equilibrium by the vessel operators by re-arranging the cargo. Among others, the vessel operators also have the critical responsibility to leave the berth during a storm, to tending the mooring lines – so that all the mooring lines share the imposed loads – and in keeping the ship within the berthing limit. For non-inclinational motions like surge, sway, heave and yaw the coincidental positions of the cg and cb are not disturbed. They just translate back and forth in surge, and near and far in sway oscillations. In heave and yaw, the coincidental positions of cg and cb do not translate – for heave it is the vertical up and down motion, and for yaw it is the angular translatory motion about the vertical axis. . . . How to describe these motions and the corresponding forces in mathematical terms? The description as an equation is conceived in analogous with the equilibrium principle of a spring-mass system – where an oscillating exciting force causes acceleration, velocity and translation of the floating body. For each of the six degrees of freedom, an equation can be formed totaling six equations of motion. With all the six degrees of freedom active, the problem becomes very formidable to solve analytically; the only option then is to resort to numerical modeling technique. Motion analyses are conducted by two different approaches – the Frequency Domain analysis focuses on motions in different frequencies, adding them together as a linear superposition. The Time Domain analysis on the other hand focuses on motions caused by the time-series of the exciting parameters. Perhaps some more clarifications of the terms – the mass including the added mass, the damping and the stiffness – are helpful. The total mass (kg) of a floating body comprises of the mass of water displaced by it, and the mass of the surrounding water called the added mass – which is proportional to the size of the body, and also depends on different motion types. These two masses resist the acceleration of the body. The Damping (N.s/m; Newton = measure of force; s = time, second; m = distance, meter) is a measure of the absorption of the imparted energy by the floating system – having the effect of exponentially reducing its oscillation. Damping is three basic types: damping by viscous action, wave drift motion and mooring system restraining. The stiffness (N/m) is the force required of an elastic body to restore it to the equilibrium position. The terms discussed above refer to rectilinear motions of surge, sway and heave. How about the terms for angular motions of roll, pitch and yaw? The total mass for angular motions becomes the mass moment of inertia, and the stiffness is replaced by the righting moment (moment is the product of force and its distance from the center). In the cases of environmental and passing vessel excitations, gravity and mooring restraints try to restore the stability of the vessel. The roles of these restoring elements are like this:
A few words on the passing vessel effect. A speeding vessel passing past a moored vessel causes surge and sway loads and yaw moment on the latter. The magnitudes of them depend on the speed of the passing vessel, the distance between the two, and the underkeel clearance of the moored vessel. As a simple explanation involving the ships in a parallel setting: a moored vessel starts to feel the effect when the passing vessel appears at about twice the length of the former, and the effect (push-pull in changing magnitude and phase) continues until cleared of this passing away distance. Analysis shows that sway pull-out is the highest when the passing vessel is at the midship of the moored vessel – but the surge and the yaw are the lowest at this position. . . . Well so far so good. On some aspects of mooring now. Mooring or station keeping comprises of two basic types – fleet and fixed moorings. The former refers to systems that use primarily the tension members such as ropes and wires, and is mostly applied in designated port offshore anchorage areas. Ports have designated outer single-point anchorage areas where ships can wait for the availability of port berthing, and/or for loading from a feeder vessel and unloading to a lighterage vessel. The area is also used to remain on anchor or on engine-power during a storm. Ships can cast anchors in those areas or moor to an anchorage buoy. For a single point mooring on anchor a large mooring circle is needed to prevent the anchored ship from colliding with the neighbouring vessels. Assuming very negligible drifting of the anchor, the radius of this influence-circle depends on water depth, anchor-chain catenary and ship’s overall length. Anchoring to a moored buoy by a hawser reduces this radius of influence-circle of the moored ship. Buoy facilities are usually placed offshore for mooring of tankers, and such buoys are equipped with multiple cables and hoses to cater to the logistical needs of the vessel as well as for loading and unloading petroleum. A vessel moored at a single point is free to swing or weather-vane following the prevailing weather and current to align itself bow-on. The weather vaning is advantageous because it minimizes the vessel area exposed to wind, wave and current loads. Fixed Mooring refers to a system that uses both tension (ropes and wires) and compression members (energy absorbing fenders). A different type of fixed mooring, mostly implemented in rather calm environmental settings of current and wave is implemented in marinas. The floats of marinas are usually anchored via collars to vertical mono-piles. Only a single-degree of freedom is provided in this system – which means that the floats move rather freely vertically up and down with changing water levels. Typical fixed moorings include tying the ship at piers (port structures extending into the water from the shore), wharves (port structures on the shore), and dolphins (isolated fixed structures in water) together with loading platforms. The latter is mostly placed in deepwater by configuring the alignment such that moored ships will largely be able to avoid beam seas, currents and wind. The tying is implemented by wires and ropes – some are led from the ship winches through fair leads to the tying facilities like bollards, bitts or cleats on the berthing structures. Wires and ropes are specified in terms of diameter, material, type of weaving and the minimum breaking load (MBL). The safe working load (SWL) is usually taken as a fraction of MBL - some 0.5 MBL or lower. The mooring lines are spread out (symmetrically about the midship) at certain horizontal and vertical angles. Typically, the spring lines (closed to midship mostly resisting the longitudinal motions) spread out at an angle no more 10 degrees from the x-axis; the breasting lines (between spring and bow/stern lines, mostly resisting the lateral motions) spread out at an angle no more than 15 degrees from the y-axis; and the bow and stern lines are usually laid out at 45 degrees. The maximum vertical line angles are kept within 25 degrees from the horizontal. The key considerations for laying out mooring lines are to keep spring lines as parallel as possible; and breast lines as perpendicular as possible to the ship’s long axis. When large ships are moored with wires, a synthetic tail is attached to them to provide enough elasticity to the vessel motions. . . . This piece ended up longer than I anticipated. Let me finish it by quoting Nikola Tesla (1856 – 1943) – the famous inventor, engineer and physicist: If you want to know the secrets of the universe, think in terms of energy, frequency and vibration. . . . . . - by Dr. Dilip K. Barua, 15 September 2017
0 Comments
Leave a Reply. |