Science and technology
working with nature- civil and hydraulic engineering to aspects of real world problems in water and at the waterfront - within coastal environments
 Coastal water is a showcase of the highly dynamic processes associated with the continuous rise and fall of water elevations – in symmetry and asymmetry. Apart from the undulations people see when sitting on a coastline – the best quantitative depiction of the showcase is revealed in time-series measurements of Water Level (WL) in many gaging stations that dot coastal waterfronts. The coastal zone WL on our Seashore – are driven by many – from regular Ocean Waves and Surf Zone activities to the episodic forcing of Storm Surge, Tsunami and Coastal Responses to Tsunami.
The Natural World of Coastal Water working under the canopy of the Gravitational Force Field or GFF is a superimposition of 5 other major Force Fields – the strengths of which vary in time and space. As described in the Force Fields in a Coastal System – they are: Metocean Force Field or MOFF; Extraterrestrial Force Field or ETFF; Land Drainage Force Field or LDFF; Heat Exchange Force Field or HEFF; and the Frontal Wave Force Field or FWFF. All these force fields have different magnitudes and scales of variation. Depending on what dominates a certain scenario – a water body responds by displaying its flow characteristics transformation dynamics. Effects of MOFF, ETFF, LDFF and FWFF are highlighted in this essay. The role of HEFF in WL changes is not so much of a significance like others, therefore not discussed. Linearity, Non-linearity, Spectromatic and Turbulent compositions of water motion with its characteristic Wave Asymmetry and associated Coastal Ocean Currents – in areas from Coastal River Delta and Coastal Inlets to the contiguous ocean – generate many other processes and activities on alluvial seabeds that include: Sediment Transport, Longshore Sand Transport and Sedimentation, among others. In the presence of coastal structures – such as Breakwaters, Flood Barriers and others – more activities follow – such as Wave Loads on Vertical Piles, Wave Structure Interactions and Scour, Forces on Structures—thereby causing Motion on Moored Ships and Propwash in harbors. . . . With this, let us attempt to see in brief terms – how the interesting dynamics of WL change works in the coastal zone. The processes related to this changes are described from the viewpoints of Force Fields - and the pasted image is created from that perspective. My long experience in coastal engineering as well as my publications and teaching lecture notes, together with several pieces posted in WIDECANVAS – helped me drawing up this essay. . . . 1. The Hydraulics of Coastal Water The WL rise and fall is a visual manifestation of the dynamic interactions between potential energy (proportional to the mass of the water column) and kinetic energy (proportional to water density and the mean flow velocity squared). The dynamic interactions between the two – a result of the changes in depth and topographical configuration – is superbly demonstrated in the fluid flow Bernoulli Equation (Daniel Bernoulli, 1700 – 1782). This equation is a simplification of the elaborate Navier-Stokes Equation (French engineer Claude-Louis Navier, 1785 – 1836; and British mathematician George Gabriel Stokes, 1819 – 1903) and Newton’s Law of motion (Isaac Newton, 1642 – 1727). The Seabed Roughness of Coastal Waters shows the practical interpretations and significance of different terms in the Navier-Stokes Equation - further in the Natural Equilibrium and Water Modeling essays. Bernoulli Equation representing steady approximation of long-wave transformation – is a clear depiction of the equilibrium correspondence between the potential energy or static pressure – and the kinetic energy or dynamic pressure in a frictionless flow. In other words – when flow velocity becomes high, the water level is lowered and vice versa. ETFF The regular rise and fall of coastal WL represents a superposition or phase-addition of multiple forcing factors – among them ETFF is overwhelmingly dominant. The undulation manifests itself in semi-diurnal (like in North America East coast), diurnal (like in Gulf of Mexico coasts) and mixed tides (like in North America West coast). The different tidal types are the results of interactions between the forced ocean tide and the coastal zone topographical factors. Diurnal tides are usually low in amplitude. The fortnightly spring and neap tides responding to the waxing and waning phases of moon – is another regular forcing added on top of the daily tide. Tide is a predictable quantity. Harmonic analyses of measured tidal heights at a certain station are used to determine constituents and arguments of the moon-sun phases and forces – which are then used to predict future tide at that station. That’s how regional and global tide tables are produced and published – to help all navigators and different works in coastal waters, ports and harbors. As highlighted in Ocean Waves – the coastal tide resulting from the circumnavigating ocean tide that traverses close behind the trio of the Sun-Moon-Earth phase – goes through the transformation processes of shoaling, funneling, amplification-or-weakening, and near-resonance amplification in the coastal zone. The phenomenon and processes of near-resonance amplification are demonstrated in my 2006 Tsunami Modeling paper. In especial coastal configurations, amplifications give birth to coastal overtides and compound tides (demonstrated in my 1991 COPEDEC-PIANC paper – Fourier Spectral analyses of time-series water levels showed how some harmonics were amplified, others were weakened in simultaneous observations along the Bangladesh coast). Coastal WL displays a Gaussian bell-shaped curve – a symmetric distribution about the mean (more in Uncertainty Propagation in Wave Loadings). As demonstrated in The World of Numbers and Chances – such a distribution helps one to find the exceedence probability of WL for a certain height. As discussed further later, this probability is very useful to engineer the crest or the top elevation of a coastal structure. Apart from WL descriptions as such – local WL variations do occur in different frequencies, amplitudes and phases, in particular when MOFF, LDFF and FWFF dominate the regional hydrodynamics. Nature of these force fields and consequences are described in the Force Fields in a Coastal System essay – with the following descriptions heavily relying on what were written there. MOFF Apart from generating surface wave activities (see Wave Hindcasting), MOFF actions display one of the devastating Ocean’s Fury on coastal WL – the Storm Surge – a virtually troughless wave crest that flood coastal low lands – propagating onto coastal inlets and estuaries. It is the combined effects of wind setup, wave setup and inverse barometric rise of WL (the phenomenon of reciprocal rise in water level in response to atmospheric pressure drop). MOFF effects are modulated by tidal activities and phases on a rather daily basis – accentuating or attenuating WL. In terms of the storm surge – the devastating disasters occur when the peak surge rides on high tide (the superimposition of tide and storm surge is known as Storm Tide). The wind setup contribution to WL-rise in most coastal water bodies – occurs during the periods of Strong Breeze and Gale Force winds (see Beaufort Wind Scale) – and during the passing episodes of winter storms and landward monsoons. They are measurable when the predicted tide is separated from the measured WL. Such setups and seiche (standing wave-type basin oscillation responding to different forcing and disturbances) are visible in WL records of many British Columbia tide gages. When Hurricane-scale cyclonic wind fields dominate a certain area – wind-setup and set-down turn into surge waves attaining the dynamics of a FWFF. The surge waves are characterized by high surge on the right side of the propagating storm in the Northern Sphere – with the negative surge on the left side. Affected by coastal topography – spectacular Sea Level Blow Out or emptying of water-basins could occur on the left side. A storm surge period scaling in order of days – causes devastating effects together with heavy rainfall – during the passage of a slow moving Hurricane than a fast moving one. Storms are accompanied by high wave activities, consequently wave setups are caused by breaking waves. Wave setup is the super elevation of the mean WL at the shoreline – this elevation rises from the low set-down at the wave breaker line. A model simulating the likeness of Hurricane FRANCES and JEANNE on Florida coast – that generated a 4.0 m high significant wave height having a peak spectral wave period of 14 second – the modeled wave setup was estimated to be about 1.2 meter, or about 30% of the wave height. LDFF This force field is a minor contributor to coastal WL changes. It particularly affects the deltaic estuaries (Coastal River Delta) and the contiguous coastal ocean when high river stage wet season or storm season freshwater flow debouches into open water. Apart from the freshwater discharge volume – the density difference between the incoming flow and the ambient saline water – distorts local tide causing the mean water level to rise in the affected area. Seasonality of the freshwater outflow has a substantial influence on the river-mouth hydrodynamics – from pushing the freshwater front out into the sea during the high-flow period – to the modification of tidal wave – to letting salt-water to intrude into the lower river reaches during the lean-flow period. All these are manifested in WL changes. FWFF In the Force Fields in a Coastal System, I have tried to explain how FWFF works – in particular during the windstorm and tsunami episodes when depth-induced wave-breaking occurs. The same happens with tidal bores and in Surf Zone processes. FWFF is characterized by wave energy propagating in the supercritical flow regime. As visibly spectacular in tsunami and tidal bores – a wave with such a high speed could propagate upstream, and cross and overtake obstacles and transports huge load of debris and sediments. As a consequence of and immediately following the passing of the wave-front – the WL is raised. Tidal bores form during spring tides when the range is the highest. With the combined affects of shoaling and funneling – the propagating tide becomes highly asymmetric so much so that at a certain time maintaining the wave-form becomes unsustainable – the result is the breaking of the accumulated pressures – giving birth to tidal bores. Like all waves, a small tsunami in deep water shoals to monstrous waves as it propagates into the shallow water. After breaking, Tsunami Run-ups flood coastal lands with enormous inbound and outbound speeds causing havoc and destruction. The arrival of Tsunami crest is preceded by the huge draw down or Sea Level Suck Out associated with the Tsunami trough. This phenomenon sucks out things from the shore out into the sea—exposing shoreline features – leaving many aquatic lives stranded in air. . . . 2. Measuring Water Surface Elevation The WL is a depiction of the depth of the column of water – with or without the propagation of energy through it. How to have a quantitative measure of this water? The vertical measures of the column – are known as Depth when measured from top to bottom; and Height when measured from bottom to top. There have been enormous progress in hydrographic and oceanographic instrumentation of data collection- the following is only a basic snapshot. Depth measurements range from the past techniques of using marked vertical rods or strings – to the use of modern echosounder transducer probes immersed at a certain depth. Some echosounders also come with dual frequency option to determine the thickness of seabed fluid-mud layer, if present. A remarkable breakthrough in mapping the seafloor – is obtained by applying simultaneous use of multiple beam echosounder or sonar. The 2015 NOAA Newsletter Version says: Multibeam sonar has several transducers that allow a large swath of area to be surveyed at once making surveying much faster and more accurate . . . The swath width is determined by the depth of the seafloor being surveyed. The ping is emitted in a fan shape outward from the transmitter. The farther away the object the more area there is for the sound to echo off. The sonar pings several times per second which, with the speed of the boat, determines the horizontal resolution of the images created. A pressure sensor immersed at a certain location of the water column – yields the height of water above that sensor. On most occasions, the adjustment and tuning of the sensor registration frequency – allows one to measure both water and wave parameters. Among others, remote sensing technology is gradually replacing the traditional methods of hydrographic data collection. Two of them are highlighted – Lidar and Satellite Altimetry. LIDAR – the Light Detection and Ranging method uses light in the form of a pulsed laser to remotely measure distances from an airborne platform to the object – to map the reflecting land surfaces and underwater topography. A Lidar device consists of a laser, a scanner, and a specialized GPS to collect geospatial data. To avoid moisture absorption – a surface topographic Lidar typically uses a near-infrared laser to map the land on cloud-free days and nights – while a bathymetric Lidar uses water-penetrating green radiation to map seafloor elevations. In both the cases, the travel time taken by emission and reception along with the speed of the used laser beams – is used to calculate distance. More in NOAA Lidar Technology and Applications and USGS Lider Base. Satellite Altimetry – according to a NOAA article, satellite radar altimeters measure the ocean surface height (sea level) by measuring the time it takes a radar pulse to make a round-trip from the satellite to the sea surface and back. NOAA ongoing research shows that – the same principle can be used to estimate deep ocean floor elevations based on the principle that a seabed height difference can change the water surface elevations. The approach is complemented by employing multi-beam echosounders. . . . As outlined before, gaging stations installed in different waterfront locations – are used to serve many purposes, the most important of which is to measure water elevation with respect to a common vertical Datum. When bathymetry is related to the same vertical datum – seabed level appears – shown as positive for submerged seabed below the datum and negative as a drying height above the datum. What are the common datums used to determine coastal water elevation? Let us have a brief overview of them. A coastal engineer or a scientist comes across two vertical datum types – the Geodetic Datum and the Hydrographic or Chart Datum. Geodetic Datum. In North America, the Geodetic Datum is known as the North American Vertical Datum of 1988 (or NAVD88) – it replaced the formerly used National Geodetic Vertical Datum of 1929 (or NGVD29). While the conversion between the historical and presently used geodetic datums – varies spatially – USGS suggests this conversion: NGVD29 = NAVD88 – 3.6 ft (1.1 m), with an accuracy of (plus or minus) 0.5 ft. It means the NAVD plane is lower than NGVD. For example, if NGVD at a certain location is 1.0 m, the NAVD in that location would be 2.1 m. In coastal Washington State close to Canada border, NAVD plane is 1.23 m lower than NGVD. NGVD is approximately close to Mean Sea Level (MSL), but they are not exactly the same. Hydrographic or Tidal Datum. Tidal datums are based on the average of observations over a 19-year period – the so-called Metonic Cycle or NTDE (National Tidal Datum Epoch). This period is applied in defining: MSL (the arithmetic mean of hourly heights observed over the NTDE period); MLLW (Mean Lower Low Water; the arithmetic mean of the lower low water levels of the tide observed over the NTDE period); and MLW (Mean Low Water; the arithmetic mean of the low water heights observed over the NTDE period). The datum of Tide Tables and the bathymetric charts is MLLW on the West Coast (a mixed tidal regime). On the East Coast it is MLW (a semi-diurnal tidal regime). More in the NOAA Datum Definition. The MLW or MLLW are used to reduce and refer the measured depths and Tide Tables to Chart Datum. In North America, the traditional horizontal or georeference system was based on NAD83 or WGS84. With the advances in instrumentation, particularly GPS, some limitations and errors of the system have become evident. GPS is a three-part system: satellites, ground stations, and receivers. The trio works by some georeferenced ground stations monitoring the satellites to determine their locations. A receiver uses the signals from the satellites to locate its position in the referred system. The new georeference system in North America is called ITRF or the International Terrestrial Reference Frame. . . . 3. Sea Level Rise and Consequences How does Warming Climate going to affect coastal water level? Answer to this question is addressed in Sea Level Rise and Sea Level Rise Consequences. According to the 2021 IPCC - AR6, present rate of global mean sea level rise is 3.2 to 4.2 mm/year. In regional to global scales, the primary factors responsible for Sea level Rise (SLR) are attributable to: (1) melting of continental and polar ice masses; (2) reduction in ocean water density and resulting expansion; (3) ocean circulation responsible for distributing heat and dissolved substances; (4) isostatic rebound of the coastal landmass resulting from melting and regression of glaciers; (5) uplift or subsidence due to tectonic activity; (6) soft sediment consolidation and subsidence; and (6) ocean-atmosphere interaction. SLR is a slow process from an engineering point of view – yet, all low-lying coastal lands, waterfront engineering interventions and structures are vulnerable to its influence and effects. The vulnerability becomes clear if we consider the highlighted Force-Fields – which are going to become more forceful both in terms of intensity and frequency. This means planning and design factors and methods including design Standards and Codes would require redefinition and re-visitation to examine their adequacy to withstand the enhanced forces. The associated increase of Risks has a far reaching implication in all areas of coastal activities including the low-lying lands subjected to heavy rainfall and drainage flows. One reason is the depth-limited filtering of wave actions – for a certain depth only waves smaller than about 4/5th of water depth could pass on to the shore without breaking. Therefore, as the water level rises with SLR, the number of waves propagating on to the shore would increase. . . . 4. Water Level and Coastal Structure WL associated factors of inundation, runup and overtopping (green and spray) – constitute some of the pressing issues in planning and designing of coastal structures (more in Flood Barrier Systems). Still Water Level (SWL) together with the actions of a certain design wave – is used to design the top elevation of a coastal structure. Depending on location and importance, the raised WL caused by episodes of storm surge or tsunami is added to determine the Design Water Level (DWL). The determined top elevation is further fitted with a safety freeboard (the height of the structure above DWL) to minimize or eliminate the incidences of wave overtopping. Considering the structure type and installations - a Risk Analysis may be warranted to design final structure dimensions and risk implications. Large vertical-face coastal structures – are required to be fitted with wave absorption measures to minimize wave-structure interactions, reflection and turbulence. Placing frontal stone ripraps is one of the methods to absorb incident wave energy as well as to prevent structure toe scour. Such structures are usually aligned in mild outer bends to avoid inviting concentration of wave energy or wave focusing. More on coastal structures are in Civil Engineering on Our Seashore. Further in: USACE EM 110-2-1100 (Part VI series); USACE EM 1110-2-1415; USACE EM 1110-2-1913; Storm Surge Analysis and Design Water Level Determinations, USACE EM 1110-2-1412; USACE, Hurricane and Storm Damage Risk Reduction System Design Guidelines; and the 2008 TUDelft (VSSD) Breakwater and Closure Dams (2nd ed). In Breakwater engineering – the vertical height of the structure is designed differently according to WL and wave loading considerations. According to CIRIA (1991): Zone I – the bottom foundational zone below the level of Mean Low Water (MLW); the Zone II – the tidal zone from MLW to the Mean High Water (MHW), loading on this zone is very frequent and determines the longterm structural stability; the Zone III – the higher high water zone from MHW to the design level, wave attack on this zone is less frequent but of high impact; and the top Zone IV subjected to the effects of runup and overtopping. As in Wave Structure Interactions & Scour, Overtopping discharge rate is directly proportional to the incident wave height and period, but inversely to the freeboard. To give an idea: for a 1 m high freeboard, 2 to 1 sloped structure – a 1-m high wave with periods of 6-s and 15-s would have an overtopping discharge of 0.10 and 0.82 m^2/s per meter width of the crest, respectively. If the freeboard is lowered to 0.5 m, the same waves will cause overtopping of 0.26 and 1.25 m^2/s/m. In maritime port engineering – the determination of an appropriate COPE gets attention. Cope refers to top edge level of a quay or jetty adjacent to a berth. To understand the methods of determining Cope, one can consult: JW Gaythwaite 2004, Design of Marine Facilities for the Berthing, Mooring, and Repair of Vessels, ASCE Press, 2nd ed.; CA Thoresen 2003 Port designer’s handbook, Thomas Telford; and Y Goda 2000, Random Seas and Design of Maritime Structures, World Scientific. The optimum level of a cope can be selected by determining the risk of flooding together with an economic analysis. A low cope may be appropriate at berths exclusively used by small crafts. At cargo berths within an impounded dock the ground surface should be at least 1.5 m above the working water level. For berthing in open water harbor or exposed location, a statistical analysis can best be prepared to determine the level of the frequency of high water levels and wave heights. . . . This is the 82nd essay in WIDECANVAS – and is dedicated to a healthy ocean and coastal water – vital for our collective prosperity and sustaining a balance between Nature and a neat social cohabitation. It is in everyone’s interest that global awareness prevails – for a harmonious sensible management, in harnessing coastal and ocean resources – and in engineering interventions. It is a belated post to honor the World Oceans Day – the June 8th of each year. . . . The Koans of this piece: In a un-interrupted Natural world of interdependence and harmonious plays of the Fluid, Solid and Life Systems – how can anyone miss seeing the balancing acts of the rise and fall of wave dynamics in everything. Why wasting energy and resources to identify oneself and things as Conservative or non-Conservative through the media-articulated divisive lenses – how about something different – something that can be termed as being Realist, Simple, Right, Beneficial and Inclusive. . . . . . - by Dr. Dilip K. Barua, 4 October 2024
1 Comment
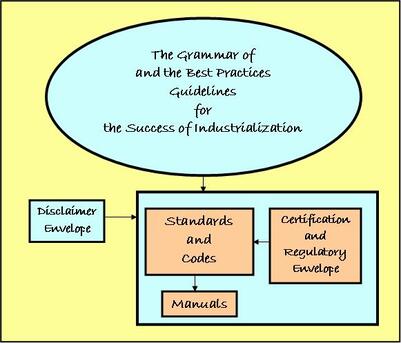 Given a mechanical civilisation the process of invention and improvement will always continue, but the tendency of capitalism is to slow it down, because under capitalism any invention that does not promise fairly immediate profits are suppressed. This saying of George Orwell (1903 – 1950) touches upon some very important issues associated with industrialization (mechanical civilisation) and capitalism. They are – the potential for unstoppable forward march of industrialization and some inhibitive effects of capitalism on it. In modern understanding, capitalism is an immediate profit making system in which the investor of the capital (primarily meant to be private) owns the enterprise – utilizing the services of machines and human labor. The human labor force that contributes to building up the capital - is not entitled to claim any share of the enhanced capital - it is only the executives who can claim so - the reward to them comes in the guise of shares, generous contract packages and hefty bonuses.
In this essay - I like to lay down some contexts first that are very much needed to understand the evolution and definition of the engineering standards, codes and manuals. These something are an important grammar for the initiation and sustenance of industrialization. . . . 1. The Birth of Modern Capitalist Processes The general principle of capitalism – perhaps without so much forceful emphasis on immediate profit making – is the earliest form of doing trades and commerce in human history. In earlier times, in all cultures ideas like harmony (some terms like sustainability were not vogue then) and symmetry were thought important for a healthy society (although one can argue whether such a healthy society was ever achieved). But as we shall see later, the 18th century definition of capitalist economy by Adam Smith (1727 – 1790) – twisted this term giving it a meaning that gave impetus to myopic view, shortsightedness and selfishness – stoking mistrusts and animosity among individuals with different perpetual stresses afflicting them – that result in the meandering outbursts of f-word, flash anger, cursing and violence. A 20th century American economist – Milton Friedman (1912 – 2006) gave further boost to Adam Smith’s theory by proposing the so-called Friedman Doctrine in 1970. It says . . . there is one and only one social responsibility of business – to use its resources and engage in activities designed to increase its profits . . . He further stressed that businessmen with a social conscience . . . are unwitting puppets of the intellectual forces that have been undermining the basis of a free society . . . In this doctrine the definition of social responsibility is twisted – in order to justify the triumphant victory of money-making freedom. With such definitions that reinforced the forces of modern capitalism – the vicious dog-eat-dog-world is unleashed – and turned governing democracy into capitocracy. Does this system deliver better than others? This end-result competence question must not be asked - instead, one must applaud and talk about the democratic processes - conceived and overwhelmingly dominated and controlled by corporate elites, lawyers and very loud media. In recent times with the unregulated and unguarded internet dependent communications and activities (see Artificial Intelligence - the Tool of No Limit) - the works of bad actors - have only been proliferating many times. Realizing the importance of the capitalist context of industrialization – let us attempt to delve further into it in simple terms – through the lens of critical thinking, so to say – because it is necessary to orient ourselves to the true perspectives associated with this topic. First, it is interesting to note that the immediate profit making – fits right into a democratic politician’s narrative – because his or her political lifetime and thinking revolves around short time scales from one election to another. One may, therefore infer that modern democracy – representing nothing more than party dictatorships rotating every few years – is perhaps the right tool to promote capitalism – because politicians can brag and campaign about how many material gains (even the bad ones – that become apparent in later times - and are gained at the expense of tax-payers) they made during their tenure. Further, the philosophy of large international financial institutions like IMF and World Bank also fits right into this paradigm – because they press and put conditions on poor countries (who appeal for help to ride over difficult times and alleviate debt servicing) to minimize costs for immediate profit making – by cutting wages and benefits to the hard working labor force, or sell state-owned enterprises to private ownerships. The rationale of Orwell observation can simply be outlined like this. Some industrialization processes of innovative and humane nature (such as extensive basic research; scientific exploration; nature, wildlife and environment protection, public welfare and health care; etc) that do not promise immediate profit (in monetary terms, but profits in terms of longterm benefits and others do accumulate) – largely remain outside the interest areas of capitalist enterprises. It also says why a capitalist system pampers majority (having an eye on large consumer base and labor force) – ethnic, religious or otherwise – by downplaying and ignoring the equal rights for minorities - more so for minority of minorities. Although governing principles of any country spell out equality in paper. Or, why some communities brag about or campaign for demographic changes in their favor – to implant longterm changes in a society. His observation also implies – why significant impact making individuals – the discoveries they make in the innovative efforts of laying out enlightened scientific principles, methods, ideas, and philosophies – remain poor and unappreciated during their lifetime. The selfish capitalist societies, however do not hesitate to profit from their discoveries at a later time. The observation further indicates that in smaller economies, industrialization may struggle to take-off because in such economies it is difficult to ensure immediate return of investments; or even in large economies where conditions are too stringent to function smoothly. However nowadays, governmental grants, guarantees, tax-incentives and bailout promise are attracting private capitals to venture in (one such area being the gov-private partnership). It is not difficult to see that the burden of all these gov initiatives falls ultimately on the shoulders of general public – with the gov levying taxes and gradually impoverishing people to make gov-private capitals fat and successful. In a capitalist system power is bestowed upon the owner of material wealth (money, to be exact) – and everyone else is a labor – irrespective of who they claim to be – whether white or blue color (although top white-color executives are treated as an associate and shareholder, while the lower white colors and blue-colors remain voiceless servants). Everything else – the immaterial wealth (such as happiness, see Happiness), is considered unimportant and therefore is taken out of the equation, or takes back seat. In such societies, the governing seats of power must withhold and promote the proliferation of private capital by assisting to find new markets for industrial goods and services. While such actions are incumbent upon the gov to assure the security of capital growth and flow – it does not and is reluctant to take any initiative or responsibility to assure job security to the labor force. However, the movement for organized labor force has paved a way - and Labor Unions are allowed in most countries. But, the capitalist outfit has its hand on it as well by imposing legal restrictions - in the manners of who and where such unions can be organized. Thus, another asymmetric system is imposed to allow a small fraction of the labor force the privilege of collective bargain power - while most are left out of the loop. Here, the rules of business take precedence over principles (as Dr BR Ambedkar, 1891-1956, outlined it, see The Mahatma – a Tribute). Further, to hide wealth distribution among the people it serves – the gov defines measures of social progress in terms of total money worth such as GDP. With the assurance of such gov supports – while many materialistic progresses were achieved – the capitalist system also ushered-in fierce and ruthless aggressiveness and corrupt practices – unleashing the greedy rush to acquire material wealth – within its borders and in transborder activities. In such rush, terms like winners and losers – are used to view everyone and everything to worship the winners and hate the losers – making the society highly confrontational, conspiratorial and conflict-ridden. The power of such social attitude is that, those who are called losers – sadly believe that they are really losers – thus inflicting scars of depression, worthlessness and hopelessness upon themselves. Further – there are constant temptations in capitalist entities to compromise quality of products and services, and fairness – unless enforcement of consensus based Standards, Codes and Manuals is in place. . . . 2. Capitalist Propaganda Adam Smith (considered the father of modern capitalist economy) asks that the adopter and proponent of the immediate profit-making capitalist system – must shelve the ideal of benevolence and fellow-feeling from their vocabulary. Further, they must use the tools of communication to convince the populace – about the merit and necessity of the system. His definition applied in industrialization endeavors reduced people into labor force and consumers – other aspirations, needs and wishes of people have secondary or no place in it. And, the tools of communication his theory implies – as one can understand, are the education-system, media, industry sponsored advertisements, political processes, elitist schools and intellectual accomplices or lackeys – all impregnated with the subtle flavors of propaganda in favor of capitalism. Even beliefs associated with philosophies and religions are used as a tool to promote capitalist system. The system, therefore says that people must become consumers - not only of capitalist products and services as livelihood necessity dictates - but also of information campaign. As an example, if one sees for long – the various programs in the mainstream media that accompany plethora of advertisements – one is likely to be totally brainwashed to the extent of believing that – media, politicians, consuming, and the powerful people of positions and wealth are the only things that matter in life and in social living (see leadership quality people want to see in Leadership and Management) – nothing else – people, values, nothing whatsoever matters. Thus, the capitalist power is dictatorial – having its hands on the string to control the behavior of people and whatever the system of gov is. Corruption, coercion and the deliberate promotion and sustenance of utter social asymmetry – are the rules of business within the capitalist power circles. In these rules, power and wealth connections take precedence over competence. Perhaps one can have a glimpse of it from the fact that – a person’s character is influenced by the company he or she keeps. One sad aspect of it is that – with the advent of TV technology in people’s daily lives – some got accustomed to learn certain things from what are broadcast on TV – getting highly influenced by the contents and polished advertisements placed by corporate entities, political parties, government and others. Not to speak of media (news, views and entertainment) in manipulation of information – so much so that such entities want people to know what they want them to know. These wealthy Shepherd direction setters – often targeting young people more than any other age group – take full advantage of this human psychology – to veer things to their liking – to turn people into nothing more than a Docile Lamb. With the dawn of internet age – another similar but more aggressive dimension has been added to this process. The power of effective communication (so much so that some words like socialism and communism have become hated terms in some countries) is such that – the fall-out from this mechanistic force became clear only in the late 20th and early 21st centuries. Destruction and degradation of Nature, Environment and Wild Life are only some of the fall-outs (see more in Warming Climate and Entropy; The Sanctity of Nature’s Wonders). The capitalist force required markets for its products and services, and raw-materials and slave labors as the means of production and for its sustenance. This gave birth to forceful colonization, eradication and destruction of native culture of countries in Asia, Africa and Americas – with the colonists forcing their own belief-system upon the colonial peoples. The colonists used them as sacrificial goats to build their prosperity and wealth. . . . 3. What Science Says Adam Smith was emboldened by R Descartes (1596 – 1650) Res Extensa or matter philosophy – that ignored and did not see the importance of Res Cogitans or human mind (see more in The Power of Mind; Symmetry, Stability and Harmony; the All-embracing Power of Sublimities) in everything a society needs to do for the benefit of mankind. Descartes philosophy – and its remnants continuing to govern social thinking today – in turn relied upon the developments of classical science (17th - 19th century). This period of deterministic science is basically defined by the foundation laid down by Galileo (1564 – 1642) and Newton (1642 – 1727). The period of modern science (20th century -) began with the pioneering 20th century science based on Relativity (see Einstein’s Unruly Hair), Quantum Mechanics and Uncertainty (see The Quantum World). It directs one to see the effects of mind – the observer-observed or subject-object relationship – in scientific findings. Although it is accepted by scientific community – the greater industrialization and management processes are far from accepting and linking the matter with the immatter. One can only hope that things will change and that Adam Smith’s economic theory and industrialization processes will be reformulated for the greater benefit of mankind. In around the same time, the principle of Laissez- Faire took root in France – saying to let the downstream condition determine what the upstream must do (or the supply-demand-chain as it is commonly known) – the principle became very popular and got widely accepted across the board. It laid down the foundation of competition and free-market-economy. But time and again, the upstream-downstream flow has been interrupted by sanctions and counter-sanctions – with adverse consequences that affected all – in particular, the general public. No wonder, some political thinkers saw the limitations of modern capitalist system. It is worthwhile to highlight what Sun Yet-sen (1866 – 1925), the Chinese Statesman wrote on the danger of industrialization based solely on capitalist economic system: Because of poverty, we must adopt the capitalist means of production to develop our resources to get rich. However, if we ignore the issue of social justice at the beginning of industrialization, we will sow the seeds of class warfare in the future. It is somewhat similar to a remarkable saying of Dr. BR Ambedkar on social contradictions (see Hold it There). In the 77th story (see the Revisiting the Jataka Morals-2) of the Jataka tales, the Buddha (see The Tathagata) tells a story about what could happen to a country when unwholesomeness and greed take control of a society. Unstoppable forward march of mechanical civilization! But sometimes it comes with a heavy price. Often there surface complains about some disturbing elements of unscrupulous industrialization push – the corruption associated with it are becoming more apparent in developing economies – but undeniably happened in every developed economy during the take-off, and even in modern times. First, when policies and laws are enacted without consultation and utter disregard to the interests and concerns of people deemed to be affected by the push. Such negligence amounts to reducing the impacted peoples – to nothing but a disposable sheet of paper. The second occurs during the implementation phase of industrialization checklist procedures – for example, in cases where land acquisition is required at the cost of dislocating people and their livelihood. Among many unreported incidents – oftentimes there surfaces allegation of highhandedness on the part of administering bureaucrats and political hooligans – who do not hesitate to harass hardworking people by threatening and intimidating them. The purpose is to deprive them of any compensation money. The tactic often comes with additional forces to collect bribes and pocket the money – and to stop complaints of any sort. . . . 4. The Grammar Intro With this brief note (brief, but ended up somewhat longer than I intended) outline – that gives one a necessary background for understanding the industrialization processes, it’s time to get into the topic. I have developed the shown image indicating the Standards, Codes and Manuals as the grammar and best-practice guidelines for the success of industrialization. All three – come under the disclaimer envelope where the authors and publishers of them disclaim any legal responsibility if something goes wrong with their application. The disclaimer is necessary because it is impossible for the expert authors to visualize each and every possible cases and situations of applications. For example, the British Standard BS 6349-1:2000 (Maritime Structures) says: Compliance with a British Standard does not of itself confer immunity from legal obligations. Despite such disclaimers, if there is some sort of failure using a certain standard – the reputation of that standard is tarnished. Among the three, Standards and Codes come under the purview of certification and regulatory envelope – which means they are mostly authorized by regulatory entities in their jurisdiction to be applied as a minimum to ensure best practices – and can be referred to in legal cases (subject to the disclaimer warranties claimed by them). The manuals, on the other hand are cook-books based on Standards and Codes, and on established research findings up to the time of their writing – and are designed as a step-by-step procedure for doing something. . . . 4.1 Engineering Profession There is another regulatory hand that is used for controlling the practice of professional engineers. Similar to law and medical professionals, the regulation exercised by state/provincial govs within their respective jurisdictions – requires an engineer to hold a license to practice. There are few points to be made in this regard: First, it is often accused of having adverse effects by inhibiting the free mobility of engineers from one state to another – as the modality of reciprocity or comity is not widely established. Second, this system of engineering licenses does not have wide acceptance, and is not practiced by many countries in the world. The rationale for such a stand is that degree from an accredited university, length of experience, prevalent social morals and ethics, and national laws – are considered adequate to ensure quality and holding an engineer accountable. Further, they emphasize on registration and licensing of engineering firms and entities rather than individuals – and consider individual licensing system as another layer of jurisdictional hurdle. Third, multinational corporations also pay less importance to such jurisdictional hurdle in their capacity to utilize manpower stationed in different countries or in outsourcing – but ultimately, they are required to comply with the regulations in countries where they exist – by getting the final product reviewed and signed by a licensed professional – the Engineer of Record. But this practice, has a drawback in it – because a signing engineer is supposed to remain involved throughout the process of planning and design – at least in supervisory capacity. Last but not the least, many engineering decisions are made by powerful unlicensed non-technical people in an org – their influence and decisions have many ramifications on the soundness of an engineering project. How engineering licensing is helpful in this regard? Here are something relevant – in the 1955 Grinter (Prof. Linton E Grinter, then Graduate Dean of the University of Florida) Report, Summary of the Report on Evaluation of Engineering Education, published in the 1994 January edition of the Journal of Engineering Education ASEE Link. In section on III.B. Assimilating New Scientific Material, it writes: . . . there is a great deal of similarity, both in conceptual understanding and in analytical methods, among the generalizations of heat flow, mechanics of fluids, electromagnetic fields, and vibration theory. When a student understands these generalizations, he has gained a concept of systematic orderliness in many fields of science and engineering; he is therefore able to approach the solution of problems in widely diverse fields, using the same analytical methods. This unification of methods of analysis can be accomplished to a considerable degree without reaching beyond undergraduate mathematical levels . . . In section on III.G. Engineering Analysis and Design: . . . The capacity to design includes more than mere technical competence. It involves a willingness to attack a situation never seen or studied before and for which data are often incomplete; it also includes an acceptance of full responsibility for solving the problem on a professional basis. . . and creative thought and imagination are brought to bear in producing an integrated system. To do this is a difficult and challenging job, but a very necessary one. . . In, Setting the Standards for Engineering Education: A History, Proceedings of the IEEE | Vol. 105, No. 9, September 2017 (NSF), author Atsushi Akera wrote . . . the Grinter Report. . . recommended a bifurcated system of accreditation along “professional-scientific” and “professional-general” lines . . . With this, let us move forward. This is the 77th piece in the WIDECANVAS (see links to all the posted essays in the Website Links and Profile). . . . 5. Industrialization In simple terms, industrialization refers to the utilization of technology and machines for mass manufacturing of a product – with the machine-driven customization of processes that lay importance on smoothness of work-flow, efficiency and cost-minimization. The customization includes starting with the procurement of raw materials, and ends at marketing the finished products. Although the processes started with manufacturing – the same principle now governs all economic sectors including services sector and gov businesses. To ensure smooth and timely operation of these processes – acceptable standards of measure, definitions and specifications of things – the consensus-based best practices guidelines have become necessary – as a grammar that can be safely applied routinely across the board in specific areas of operation. The predecessor to such industrialization was hand-tool customization – and its envelope included many earliest standardization efforts that shaped social cohabitation, trade and commerce. During that time – economic activities were more of a family affair in the form small businesses where the relation between employer and employee was one of sustainable cooperation and complementarity. Industrialization, riding on the capitalist bandwagon, while contributed to the development and accumulation of material wealth – destroyed that kind of relationship, making things highly mechanistic – turning it into hour-to-hour counting of works vis-à-vis wages. Modern societies are waking up to realize that – such a mechanistic relationship is unsustainable – and is responsible for many social ills and negative stresses – that are ultimately affecting the productivity and interests of the labor force. While the mechanistic relationship administered through checklist procedures is forced upon the populace - exclusive luxurious clubs for the wealthy and powerful define the relationships of these privileged classes - the Shepherd Club, where decision processes and strategies are formulated - in secrecy and confidentiality - to govern the general public. This implies that emerging developing economies must exercise due diligence – to filter out what to accept and what to reject during the processes of industrialization. Because a carbon copy adoption of developed-economy methods – without learning from their mistakes – may give birth to the same social ills they have been facing. History shows that a smart adaptation of foreign ideas and methods yields the best benefit – given that a society is heedful to their own cultural values, traditions and strengths. The industrial revolution that started in the 18th century United Kingdom and United States of America – needed the customization of the industrial processes to achieve the full force of mass production – stressing on efficiency and lower cost of production. The science and technological development needed for starting this revolution – were provided by some remarkable discoveries and inventions which, among others included James Watt’s (1736 – 1819) steam engine invention; NLS Carnot’s (1796 – 1832) thermodynamic theory; and the technological transformation of textile industries from handlooms to machine-driven factories. Industrialization successes needed standardization of processes to create products and services – in virtually every sectors of economic activity. Although standardization processes started in pre-industrial agrarian societies in accordance with the technological advances during that time – industrialization gave urgency, new meaning and importance to it – otherwise increased economic activities will be hindered by chaos, confusion and conflict of interests. They are the necessary grammar and best-practices guidelines required for the growth and proliferation of industrialization – capitalist or non-capitalist. Based on the basic understandings described in these paragraphs – let us focus on engineering or applied science aspects – by narrowing down the topic to civil engineering contexts – but looking through coastal engineering perspectives, in particular. The focus is described in two headings – Standards and Codes, and Manuals. The first of these industrialization grammatical materials are administered, authored and published by bureaucratic-technocratic organizations that thrive on gov grants/finances, participant membership/subscriptions and any other contributions. Even some manuals fall into this category. These orgs work under the umbrella of non-profit entities. With this umbrella over their head, they can take tax advantages, and can ask for donations, contributions and volunteer hours from the members of general public. The irony is that pay packages, benefits and privileges of executives of such orgs (same is the case with tax-payer funded UN organizations; for that matter with Charity Organizations and Political Parties) – even their travel habit in first and business classes – surprises the hard-working donating public who cannot even afford to travel in economy class. The reality is that such orgs are in the business of profit making – of different sort – and that is the reason why so many of them exist. Further, the trend nowadays is that many are in the business of giving certificates and awards – thus attempting to raise themselves to the rank of an undeclared authority. This practice essentially denies the relevance of education, experience and expertise – which have always been an asset for an individual – and for the entities he or she serves. The materials they produce are not freely available – although outdated digital versions are often offered free of cost to the public. Manuals are authored by expert scientists and engineers of research institutions, industry experts as well as by standard organizations. The prime examples are the Shore Protection Manual and Coastal Engineering Manual of CERC (Coastal Engineering Research Center) – an organization owned and run by United States Army Corps of Engineers (USACE). US federal gov made it mandatory that all manuals funded by it, their digital versions – must be made freely available to the general public. . . . 6. Engineering Standards and Codes The earliest standardization in human history was developed within the envelope of hand-tool customization – by starting with the standards for measuring length and mass (in customary terms weight is used instead of mass, but weight is the downward gravitational force exerted by a mass). Use of forearm and finger as the measures of lengths, and different sizes of stones as the measure of mass were perhaps the earliest of such efforts (see more in Turning the Wheel of Progress). As the societies began to take shape, the counting system, speaking and writing grammars, and the metallic coins appeared to help people communicate and doing trades and commerce. And each culture developed their own unique system – which saw the continuation of amalgamation – as means of travel improved with domestication of horses and invention of wheels and wheeled-carts. Cottage industries of various sorts – pottery, textile, mining, metallurgy, etc – began with agriculture and domestication of plants and animals. At the same time philosophical and religious moral standards started taking root to establish social order. Before moving further, it is helpful to add a few more sentences on the history of System International or SI that has been adopted as a common measure of units across the globe. It replaced earlier arbitrary customary units of different localities and states – that gave rise to the differences in definitions and interpretation – to confusions and conflicts. Britain as the colonial superpower introduced its system – later called the FPS unit system – with the unit of a Foot for length, Pound for mass and Second for time. The colonist promoted the system wherever it set foot in. FPS is an arbitrary unit system lacking scientific reasoning (even the unit of currency is called Pound). Therefore, the need for a common advanced standard system was felt – and the European Renaissance (~ 14 to 17th century) gave that opportunity. The gov in France took the initiative by giving the task to the Academie des Sciences – which appointed five prominent scientists of that time to define a common standard. Thus the metric decimal SI system – as a rational and systematic unit of measure was born and accepted in 1791. Decrees promulgated by French President Napoleon Bonaparte (1769 – 1821) – made it imperative that all European countries (except United Kingdom) adopt the system. It soon became very popular – and is now a global unit of measure. But, USA, the leading superpower in the world – remained ambiguous. The National Bureau of Standards, in its Miscellaneous Publication 286, 1967, Units of Weight and Measure – International (Metric) and U.S. Customary wrote: Henceforth it shall be the policy. . . to use the units of International System (SI) as adopted in the General Conference on Weights and Measure (October 1960), except when the use of these units obviously impair communication . . . Unlike every other countries in the world (including Britain that adopted it in 1988), this exceptional clause in the declaration prevented blanket adoption of SI system in the US. While the US scientific communities switched to the SI system – media, engineering and every other sphere of activities – continue to use both – often in favor of the customary British unit. Before moving further, a distinction has to be made between model standard and standard, and between model code and code. The difference is clarified by International Building Code (IBC). It defines a model code as: A model code is developed by a standards organization, typically using the voluntary consensus standard processes and subject matter experts. The intent of a model code is to have an industry-wide standard that can be adopted and customized by local jurisdictions, thereby saving the jurisdiction the time and expense of developing and maintaining their own code. A model code is not enforceable until it is adopted by a jurisdiction. Because of review and modification processes before a model code can be adopted by a jurisdiction, a code generally lacks behind a model code in time. The same logic applies for standard and model standard. STANDARDS: Now let us clarify our understanding of the definitions of Standards and Codes and the differences between the two. NIST (National Institute of Standards and Technology) A-119 details out the definition of Standards: the definition of terms; classification of components; delineation of procedures; specification of dimensions, materials, performance, designs, or operations; measurement of quality and quantity in describing materials, processes, products, systems, services, or practices; test methods and sampling procedures; or descriptions of fit and measurements of size and strength. In other words, a Standard consists of technical definitions, procedures and guidelines that specify minimum requirements or instructions for creating products and services. It provides a common reference for engineers, manufacturers and bidders. Among the thousands of Standards, the voluntary consensus standards are the most familiar ones with engineers. According to NIST, these standards are developed in a manner that is open, considering balance of interest, with due and appeal processes, relying on consensus meaning general agreement rather than unanimity. CODES: Again referring to NIST: A code is a standard that has been enacted into law by a local, regional, or national authority in their jurisdictions so that engineers and contractors are legally obligated to comply with the code. Noncompliance can result in being prosecuted. Codes are laws and regulations that have their eyes on ensuring public safety and health. Technical Regulation is a mandatory government requirement that defines the characteristics and/or performance of a product, service or process. As a further distinction between the two: a standard is detailed in nature – in its scientific content and justifications of those contents – most often with minimum or no input from law professionals. A code, on the other hand can afford to be less detailed because it relies upon and makes references to the relevant standards. Codes come under detailed scrutiny exercised by law professionals. This is because, once enacted into a law by a certain jurisdiction – codes have legal ramifications, although the liability lies with the applicators – the contractors – builders and consultants. As described before, Standards and Codes usually come up with some form of specifications. A specification is a set of conditions and requirements of precise and limited application describing details of a procedure, process, material, product or service for use primarily in procurement and manufacturing. Here is a list of some Standard Organizations of some major countries. They are all members of the International Standard Organization (ISO) and works in coordination with it – to adapt ISO standards to local conditions and elements – to ratify them to regulatory Codes. It was founded in 1947 in Geneva, Switzerland as a non-governmental organization to bring together experts to share knowledge and develop voluntary, consensus based, market relevant International Standards. By 2017, it has some 163 country-representing members. American National Standard Institute (ANSI) – is a voluntary consensus based standard institution, which took its present name in 1918 from its predecessor American Engineering Standards Committee (AESC). Its establishment has been initiated in 1916 by American engineering societies together with ASTM (American Society for Testing and Materials). The participants in this organization include gov agencies, educational and research institutions, industry experts and trade associations, and interested individuals. Many industries around the world use ANSI specifications – while rolling out their products. The National Institute of Standards and Technology (NIST) – is a US federal gov institute under the US Department of Commerce. It was established in 1901 to enhance competitiveness of US industries against its rivals from other countries. The Standardization Administration of China (SAC) is the Chinese Standards Organization instituted by the State Council of China. It came into effect in 2001. GOST is a Russian Standards Organization that came into affect in 1968 – is now administered and maintained by Euro-Asian Council for Standardization, Metrology and Certification (EASC). It works under the umbrella of the Commonwealth of Independent States (CIS). The Bureau of Indian Standards (BIS) – was established by an Act in 2016 and came into effect the following year. It reincarnated from the earlier Indian Standards Institution (ISI) that was established shortly after India’s independence. In accordance with other major British colonies like Canada, Australia, New-Zealand, and USA – Indian Standards were highly dependent on British Standards (BS). The divergence away from this colonial legacy is gradually being updated. The Japanese Industrial Standards Committee (JISC) is the Japan’s National Standardization Organization. Canadian Standards Association (CSA) – now working under the umbrella of CSA Group was launched in 1919. Standards Council of Canada (SCC) – a federal gov institution, accredited CSA to develop standards in the spirit of voluntary participation of industries and individuals. Within the political union, EU – EUROCODES was initiated to formulate a common standardization of different European country-standards that existed in member countries. It came into effect in 2010. Under its umbrella are some major institutions such as: The French Standardization Association known as the Association Francaise de Normalisation (AFNOR). Based in Paris it is the countries organization that administers other sister organizations and coordinates with International bodies like ISO. Similar like AFNOR, German Institute for Standardization (DIN) is the German Standard Organization that works in coordination with ISO. British Standard (BS) has some of the robust codes in the world. It fundamentally formed the basis of standards of many post WW II colonies and countries. BS merged within the framework of EUROCODES after it joined EU. The post BREXIT period starting in 2020 – may see BS re-emerging in the changed perspective. API – American Petroleum Institute through its Standards Department is entrusted to develop standards and manuals catering to the needs for planning and design of offshore platforms for oil and gas industry. ASCE – American Society of Civil Engineers through its Structural Engineering Institute (SEI) is entrusted to define minimum design loads in areas of wind and other forces. The latest SEI 7-16 was issued in 2016. IALA (The International Association of Marine Aids to Navigation and Lighthouse Authorities, also known by its French name AISM (Association Internationale de Signalisation Maritime) is a non-profit organization responsible for harmonizing standards and codes on maritime navigation and navigation aids. . . . 7. Coastal Engineering Manuals As outlined earlier, manuals are primarily written as a cook-book – that are based on Standards and Codes, and on established research findings up to the time of their writing – and are designed as a step-by-step procedure for doing something. They are specific to certain products or methods – and accompany them while released for market consumption. They are not mandatory, but are meant to be followed for whom they are primarily issued. Some coastal manuals are not freely available to practicing engineers although the responsible organizations are dependent somehow on tax-payer funding and member subscriptions. Exceptions are USACE Coastal Engineering Manual, US DOT, EUROTOP, Rock Manual, NAVFAC – US Navy, FEMA, UNCTAD and WMO. Here is a brief list of some institutes that author and publish manuals in their respective areas of activities. As briefly outlined before, United States Corps of Engineers (USACE) through its Coastal Engineering Research Center (CERC) is entrusted to and has issued extensive sets of coastal engineering manuals (CEM) that worked as a reference material for many standards and codes. These manuals replaced USACE 1984 Shore Protection Manual (SPM). US Department of Transportation – US DOT through its National Highway Institute (NHI) of Federal Highway Administration (FHA) is entrusted to develop practical guidelines for Highways and Bridges. DNV (Det Norske Veritas) is a Norwegian organization is entrusted to develop planning and design codes and manuals of offshore structures. EUROTOP has been developed primarily by Dutch Institutions TAW (Technical Advisory Committee) on Flood Defence, the Netherlands and H.R. Wallingford, UK. The EUROTOP manuals provide a thorough treatment of wave overtopping of coastal and maritime structures. It forms part of EUROCODES. US Navy Department of Defense (DOD) is entrusted to develop Unified Facilities Criteria (UFC), which replaced many earlier US Navy standards known as NAVFAC manuals. OCIMF or Oil Companies International Marine Forum is an industry-sponsored standard guideline to facilitate design of mooring of oil and gas tankers. PIANC – the Permanent International Association of Navigation Congresses based in Brussels has been the source of guidelines for maritime engineering for many decades. Founded in 1885, the organization has been renamed as International Navigation Association afterward. More recently, it has been renamed again as The World Association of Waterborne Transport Infrastructure. It has three technical commissions: Inland Waterways and Ports (INCOM), Maritime Navigation Commission (MARCOM) and Environmental Commission (ENVICOM). PROVERBS – the Probabilistic design tools for Vertical Breakwaters is a European Commission funded project entrusted to develop probabilistic design tools for vertical Breakwaters. The institute has developed some cutting edge materials on probabilistic design concepts for coastal and maritime structures. Rock Manuals are published as part of EUROCODES – primarily by UK based CIRIA (Construction Industry Research and Information Association), the Netherlands based CUR (Civil Engineering Research and Codes of Rijkswaterstaat) and the France based CETMEF (Centre d’Etudes Techniques Maritimes Et Fluviales). Since published in 2007, the manual has become very popular among coastal engineering professionals. FEMA or Federal Emergency Management Agency has some very good guidelines and resources dubbed as Coastal Construction Manual. United Nations Organizations like WMO (World Meteorological Organization) and UNCTAD (United Nations Conference on Trade and Development) have some recommended guidelines for port developments in member countries; and IPCC (Intergovernmental Panel on Climate Change) findings and recommendations. Others include: SIGTTO (Society of International Gas Tanker and Terminal Operators Ltd); SOLAS(Safety Of Life At Sea); Coast Guard organizations of different countries such USCG (United States Coast Guard) and CCG (Canadian Coast Guard); UK Department for Environment for Flood Control and Coastal Erosion Risk Management or DEFRA; United States Institute for Water Resources (IWR), National Economic Development (NED). . . . 8. Some Concluding Remarks As a summary let me highlight the following: Each country, state and large corporations develop their own policy of compliance with one or more specific standards and codes – they ratify. Country and state policies so outlined become legal regulatory code. This is necessary because it is time consuming and impossible for each contractor and builder – to consult every existing standards, despite efforts of harmonization. Standards, codes and manuals usually lag behind the advances in research in science and engineering. These documents are what is commonly known as the customized ‘one-size-fits-all’ cook-book type publications. Apart from codes that mandate a regulatory minimum compliance – one needs to tailor them by examining their scientific and technological soundness, adequacy to requirements, etc – all these depending on the nature and type of a certain problem or case. Therefore – the applicators need to look for materials beyond the customized materials – this is especially true for non-routine applications. The articles Uncertainty and Risk and The World of Numbers and Chances – provide some good insights on this matter. Thirdly, pointing to finger to disclaimer – it can be explained further that the authors of standards, codes and manuals – are not involved or privy to many details of a particular project. Therefore, it is the responsibility of practicing engineers and the organizations they represent to ensure safe and sound designs. It implies that wherever deficiencies in such materials become clear – they should be brought to notice. A legal battle often tarnishes the image of a company and does irreparable damages to its reputation no matter how one can blame on standards, codes or manuals. Compliance with environmental, wildlife protections – and conservation of Nature and the interests of indigenous communities – and the effects of engineering interventions on them – cannot be relied upon the entirety of standards, codes and manuals. Because these areas of engineering works – are rather fluid as new information and assessments are continually coming to light (see more in Warming Climate and Entropy; Sea Level Rise – the Science; Sea Level Rise – theConsequences and Adaptation; Environmental Controls and Functions of a River). Therefore due diligence on these matters lies upon the shoulder of the practicing engineer. Finally, it is important to highlight one more time that smooth and sound progresses of industrialization can only proceed when standards, codes and manuals are thoroughly researched – and the enforcement of them is well-established. To do that effectively – highly skilled and knowledgeable work force is imperative – which means that facilitation of the availability of mere capital is not enough. It is worthwhile to note here that inconsistency of Standards has been mentioned as one of the causes of the 2017 Grenfell Tower Inferno, London England. In conclusion, it is important to realize that a practicing engineer cannot and should not adopt blind compliance with standards, codes and manuals – to assume that their designed structures are unambiguously safe and sound. It entails therefore, that while working to implement and install something in the real world – any encounter with unreasonable and unscientific findings should be brought to notice. Also, it is important to state here that – an engineer is expected to be cognizant of science or physics behind the materials covered in manuals, standards and codes. Otherwise, his or her services will render to something no more than a mechanistic application or a technician’s job. . . . There we have it. This essay is perhaps the longest one in WIDECANVAS. The topic is a very interesting one – and there are lots of grounds to be made. In the end, it is worth the effort – to clarify some of the things that are often not thorough enough – both in contents and contexts of descriptions, definitions and interpretations. I have started this topic quite a while ago – and happy that I was able to post it finally. In honor and celebration, it is posted on the eve of Bangladesh Independence Day - the 26th day of March in 1971. Before finishing, let me quote a few lines from U Thant (1909 – 1974) who had a decade long tenure as the UN Secretary General (1961 – 1971): Every human being of whatever origin, of whatever station, deserves respect. We must each respect others even as we respect ourselves . . . Wars begin in the minds of men, and in those minds, love and compassion would have built the defenses of peace. . . . The Koans of this piece: Sorry, you can only look but cannot go backward, because the wheel of TIME has forgotten to fit the rear gear on . . . Build, nourish and protect your own reputation—because it cannot be bought in the market with fair means . . . Why heading to hell when the heaven is next door. . . . . . - by Dr. Dilip K. Barua, 25 March 2023  . . . the trouble with the world is that the stupid are cocksure and the intelligent are full of doubts. . . This saying from Bertrand Russell (1872 – 1970) is similar to what The Tathagata said in the 152nd verse of the Dhammapada: The man of little learning grows old like a bull. He grows only in bulk, but, his wisdom does not grow. These sayings point one to look deep into things to open one’s wisdom eye, to see the reality of the nature of things – of the existence of uncertainty in the sphere of knowledge (see The Quantum World; Uncertainty and Risk and The World of Numbers and Chances). The necessity of seeing as such – dawns as we continue to learn more – as the horizon of our knowledge continues to expand.
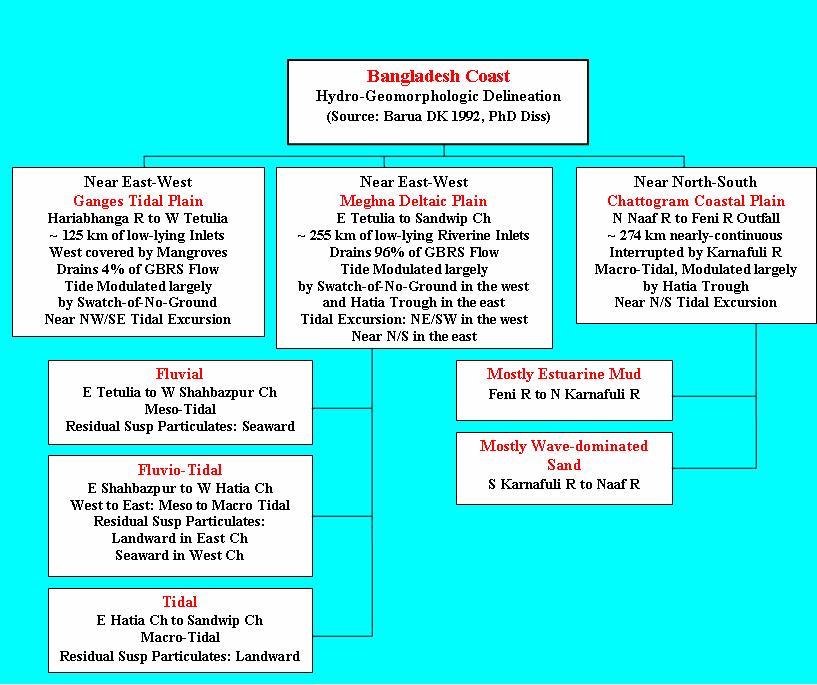
Perhaps – our learning process starts as we begin to develop questions in our mind – like if or when. In computer programming ifs and the answers to such ifs – are used to direct processes in different directions – so does our learning processes. Questions similar like these, reflecting on the past: if I had done things differently . . . if I had been informed differently or were able to see things through my own lens . . . if I had someone powerful on my back . . . so on – and so forth. And intelligent answers to them help us chart future directions. Similarly, such questions can be framed in our mind – at any time – to help examining the pros and cons of making decisions. Sometimes, we fail to ask such questions in time, and mistakes are made – from which recovery becomes difficult. It’s like one of Tagore (1861 – 1941) songs: keno jaminee naa jheta jagelaa naa – saying, why didn’t you wake me up before it was dawn. In one way or another – the consequences of making decisions based on answering ifs –– define the interdependent fluxes in the evolving canvas of life in time, and in the space where one lives – the spacetime. And as we do so, we begin to realize what Benjamin Franklin (1706 – 1790) once said: . . . without continual growth and progress, such words as improvement, achievement, and success have no meaning . . . Starting from these words of wisdom, let us attempt to understand some dynamics of currents in coastal oceans off rivermouths – focusing on the one, off the mouth of Ganges (Ganga) Brahmaputra River System (GBRS; or the GBM system). Needless to say that such understandings – are very imperative to initiate, manage and execute Civil Engineering on Our Seashore – to achieve sound and sustainable goals. Engineering services are involved in one way or another – in the processes of attaining the 17 interconnected UN declared Sustainable Development Goals (SDG). . . . 1. Coastal Currents Intro Thought of presenting some findings from the 2nd Chapter of my Ph.D. Dissertation – with a note that unlike in An Alluvial River’s Sedimentary Functions, I am keeping the name Brahmaputra River in line with my Dissertation – although its reach in Bangladesh is known as the Jamuna River. Some aspects of this chapter were presented in the Characterizing Wave Asymmetry, with discussions of some theoretical frameworks posted in Nonlinear Waves. This is the only chapter – which I could not manage time to send the manuscript for journal publication. Other chapters are published: Chap 1 (1991), Chap 3 (1995) and Chap 4 (1994). Facilitated by my major Prof WS Moore, the 2nd Chapter benefited from the works and advice of my Dissertation committee member Prof B Kjerfve. Acknowledging them in gratitude – let me move forward to focus on the main contents of this piece – on coastal ocean currents. In this essay, I am doing this very briefly with some of the interpretations and explanations that accrued from my later experiences and related publications – some of which are summarized and listed in the ABOUT page. Among them, the most relevant publications for this article are: the 1990 IEB Journal Paper on Estuary; the 1991 COPEDEC-PIANC paper; the 1993 Practices and Possibilities; the 1994 Karnafuli River Estuary Hydraulic Behavior; the 1997 Active Delta; the 2001 Suspended Sediment Measurement; the 2002 Geometric Similarity of Deltas; the 2004 Settling Velocity of Natural Sediments; the 2008 Fluid Mud; the 2015 Longshore Transport; and the 2017 Seabed Roughness. It is also enriched by the works done while writing several articles posted in the WIDECANVAS. Before I begin, a short note on The Coastal Force Fields is helpful. The fields represent a playground of many forcings and responses of different time-scales afforded by different constraints – defined by isobaths and the land-water interface at the shoreline/coastline (see more in the Civil Engineering on our Seashore). Together, the system of forces head to reach dynamic equilibrium (see Natural Equilibrium; Water Modeling). According to the force fields defined there – GBRS mouth is governed by forces – that are in dominant actions, but differing in the contexts of both space and time - the Metocean Force Field (MOFF), the Extraterrestrial Force Field (ETFF), the Land Drainage Force Field (LDFF) – are all there, together with the Frontal Wave Force Field (FWFF) – which is active in the proximal shoreline and shallow areas. As well important is the Storm Surge that frequents the coastline often. Currents or velocity fields are generated by the development of pressure gradients generated by the highlighted force fields. They are a manifestation of hydrodynamic interactions – of force and response fields – as depicted in the image of Force Fields in a Coastal System. . . . 2. The Hydro-Geomorphologic Setting – the Processes and Forms. Let me begin by referring to the attached image (it is enriched by some materials discussed in the Coastal River Delta) – that summarizes some of the key hydro-geomorphologic features and processes of Bangladesh coast. The definitions and delineations have been used by many subsequent authors to describe Bangladesh coastline. The delineation identifies two major groups – the first is the (~) 380-km near-east-west delta of the GBRS, and the second is the (~) 274-km near north-south stretch of the Chattogram coastal region – the Chattogram Coastal Plain (CCP). Following the terms defined in the Force Fields in a Coastal System, the hydrodynamics of these two groups are fundamentally different – with the regular playground of spring-neap ETFF – more so in the eastern channels than in the west. The delta is the showcase of interacting LDFF and MOFF during the four months of the wet-monsoon – roughly from June to September. While the dominance of LDFF is present close to the shore delta fringes – the MOFF dominance is in contagious seas offshore. In the second group CPP – on the other end, MOFF is the dominant process riding on top of ETFF. The first group can be divided into two: the (~) 125-km long coastline of the Ganges Tidal Plain (GTP) in the west, and the (~) 255-km long coastline of the Meghna Deltaic Plain (MDP) in the east. Of these, the first draws only 4% of the GBRS flow – with the delta fringes of multiple interlinked estuaries colonized by extensive mangrove forests – the Sundarbans that stretch from India to Bangladesh. As the name suggests, the GTP is mainly tidal with muddy estuarine channels fringed by narrow and pocket beaches of fine sands at the shoreline. The second draws the other 96% of the GBRS flow – and is the highly dynamic active delta of the GBRS. Horizontal coastal erosion rate to the maximum of 400 m/year, and the vertical sediment accumulation rate to the maximum of 3 m/year were observed (the 1997 paper). The delta is stratified horizontally (the 1990 paper) in current patterns and SST (suspended sediment transport; see the Hydraulics of Sediment Transport for definition) – with seaward residuals in western channels and landward in the east. With such trends of differing residual transport directions associated with stratification, the delta-building processes appear poised to prograde southwestward with gradual of shoaling of eastern channels. Two submarine canyons incise Bangladesh coastal ocean. The first is the Swatch-of-No-Ground (SNG) – or Ganges Canyon in the west (the SNG has a width of 30 km, at 200 m isobath, and penetrates 130 km deep into the continental shelf). A shallow trough – the Hatia Trough (HT) runs parallel and close to the CCP. As discussed further later, these two canyons modulate tidal phenomenon ETFF processes in the Bangladesh coastal ocean. . . . 3. The Measurements – the Time, Tide, Site and Season. Let me briefly outline the measurements on which the findings described in this article are based (please refer to Chapter 2 of my 1992 Dissertation for details). A total of three different sets of 13-hour time-series hourly observations cover several stations. Land Reclamation Project survey vessel, M.V. Anwesha was used for observations. A Decca navigation hyperbolic system was used for positioning. The vessel was let to weather-vane – positioned by a bow anchor (with an anchor-chain measuring 3 times the water depth). Velocity was measured by an Ott propeller current meter. A 50 s exposure time was used to obtain the flow velocity. The propellers were calibrated before the measuring campaign in the calibration tank of Bangladesh Water Development Board and were accurate within (+-)2%. With one current meter suspended from a davit located on the mid-section of the ship, measurements were made at three depths (1 m below surface, mid-depth and 1 m above bottom), either starting at the surface or at the bottom, and sampling the mid-depth position during hoisting or lowering. Depending on the depth, 8 to 10 minutes were required for the exercise. The velocity direction was measured by the ship's navigation compass and the deviation from it was noted by a pendulum current meter lowered simultaneously at the level of the current mater. A total 14 measurement sites were covered – in waters between 5 and 20 m isobaths. Of them, 4 are off the GTP – one at the head of SNG with 3 others on the west of it. Three sites are in locations parallel to CCP stretching from the head of HT to Sandwip Channel. The rest 7 measuring stations are located off MDP. The first set of measurements representing a spring tide – covers 5 stations from 27 November to 1 December 1989. Measurements at these stations were repeated the following week (5-9 December) during a neap tide. These sets of measurements during November-December represented GBRS slow falling stage. The second set of measurements representing a mean tide – covers 6 stations during a 22-26 August 1990 period. This set of measurements during August represented GBRS peak stage. On a 17-24 October 1990 period, a third set of measurements cover 6 stations. During this period, the first measurement on 17 October represented a spring tide, and the rest, a mean tide. This set of measurements during October represented rapid falling stage of the GBRS flows. A lone measurement on 15 March 1991 during a spring tide represented a flat low GBRS stage. Among these, the August 1990 measurements represented southwest monsoon while those in October, November-December was during the northeast monsoon. These two seasons represent contrasting wind speed magnitude and directions. Swells having 12-16 s periods were observed at a station, west of SNG during the October 1990 measurements. For a location in the Bay of Bengal near the SNG, sea and swell charts of the U.S. Navy (1965) indicate high seas and swells from southwest in August – moderate seas and swells from Southeast in October – and low or negligible seas and swells from northeast in November and December. . . . 4. Coastal Water and Wind-driven Circulation. Here is a gist on the nature of changing seawater salinity (see Coastal Water to know aspects of it) at measured stations, and the wind-driven circulation (see Storm Surge to know aspects of it). The depth-and time-mean (averaged over the semi-diurnal tidal cycle) salinities indicate the enormous influence of GBRS at the measured stations. At no station does the observed salinity exceed 50% of the full strength seawater salinity. Stations sampled in August 1990 during the peak river-discharge period were fresh or mildly brackish. As expected the seawater salinity off the MDP is substantially lower than those stations on both east and west sides – indicating a high influence of GBRS fresh water flow at these stations than others. All the measured stations show a vertically well-mixed situation. Time-mean salinities at 1 m below surface and at 1 m above bottom showed negligible variations over the depth. Absence of vertical density stratification indicates that no estuarine type circulation is present (see aspects of it in Managing Coastal Inlets). Countries bordering northern Indian Ocean experience oscillating monsoon wind systems. The southwest (June through September) and the northeast monsoons (December through February) cause the reversal of circulation in the Bay of Bengal. It can be noted that when wind blows for a long time (for a pendulum day, which is 65 hours for Bangladesh coast; Dissertation) against a coast, a drift current develops and a wind set-up is created at the coast. The wind set-up causes a slope current down the gradient. The drift current is a function of depth and due to frictional resistance at the bottom, is higher near the surface. The combination usually results in a net onshore surface drift current and a net offshore slope current along the bottom. . . . 5. Submarine Canyons Refract Tide. The set of measurements in waters between 5 and 20 m isobaths – covering nearly the whole stretch of Bangladesh coastal ocean indicate something very interesting about the refraction of tidal wave by deep submarine canyons. Measurements on the two sides of the SNG reveal that the tidal excursion directions are different on the two sides of the canyon. Most of the shelf areas surrounding the SNG receive tidal forcing from it. While a dominant northeast (rising)–southwest (falling) tidal excursion occurs on the east of SNG, the same on the west is northwest (rising)–southeastward (falling). This pattern, observed for the first time in my Dissertation works – indicates that tide propagating faster through the canyon than the surrounding shelf areas – refracts to either side The result is that the surrounding shelf areas receive tidal forcing generated from the canyon. It appears, however, that this refracting effect of SNG on the tidal motion does not cover the areas as far east to HT. The excursion pattern in stations near HT shows a nearly rectilinear tide propagating through it – and is oriented north-south. Analogous to the refraction of short waves by a submarine trough, a canyon causes divergence of tidal wave energies on both sides of it. The result is a higher amplitude tide on both sides than at its head. The agreement to this observation can be found in co-range tidal lines. Why the tidal waves propagating through SNG and HT are different? Answer to this question becomes apparent from the principles of long wave transformation outlined in the Tsunami and Tsunami Forces piece. On shoaling and funneling of long waves I have written: The phenomena of shoaling and funneling can best be understood by applying the energy conservation principle, often known as the Green’s Law. This simple principle assuming no losses of energy by friction, etc., shows that for a gradually shoaling continental shelf, the ratio of height increase is proportional to the reciprocal of the ratio of depth decrease raised to the 1/4th power. For a channel gradually decreasing in width, the funneling effect is given by the ratio of height increase that is proportional to the reciprocal of the ratio of width decrease raised to the 1/2nd power. In the case of tide propagating through the gradually varying configuration of HT, both the effects of shoaling and funneling are pronounced – resulting in amplification of tide continuing up to Sandwip and Hatia Channels with further effects there (the COPEDEC-PIANC paper). In the case of SNG – the canyon is so deep incised into the continental shelf that the propagating tidal wave virtually does not feel the Green’s Law effects until reaching the head of the canyon. But, there it faces the reflection from the steep canyon wall. The combined effects of loosing energy by reflection and refraction must be the primary reasons why the tidal ranges in areas around SNG are lower (lower than HT areas). However, once the refracted wave spews out from SNG on to the shelf – it becomes subjected to the effects of shoaling – with some amplification and further effects on way into estuaries. The SNG pattern is evident from the observed tidal excursion pattern and explains the general alignment of linear tidal ridges shown by 5 and 10 m isobaths. T Off (1963) described northwest-southeast aligned linear tidal ridges on the west of the SNG reflecting the observed tidal excursion pattern there. In the east, JM Coleman (1969) noted that the distributary mouths and the 5 m isobath are directed toward SNG. Tidal currents aligned to canyon/trough directions are reported to be present in the Indus Trough (EP Shepard and RF Dill 1966). In addition, alternating currents have been measured at the head of different canyons having the frequency of the dominant tidal motion (EP Shepard, NF Marshall, PA McLaughlin and GG Sullivan 1979). More than a century ago, J Fergusson (1863) remarked that the SNG is maintained by the scouring action of the convergence of two tidal currents rotating in opposite sense at the head of the canyon. As revealed in my Dissertation, the rotations of tidal currents are not in opposite sense – but have different excursion patterns. . . . 6. Tidal Oscillation, Currents and Residuals: The three sets of described measurements are fairly representative of the river hydrograph and the changing monsoonal wind pattern. In spite of a few exceptions, the data indicate some interesting hydrodynamic characteristics of the surveyed area. A clockwise turning tidal motion is observed at some stations while an erratic pattern is observed at others. The erratic pattern indicates a possible influence of coastal topography. The nearshore stations show rectilinear tidal motion in agreement with the channelised configurations of isobaths at those stations. Tidal motion types are indicated by showing the phase relationships between the observed water levels and the depth-mean tidal currents. An in-phase relation was observed at a station at the head of HT (as far south near Cox’s Bazar) – indicating a progressive wave-type tidal motion there. More shoreward, close to the entrance of Sandwip Channel, however, the tide develops into a standing wave type motion – shown by the phase lead of velocity by about 90o. Near SNG and in other deep waters – the processes of transitioning from progressive to standing wave type were observed with a phase lead of velocity by 1 hour or 29o. Standing wave-type oscillation was observed in inner shelf areas shoreward of 20 m isobath, indicating that coastal reflection of the incoming progressive tidal motion starts becoming effective shoreward from these depth-ranges. Tidal energy shown by variance of the depth-averaged tidal current was found to be a power function of tidal range: V = 0.07 - 0.02T+ 0.13T^2 (V = Variance; T = Tidal range). A depth-mean velocity vector variance of 2.17 m^2/s^2 was observed in Sandwip Channel near the entrance of Karnafuli River during a tidal range of 4.20 m (it is a macro-tidal environment). At the head of SNG for a tidal range of 1.20 m, the depth-mean velocity vector of 0.13 m^2/s^2 was observed (it is a meso-tidal environment). Variance of tidal currents is a measure of kinetic energy. Decomposition of flow vectors into orthogonal components shows that the Northings have higher amplitude, a leading phase and a higher variance than the Eastings. Comparison of the Northings over the vertical, at 1 m below surface and at 1 m above bottom, shows that the bottom velocity has lower amplitude but a leading phase than the surface velocity. The differences suggest that the near-bed sediment can have a different transport direction than the surface transport. . . . There we have it – a brief synopsis of coastal ocean current dynamics off rivermouths – where the actions of tide, seasonal riverine flow and wind conditions (for details see Chapter 2 of my Dissertation) define the force fields. This article is dedicated to celebrate the 51st anniversary of Bijoy Dibash – the Day on 16 December 1971 marks the Liberation of Bangladesh from the tyranny of Pakistani rule. Let freedom loving people from around the world come together to breathe the fresh air of emancipation – by being conscientious, heedful and diligent – whenever – wherever – whatever. And let us do that by remembering Charles Dickens (1812 – 1870), the British writer, novelist and social critic: have a heart that never hardens, and a temper that never tires, and a touch that never hurts. . . . The Koan of this piece: Be mindful what you think, say or do, because the Sun has the habit of not shining on one place for long . . . . . - by Dr. Dilip K. Barua, 16 December 2022 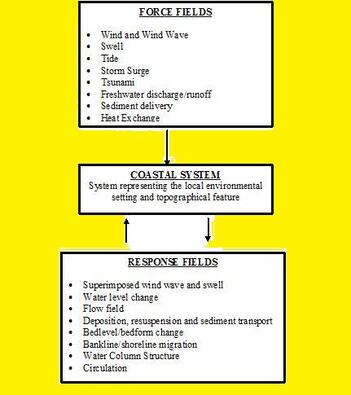 In this essay let us attempt to see in simple terms – the dynamics of coastal systems through a different scientific angle. This angle is the Force Field Theory (or ENERGY FIELD) first proposed by Michael Faraday (1791 – 1867) in 1845 (see The Quantum World; for a short introduction of the concept). A Coastal Engineer’s works, or widely the works of a Civil Engineer belong to the domain of Gravitational Force Field, GFF – formulated by Isaac Newton’s (1642 – 1727) Universal Law of Gravitation (ULG); and its dynamic characterization by Albert Einstein’s (1879 – 1955) General Theory of Relativity (see Einstein’s Unruly Hair). The GFF is a ubiquitous invisible field that affects everything on the Earth’s gravitation field. It defines all the downslope processes, and establishes the necessity of doing work to create upslope events (see Upslope Events and Downslope Processes). We vividly see the gravitational active force in fast flowing streams – and the gravitational restoration force in waves. In all of a Civil Engineer’s works – the universal gravitational acceleration ‘g’ is present (for all practical purposes, g = 9.81 m/s^2 on Earth’s surface). This value appears in almost every relation – with the mass or density (mass per unit volume) of a substance – together they define the weight of the gravitational force. To be in perspective, while GFF defines the Natural World; as a member of the Quantum Field (QF) family, the EMFF is ubiquitous and defines the world of electromagnetism.
Perhaps the dynamics of a coastal system – for that matter of any open system on Earth’s surface – can be viewed for convenience, in terms of external excitation or agitation forces on a system – and its internal balancing responses. Alternatively, this duo represents Action-Reaction Fields – in terms of Newton’s Equation of motion translated into Navier-Stokes Equation (see Seabed Roughness in Coastal Waters). I have presented an early version (shown in the image) of the force-response field concept quite a while ago while giving a seminar at UBC and later at the University of Central Florida – where force and response fields were shown separately defining the dynamics of a coastal system. For simplicity of discussions, I like to discuss the coastal dynamics in terms of five interactive Force Fields: (1) Metocean Force Field, MOFF; (2) Extraterrestrial Force Field, ETFF; (3) Land Drainage Force Field, LDFF; (4) Heat Exchange Force Field, HEFF; and (5) Frontal Wave Force Field, FWFF. The hydro-sediment-seabed dynamics responding to these imposed forces are discussed in these five force fields. I have also included a brief on the Structure Response Field (if structures are present). A different way of looking at the Force Field Systems is through the Hydrodynamic Entropy as proposed in Entropy and Everything Else. All the force fields impart energy into water – transforming its dynamic characteristics. One very obvious example is the effect of a Frontal Wave Force Field – in transforming the dynamic characteristics of the medium – e.g. an oscillatory wave transforming into a translatory wave – generating the cascade of dissipation processes. Let me attempt to refresh our understanding of a coastal system – based on other essays posted earlier: Coastal Water and Civil Engineering on our Seashore. A coastal system where the above interactive force fields function – is defined by two vertical boundaries (or the continuity of such boundaries into one or more depending on the type of physical barriers) and two horizontal boundaries (see more in Water Modeling piece). The horizontals are the water surface through which it interacts with wind – and the seabed, where it interacts with bottom resistance or reactive force. The verticals are: the open water boundary through which it interacts with its neighbors – and the shoreline of the topographical resistance or reactive force. One can also define other systems for the convenience of analysis and purpose (see Entropy and Everything Else). . . . 1. Metocean Force Field The water surface, a contiguous portion of the water column, or the whole water depth is the playground of MOFF. Atmospheric boundary layer generated by the turbulence of wind pressure and shear-stress – causes the formation of a water boundary layer defined by logarithmic decay of the imparted energy from the water surface down into the water column. Different aspects of this force field are elaborated in the Encyclopedia Chapters, Beaufort Wind Scale; Wave Hindcasting; and in the WIDCANVAS pieces: Ocean Waves; Transformation of Waves; Linear Waves; Nonlinear Waves; Spectral Waves; Waves – Height, Period and Length; Characterizing Wave Asymmetry and Storm Surge. Referring to them may prove useful while trying to understand the actions of MOFF. Further, I have tried to present wave motion dynamics in poetic terms – in the Ocean Waves piece. The MOFF forces the water body to respond in two ways with the GFF acting as the restoring force. To explain the two – I would rely on the Storm Surge piece posted earlier. The two are – the short surface wave and the long storm wave – both are generated by the dynamic pressure or kinetic energy exerted by MOFF; and their magnitudes are proportional to the square of the wind speed (Daniel Bernoulli, 1700 – 1782). The short surface wave transports the gained energy in progressive wave motions. Like the turbulent wind, these waves are highly irregular and spectral. The storm surge – on the other hand results from the hydrodynamic balance between the wind-induced water motion and the resistance of that motion by the coast. The result is the piling up of water at the coast – a standing long wave type oscillation. Along many coasts and bays around the world – MOFF causes seiche or meteo-tide that accentuates the high astronomical tide (see more on Storm Surge and Flood Barrier Systems). Following the wave pieces posted earlier, a clarification of short (or short legged) and long (or long legged) waves are necessary. To do that, let us revisit the 3 fundamental parameters: wave height H (simply the height from trough to crest), local wave length L or wave period T (measured simply from crest to crest, L in space and T in time), and the local still water depth d. A wave is a true short wave – when d/L > 0.5. A wave is a true long wave when d/L < 0.05. In between, a wave transitions from short to the long. Another important effect of MOFF is coastal upwelling and downwelling (see my 2017 Encyclopedia Chapter). These vertical water motions develop from a balance of wind-induced water motion, coastal resistance and the Coriolis Effect (see Characterizing Wave Asymmetry). Costal upwelling has a huge implication on modulating the weather pattern, and in fisheries population and abundance. . . . 2. Extraterrestrial Force Field The ETFF is caused by the Earth’s only satellite – the Moon, and the source of all our energy – the massive Sun (0.333 million times the mass of the Earth). The GFF of these three celestial masses defines the Earth-Moon-Sun System. An interaction takes place between the spinning Earth’s centrifugal outward force and the inward gravitational force of the system. All masses on Earth respond to the imposed forces – but the massive ocean water responds most (tidal effect on land masses is not effective, because land mass is heavy and rigid to distort; and atmospheric tide is hardly measurable because air density is too light). The result is the swelling of ocean water where outward force is the strongest and depletion where the outward force is the weakest. The generated wave is very large – a periodic rise and fall of the ocean water that has crests on the opposite sides and troughs in between. As the phase of the Earth-Moon-Sun system changes – the generated astronomical tidal wave propagates throughout the ocean. This ocean tide has a very small amplitude but a long period roughly equal to half day (see more on Ocean Waves). The strongest tide results when Moon-Sun acts in unison – resulting in fortnightly spring tide (during the Full and New Moons); and the weakest – the fortnightly neap tide occurs when Moon-Sun forces are out of phase (during the 1st and 3rd Quarters). The generated ocean tide – small in amplitude – propagating into the shallow coastal shelf, gets amplified into higher amplitudes (see more on Transformation of Waves). Further into the coastal basins of different configurations and sizes at different latitudinal distances from the Equator, different components of the tidal wave responds differently to the natural periods of the basins. The result is that each tidal basin shows its unique response to the forced tide – some are high or low, some are semi-diurnal or diurnal in period, yet others are mixed in character. Further, as pointed in earlier pieces, the transformation of a long wave (tide, tsunami and storm surge) – is modulated by the processes of funneling, resonance and shoaling. One spectacular example of such transformation is the vigorous tidal actions – with tides coming from two ends of the Discovery Passage in British Columbia (I had the opportunity to model this tidal phenomena using Mike21 hydrodynamic modeling suite). As outlined before in the Ocean Waves piece, the daily rise and fall of ocean water level attracted human imagination from ancient times, in particular because of its correlation with the phase of Moon. The workable explanations and predictions of the phenomenon, however came much later, and were worked out by many investigators. The notables among them were Galileo Galilei (1564 – 1642), Isaac Newton (1643 – 1727), Pierre-Simon Laplace (1749 – 1827) and Arthur Thomas Doodson (1890 – 1968). Their works led us to see tide as a composite mosaic of many tides – which can be decomposed into harmonic components of different periods, amplitudes and phases (that can be attributed to different generating forces). In very shallow water, some shallow-water harmonic components are highly amplified – giving birth to overtides and compound tides of different periods – different than the parent tide (e.g. my 1991 COPEDEC-PIANC paper). The rise and fall in water level is associated with oscillating horizontal movement of water causing tidal currents. . . . 3. Land Drainage Force Field In elaborating LDFF, I will rely mostly on WIDECANVAS pieces: Coastal River Delta and Managing Coastal Inlets; on the 2002 ASCE article Alluvial Deltas; on my Ph.D. Dissertation; on the 1990 IEB journal paper; on the 1995 JCR paper; and on the 1994 and 1990 Elsevier papers. The LDFF – mainly active in river mouths, estuaries and contiguous coastal ocean – comes with three distinct forcing characteristics: (1) the discharge of lighter density fresh/brackish water on to the ambient ocean salt water; (2) the volume and seasonality of this fresh water discharge; and (3) the volume, seasonality of the sediment discharge and sediment granular size distribution. Let us attempt to elaborate these three aspects of LDFF briefly. Density Driven Circulation. In absence of other force fields – riverine/estuarine fresh water flow rides on top of the heavy saline water – creating a stratified water column – with the top fresh water flowing outward into the sea – and bottom saline water moving in to balance the loss of fresh water. This process often with distinct halocline – termed as Estuarine Circulation – is ideal when the receiving coastal ocean is deep. When both MOFF and ETFF are active, the vertical stratification is destroyed by the MOFF induced mixing and circulation – and by tidal pumping of the ETFF. The effects often create horizontal stratification in shallow coastal oceans - with predominance of saline tide on one side, and fresh/brackish water on the other. As revealed in my 1990 works, a spectacular example of the horizontal stratification exists in the low-aspect-ratio (depth/width) coastal ocean at the Ganges-Brahmaputra-Meghna river mouth. Seasonal Fresh Water Discharge. Seasonality of the freshwater outflow has a substantial influence on the river-mouth hydrodynamics – from pushing the freshwater front out into the sea during the high-flow period – to the modification of tidal wave – to letting salt-water to intrude into the lower river reaches during the lean-flow period. As I have shown in my 1995 IEB paper, the Seasonality Index (mean monthly/mean annual) of the Ganges River varies from 0.2 during the dry season to 3.5 during the monsoon. With such a high seasonal fluctuation – and together with actions of other rivers of the Ganges-Brahmaputra-Meghna system, the estuarine front is pushed out into the open ocean during the monsoon (1990 IEB journal paper). Seasonal Sediment Delivery. Sediment transport is a power function of discharge – therefore the same scenarios of seasonality play a role in LDFF. However, there is a certain amount incoherence or hysteresis between water and sediment discharge (the 1995 IEB paper). Additionally, the characteristics of sediment granular distribution are also seasonal – determining the nature of delta progradation. . . . 4. Heat Exchange Force Field Compared to others, HEFF has a rather subtle – even negligible effect on the coastal hydrodynamics. Therefore no term related to HEFF appears in the general description of the Navier-Stokes Hydrodynamic Equation (e.g. in 2D depth-averaged modeling; but must account for it in 3D modeling). For aquatic lives – however, HEFF is very important – some are dependent on and look for warm waters – while for others cold water is important. Therefore - HEFF appears as an important parameter in the Water Quality Modeling. The water body interacts with the air-temperature above its surface – in gains or losses of heat according to the 2nd Law of Thermodynamics (e.g. high to low, one-way process; see Entropy and Everything Else). This process occurs in the Thermodynamic Force Field or TDFF domain (see The Quantum World) - in molecular diffusion mode. When hydrodynamic actions are strong due to such factors as wind and current - an extra two-way mixing mechanism is added, thus augmenting the HEFF processes. The HEFF process primarily gives rise to sharp lines of temperature difference or thermocline in the capacity of micro-circulation. Hydrodynamic actions in turbulent eddies (see Turbulence) is responsible for mixing of thermally stratified water bodies - destroying the thermocline in the process. Also, fast flowing streams or high energy fluid motions do give birth to heat in frictional dissipation of energy at the bed. I only became aware of HEFF when I was working on a project tasked to assess hydrodynamic characteristics of Lynn Canal, Alaska. This deep U-shaped fjord is stratified with distinguishable thermocline. Analyses of long time-series data have revealed how the water column is thermally stratified with the nature of stratification changing shape and gradient responding to seasonal heat gain during Spring-Summer – and heat loss during Autumn-Winter. The investigated area of the Lynn Canal system is characterized by a stable thermal minimum zone at a depth of about 140 m – below which a rather stable layer of positive temperature-gradient (temperature increases with depth) resides – which remain rather irresponsive to the surface heat gain or loss at the surface. The top layer from surface to the thermal minimum, on the other hand is characterized by negative temperature gradient (temperature decreases with depth) – that changes in response to seasonal heat grain or loss. The implication of such a stratification is that dynamic mixing and circulation is confined within the top layer – with the rest of deep water column literally not knowing what happens at the top. . . . 5. Frontal Wave Force Field The FWFF is the most energetic and dramatic of all the coastal force fields. It generally pertains to the processes of Hydrodynamic Entropy – a term coined in Entropy and Everything Else. It is generated by the sudden release of built-up pressures or accumulated energy (the closest analogy of FWFF is the sonic boom in acoustics) by some triggers. Such accumulation of hydrodynamic energy could occur for many different reasons – impoundment and obstruction are two of them. But basically it happens when the rate of accumulation far exceeds the dissipation processes. The fundamentals of the FWFF are same as what are discussed in the Nature’s Action and Upslope Events and Downslope Processes. Let us attempt to understand the coastal FWFFs in simple terms. The four of them are: Tidal Bore, Tsunami, Flood Barrier Collapse and Storm Surge. Breaking of waves (see The Surf Zone) also creates FWFF – occurring rather regularly, the phenomenon defines beach evolution – in erosion, sedimentation and longshore sand transport. Many episodes of FWFF take people and authorities by surprise – as they are random in occurrence and remain beyond the purview of conventional forecasting. The released FWFF pressure wave containing huge amounts of energy propagates at a celerity or speed of supercritical flow (c = square root of the product of ‘g’ and water depth; at 1-m water depth c = 3.1 m/s; compare that with the tranquil flow speed in the order of 0.5 m/s). The leading edge speed is even higher than supercritical flow ≈ some 1.4 to 2*c. A wave with such a high speed could propagate upstream, and cross and overtake obstacles and transports huge load of debris and sediments. The most spectacular examples of this incredible speed – are the recent 2004 Indonesia tsunami and the 2011 Japan tsunami (many of us witnessed the havoc of them in live coverage). Explained further and see more in Tsunami and Tsunami Forces. Tidal Bore. USGS Circular 1022 (1988) presented a catalogue of world-wide distribution of tidal bores. Tidal bores form during spring tides when the range is the highest. With the combined affects of shoaling and funneling – the propagating tide becomes highly asymmetric so much so that at a certain time maintaining the wave-form becomes unsustainable – the result is the breaking of the accumulated pressures – giving birth to tidal bores. As happens with other long wave transformations – the accumulation lets the integration of all different component tidal frequencies into one pressure wave. The propagating bore with its breaking sound is very spectacular – and the phenomenon has given birth to wave-surfing and tourist attractions – with people flocking together to witness this Nature’s action. While on an investigation vessel, I was once in the middle of tidal bores in a tidal channel in Bangladesh southeast coast. With bores coming from two different directions, very low water suddenly rose to a high level as the bore passed. If one plots the tidal height and current – the sudden rise of these two parameters becomes very vivid. While tidal bores are spectacular to watch, they also pose navigation hazards to small vessels. Tidal bores transports sediments and reshuffles alluvial sand to create islets and scour holes within a very short period of time. Tsunami. Let me highlight this FWFF based on the WIDECANVAS piece, Tsunami and Tsunami Forces and my 2006 Tsunami paper and 2008 ASCE article. Tsunami is a series of impulsive waves generated by sudden rupture of underwater earth’s crust, or by rapid slides of large landmass into water, or by sudden change in local atmospheric pressure (a phenomenon of MOFF). Following the alignment of disturbance, tsunamis radiate out directionally traveling long distances to reach coastal land – far and near. Tsunami characteristics change in response to the configurations of an enclosed basin or harbor. Like all waves, a small tsunami in deep water shoals to monstrous waves as it propagates into the shallow water. After breaking, Tsunami Run-ups flood coastal lands with enormous inbound and outbound speeds causing havoc and destruction. The arrival of Tsunami crest is preceded by the huge draw down or Sea Level Suck Out associated with the Tsunami trough. This phenomenon sucks out things from the shore out into the sea - exposing shoreline features - leaving many aquatic lives stranded in air. It catches offshore boats off-guard - and tragedies happen when people rush out to catch the stranded fishes. Flood Barrier Collapse. In the Flood Barrier Systems, we have seen different aspects of water barriers. Such barriers are designed to hold the propagating storm surges and other flood waves – to protect areas behind them. The stoppage of propagating waves – lets accumulation and integration of pressures causing a very high turning moment on the barrier systems. The barriers while designed to protect townships and properties – are also like a human-made hazard – in a sense that they pose high risk. But the benefit of taking the risk is worth, because letting the frequent onslaught and inundation has the action of taking a bite on people’s livelihoods. The catastrophic failure of the flood barrier system protecting New Orleans – during Hurricane Katrina in 2005 – is one of the reminders of how vulnerable a flood barrier can be. Storm Surge. Unlike other waves, storm surge (see more on Storm Surge) generated by Hurricane winds most often does not have a definite wave form – its crest is more pronounced than the trough. It develops, as a Hurricane low pressure system moves along or across on to a shore. The low pressure at the eye of the Hurricane causes reciprocal rise in water level, and together with wind-shear the system causes huge water mass to pile up along the coast – at the right side of the propagating storm in the northern hemisphere. The storm surge (note that a storm surge is not monochromatic, therefore some frequencies may resonate to the basin natural frequency) superimposed on astronomical tide generates the storm tide. The peak storm tide – a superimposition of high tide and peak storm surge – combined with high waves, causes large coastal flooding, erosion and damages.
. . . Let me finish this piece with a Koan: People are the most important institution. Irrespective of the governing system – if those in power fail to uphold the trust and confidence of this institution – of people’s aspiration and wellbeing – then the governance turns into tyranny. . . . . . - by Dr. Dilip K. Barua, 25 August 2021
There is nothing noble in being superior to your fellow man; true nobility is being superior to your former self. Who can be a better person than Ernest Hemingway (1899 – 1961) – to write this in his skillful way of crafting words in a lucid and attractive style? Sayings similar to this have been penned down in several pieces of WIDECANVAS in different contexts – not to advance is to fall back – change and refinement as a show of intelligence – maturity – adaptation . . . etc. But Hemingway touched upon a very important aspect of human mind. That being taken over by superiority or inferiority complex (see aspects of it, in Some Difficult Things) – inhibits a person’s ability to think and function normally. This piece is nothing about these complexes – but on something that define Nature – in this case, the transmission or propagation of errors or uncertainties in wave loadings on coastal structures. Uncertainty (U), in its simplest term, is just the lack of surety or absolute confidence in something.
Uncertainty Propagation (UP) refers to the transfer of uncertainties from the independent variables into the dependent variable – simply put, from the known to the unknown. It is transferred in an equation or relation – from the individual variables on right hand side – into the dependent variable on the left. More commonly the propagation process is referred to as error propagation. The two – error and uncertainty are often used interchangeably. In quantitative terms, while error refers to the difference between the measured and the true value – uncertainty refers to the deviation of an individual measurement from the arithmetic mean of a set of measurements. As we shall see, the magnitude of propagated uncertainty is a function of the type of equation (e.g. linear, non-linear, exponential, logarithmic, etc). . . . 1. Uncertainty Fundamentals Uncertainty of a parameter implies that, if it is measured repeatedly – one would find that there is no single value – rather a range of random values accrue that deviate from the arithmetic mean (AM, µ) of the measured set. One needs a method or standardization to characterize the scattered deviations. If the deviations are distributed symmetrically about the arithmetic mean – then a Gaussian (German mathematician Carl Freidrich Gauss, 1777 – 1855) bell-shaped curve can be fitted. One property of such a distribution is defined as the Standard Deviation (SD). This is estimated as the square root of variance (defined as the mean of all deviations squared). If SD is normalized by dividing it with AM – the GD turns into Normal Distribution or ND. The normalized SD, σ/µ, termed as the Coefficient of Variation (CV) – is SD relative to AM. Its distribution follows the symmetry about the mean – and as a fraction or percentage, it covers both sides of the mean. It is like the unit of standard deviation – e.g. 1SD unit saying that 68.2% of the data are scattered on both sides of the mean. A high value of CV is the indication of a large scatter about the mean. CVs are due to nature of the variable in their random response to different forcing functions or kinetic energy (see Turbulence) – and are therefore termed as random uncertainty or simply uncertainty (see more on Uncertainty and Risk). It is the signature characteristic of the variable – and is due to many other factors including the applied measuring or sampling methods. Not all variables follow the Gaussian distribution (GD), however. For example, a discrete random variable, like an episodic earthquake or tsunami event – are sparse and do not follow the rules of continuity, and is best described by Poisson Distribution (PD, in honor of French Mathematician Simeon Denis Poisson, 1781 – 1840). An ideal example of a continuous variable that follows ND is coastal water level. In this piece, all applied variables are assumed to follow ND. Here are some typical CVs from R Soulsby (1997): water density, ±0.2%; kinematic water viscosity, ±10%; sediment density, ±2%; sediment grain diameter, ±20%; water depth, ±5%; current speed, ±10%; current direction, ±10o; significant wave height, ±10%; wave period, ±10%; and wave direction, ±15o. Error or uncertainty propagation technique has been in use for long time dating back to the now known method since 1974 (G Dalquist and A Bjorck). The most recent treatment of the subject can be found in BN Taylor and CE Kuyatt (1994) and in AIAA 1998 (The American Institute of Aeronautics and Astronautics). The propagated uncertainty has nothing to do with the scientific merit of a relation or equation; it is rather due to the characteristic or signature uncertainties of the independent variables – which according to the UP principle must propagate or transmit onto the dependent variable. . . . 2. Propagation Basics This piece is primarily based on four pieces posted earlier: Uncertainty and Risk; Wave Forces on Slender Structures; Breakwater; and The World of Numbers and Chances; and three of my papers:
Before moving on, let me try to demonstrate how UP principle works – by discussing a simple example. Suppose, we consider an equation, X = Y^2 * Z. Let us say, the variables Y and Z on the right hand side of the equation have known CVs: ± y, and ± z, respectively. How to estimate the CV of X? According to the UP principle, the CV of X can be determined as the square root of x^2 = 2^2*y^2 + z^2. As an example, suppose, y = ±10%, and z = ±5%; then x must be equal to 20.62%. Further, a pertinent question must be answered. Why Uncertainty? or Why Uncertainty Propagation? The relevance of the questions stems from the quests to develop confidence of the relations or equations one uses to compute and estimate parameters for everything – from the science of Nature to Social Interactions to Engineering and Technology. These relations developed by investigators after painstaking pursuits convey theories and principles mostly on deterministic paradigm. But, things in Nature are hardly deterministic – which means the independent variables on which a relation is based – suffer from uncertainties of some kind due to their stochastic characteristics and variability. These uncertainties associated with the independent variables must be accounted for in the dependent variable or computed unknown parameter. Uncertainty propagation method developed over a period of many years – gives answer to the questions (see more on Uncertainty and Risk, and The World of Numbers and Chances). In engineering design processes, the traditional method of accounting for uncertainty is done simply by including some redundancy in the system – by the so-called factors of safety – conspicuously described and/or inconspicuously embedded in some practices (for example, using maximum load and minimum strength; and summation of different loads together although they may not occur simultaneously). Further elaboration on coastal design processes can be found in Oumeraci et al (1999), Burcharth (2003) and Pilarczyk (2003). They scaled the processes of design as: Level 0 – deterministic approach; Level I – quasi-probabilistic approach; Level II – approximate probabilistic approach; and Level III – fully probabilistic approach. In the Level 0 approach, parameter uncertainties are not accounted for, instead experience and professional judgment are relied upon to implant redundancy. This practice as a way of developing confidence or assurance – represents in reality – a process of introducing another layer of uncertainty – partly because of heuristics associated with judgments. Or in another interpretation, it amounts to over-designing structure elements at the expense of high cost. For the other three Levels, a load-strength reliability function is defined in different scales to account for parameter uncertainties. A note on significant wave height uncertainty is warranted. Although a typical ±10% is recommended by Soulsby, in reality the uncertainty can be varied. The reasons can be traced to how the local design significant wave height is estimated. Some likely methods that affect uncertainty are: (1) the duration, resolution and proximity of measurements to the structure; (2) extremal analysis of measurements to derive design waves; (3) in absence of measurements, applied analytical hindcasting or numerical methods to estimate wave parameters; and (4) applied wave transformation routines or modeling. Due to these diverse factors affecting uncertainty, instead of considering one uncertainty, this piece covers a range from10 to 30%. . . . 3. Uncertainty of Wave Loading on a Vertical Pile This portion of the piece starts with 2008 ISOPE paper and Wave Forces on Slender Structures. Unbroken waves passing across the location of a slender structure (when L/D < 1/5; L is local wave length and D is structure dimension perpendicular to the direction of force) cause two different types of horizontal forces on it. The basis of determining them is the Morison equation (Morison and others 1950). Known as the drag force in the direction of velocity, the first is due to the difference in local horizontal velocity head or dynamic pressure between the stoss and the wake sides of structure. The second, the inertial force is caused by the resistance of structure to the local horizontal water particle acceleration. Both of the Morison Forces have their roots in Bernoulli Theorem (Daniel Bernoulli; 1700 – 1782) – and as one can imagine, they are a function of water density – and of course, the structure size. The horizontal Drag Force: a function of water density, structure dimension perpendicular to the flow, water particle orbital velocity squared, and a drag coefficient. The horizontal Inertial Force: a function of water density, structure cross-sectional area, water particle orbital acceleration, and an inertial coefficient. To demonstrate UP of wave loadings at the water surface on a cylindrical vertical pile of 1 meter diameter – this piece relies on the same example wave discussed in Linear Waves; Nonlinear Waves; Spectral Waves; Waves – Height, Period and Length and Characterizing Wave Asymmetry. This wave, H= 1.0 m; T = 10 second; d = 10 m; has a local wave length, L = 70.9 m and Ursell Number (Fritz Joseph Ursell; 1923 – 2012) = 5.1; indicating that the wave can be treated as a linear wave at this depth. Other used and estimated parameters are: water density = 1025 kg/m^3; amplitude of horizontal orbital velocity at surface = 0.56 m/s; and amplitude of horizontal orbital acceleration at surface = 0.44 m/s^2. In addition, while using most typical uncertainties proposed by Soulsby – the Us of wave length, orbital velocity and acceleration have no typical values – therefore they are derived in the 2011 paper and in this piece applying the basic UP principle. The results of uncertainties in wave loadings are shown in the two presented images – one for the drag force (UDF), the other for inertial force (UIF). They are shown as a function of uncertainties in measured wave heights (U_H) for U_water density = 0.2% and U_linear dimension = 5%, with estimated U_cylindrical pile area = 10%. Since the uncertainties of coefficients (U_Cd and U_Cm) are not known, the images show three cases of them, 10%, 20% and 30%. Here are some numbers for U_H = 10% and 30%.
. . . 4. Uncertainty of Wave Loading on Breakwater Armor Stones This portion of the piece primarily depends on materials developed and presented in the Breakwater (BW) piece posted earlier, as wells as on my 2011 paper. The state-of-the-art techniques in determining armor stone masses or sizes of rubble-mound breakwater and shore protection measures – rely either on Hudson Equation (RY Hudson 1958) or on VDM Formula (JW Van der Meer 1988). The applicability and relative merits of the two methods are elaborated in the Breakwater piece. For simplicity of analysis, I will focus on the uncertainty of Hudson Equation. This equation relates Stability Number to the product of a stability coefficient (KD) and a BW side slope factor. The equation provides estimates of median armor stone mass as: a product of the stone density and wave height cubed – divided by the product of KD, side slope factor, and relative stone density cubed. It is assumed that armor stone is forced by H = 1.0 m on the BW seaside slope = 1V:2H; with stone density = 2650 kg/m^3 and water density = 1025 kg/m^3 giving a relative stone density = 2.59. The uncertainties of relative density and side slope factor are not known, they are estimated at 2.01% and 7.1% using basic UP principle. The crux of the problem appears on defining the KD values. The recommended KDs vary from 1.6 for breaking to 4.0 for non-breaking wave forcing (USACE, 1984). Melby and Mlaker (1997) reported that the KD values have uncertainty of some ±25%. In this piece the uncertainties median armor stone mass U_M50 for KD uncertainties ranging from ±10% to ±25% are investigated. Some estimated numbers are:
. . . The Koan of this piece on this International Jazz Day: What seems to be perfect to an ordinary eye – is never finished, never perfect in the creator’s eye. The creative works continuously explore, experiment and search for something – that never comes to the satisfaction of the creator. . . . . . - by Dr. Dilip K. Barua, 30 April 2021  A harbor is a water basin of tranquil or tolerable wave and current climate, and of sufficient water depth in which a maritime or inland vessel (let us use this general term, but when Dead Weight Tonnage or DWT ≥ 500, a vessel is known as a ship) can operate safely. Maritime harbors are selected from the deep shoreline areas sheltered naturally, or are created artificially (see Flood Barrier Systems). The artificial harbors are configured and engineered within an ambient water body at the shoreline by dredging and installing suitable structures (see Breakwater). The purpose in each case is to locate a maritime port or marina within it (see Ship Motion and Mooring Restraints; and Propwash). For the convenience of design and operation, a harbor is classified and distinguished as deep-draft (water depth > 15 ft or 4.6 m), and shallow-draft or small-craft (water depth < 15 ft or 4.6 m). Many artificial harbors have one inlet to allow influx and efflux of water and sediment into the basin (a semi-enclosed basin that allows restricted/controlled entry and exit of matter and energy, see Upslope Events and Downslope Processes); and entry and exit of vessels. The layout of the structure – and the location, width and depth of the approach channel as well as of the harbor itself are designed by addressing such constraints as – ambient wave, current and sediment climates, and the largest allowable vessel designed to call at the port.
. . . In this piece, let us attempt to discuss and understand the sedimentation rates of harbors in simple terms. Sediment transport dynamics and sedimentation pose a complicated problem. But ballpark estimates and numbers are always handy and useful to conceive and study the feasibility of a project. To that end, some methods and pieces of data are selected and blended in this piece. The purpose is to demonstrate the usefulness of some simple analytical models that can be used as a handy tool to picture a high-level impression of possible harbor sedimentation. The magnitude of sedimentation problem can be appreciated if one considers worldwide dredging operations. Maintaining enough water depth within the harbor and keeping the approach channels navigable – are some of the requirements that let flourishing of huge dredging industries. These two major demands, together with the erosion prevention and value-adding beach nourishment works, and others – have yielded the global dredging industry to an annual turnover of some $5.6 billion. I will try to come back to discussing different interesting aspects of dredging at a later time. Among others, this piece is primarily based on: RB Krone 1962; Delft Hydraulics publications (E Allersma 1982; WD Eysink and H Vermass 1983 and WD Eysink 1989); R Soulsby 1997; USACE 2002 EM 1110-2-1100 (Part III) and 2006 EM 1110-2-1110 (Part II); I Smith 2006; and my own works on fine sediments and sedimentation (Fluid Mud 2008; and Settling Velocity of Natural Sediments 2004) published in the Journal of Hydraulic Engineering, and Journal of Waterway, Port, Coastal and Ocean Engineering, respectively; Seabed Roughness; and two papers presented at the International Symposiums on Coastal Ocean Space Utilization: COSU 1995 and COSU 1993, and my paper at the 24th International Conference on Coastal Engineering, Kobe, Japan, ICCE 1994. The Hydraulics of Sediment Transport and Resistance to Flow posted earlier laid out some fundamentals of sediment behavior and transport. . . . 1. Configuring Harbor Layout and Tidal Hystereisis Configuring the layout of a harbor entrance needs careful optimization exercises and analyses – on the one hand, it has to provide effective diffractive energy dissipation of incoming waves – on the other, it has to minimize the formation and strength of current eddies at the entrance, and sedimentation inside the basin. Filling and emptying tidal currents at a harbor entrance are usually an order of magnitude less than the ambient tidal current. Their magnitudes depend on the size of the basin and entrance. Eddies – more vigorous during changing current directions – are undesirable for at least two primary reasons. The first is to minimize navigation hazards – to vessels entering and leaving the port. The second is to minimize scour and formation of sandy bars. Exercises to engineer a detailed and optimal layout include physical scale modeling and/or numerical modeling. Such exercises, especially the efforts of numerical modeling (see Water Modeling) are becoming increasingly common not only for optimizing harbor entrance layout, but also for visualizing the sediment morphodynamics, sedimentation and other aspects of harbor hydraulics (e.g. Ports 2013 paper). Before moving on, let us have some words on tidal action. It is assumed that actions attributed to short-waves (see Ocean Waves and Linear Waves) and vessel generated wake-waves are minimal – a valid assumption for all harbors. The main concern of harbor sedimentation processes is the behavior of Suspended Sediment Concentration (SSC) that has a positive gradient from low at top to high at bottom of the water column. As flood and ebb currents reach threshold for erosion and resuspension during a tidal period – sediments are picked up from the seabed and are transported (coarser fraction close to the bed; fines up in the water column) back and forth by the current. Similar but opposite episodes happen, as flood and ebb currents slow down to reach deposition threshold. Suspended sediments have the opportunity to settle down during such slack water periods (SWP) – with more chances for sediments close to the bed than those up in the water column. However, there is often a settlement lag or incoherence between the slack water and actual deposition (see more in my 1990 Elsevier paper). . . . 2. Harbor Sedimentation Problems Let us now dive down into the core issue of this piece. A harbor faces at least two types of major sedimentation problems. The first is the formation of localized shoals or sandbars at and around the entrance due to the scouring actions of eddies, and the sudden drop in flow velocities. These shoals mostly of sandy materials are often attached to the shoreline as a side bar or develop as middle bar(s). They mostly develop when the harbor entrance is located on littoral shores (see Managing Coastal Inlets) – and are usually termed as flood-tidal and ebb-tidal deltas (see Coastal River Delta and Managing Coastal Inlets). The dynamics of such sandy shoals, bars or deltas can best be discerned from the piece on The Hydraulics of Sediment Transport. The focus of this piece is on the second type of sedimentation problem. It is the sedimentation of fine sediments within the harbor basin. This sedimentation (a phenomenon of suspended sediments having very low settling velocities) is somewhat uniform due to the relatively weak circulation within the harbor basin – but is often less in areas of relatively high currents than in remote areas of stagnant water. It is highly problematic when a harbor is located within Turbidity Maximum (TM) zone (1990 Elsevier paper). The presence of TM in the tide-dominated east shore channels and waterways of the Ganges-Brahmaputra-Meghna (GBM) River mouth has shown very high siltation rates of fine sediments (1997 Taylor & Francis paper). Observations at the mouth of Karnafuli River estuary showed a positive correlation between the Surface Suspended Sediment Concentration (SSSC) and tidal range (TR) – indicating that the resuspension actions of tidal currents are directly related to tidal range. This correlation ends up yielding an exponential relation between SSSC and TR (ICCE 1994). The fitted relation shows, for example, that at mean neap-tidal TR = 1.7 m, SSSC = 154 mg/L; and at mean spring tidal TR = 3.8 m, SSSC = 1912 mg/L. The gradual but slow filling up of the basin is highly dependent on the concentration of sediment suspended (in textures of fine sand, silt and clay) of influx water. For the convenience of discussion, let us spilt the piece in two: (1) the first is on sedimentation of granular (silt-sized particles) materials; and (2) the second is on sedimentation of silty/clayey materials that are affected by aggregation and flocculation. The provided estimates represent only a high-level first-order magnitude – afforded by some approximations and assumptions. And to be simple yet realistic of a deep-draft harbor, let us use most of the same inlet/basin/tide parameters (inlet depth 15 m; harbor depth 10 m; semi-diurnal tidal period 12.42 hours; and tidal amplitude 1 m) as described in Managing Coastal Inlets – for a large harbor area of 1 million square meter; and an inlet length and width of 100 m and 300 m, respectively. A tide of this amplitude at 15 m water depth, causes a passing peak depth-averaged current of about 0.81 m/s in front of the harbor. A rough estimate shows that for a harbor of this size at this tidal condition – the turnover time (the time required to tidal flushing out 63% of the harbor water volume) is about 3.2 days. . . . 3. Sedimentation of Suspended Particulates Let us attempt to make a simple first-order estimate for a single inlet harbor that has no freshwater drainage into it. It is assumed the system is well-mixed vertically without any density stratification. In such harbors, the volumetric sedimentation rates can simply be expressed as a linear function of sediment influx, and a factor attributed to the fraction of sediments that actually settles into the basin. It is also a linear and reciprocal function of dry bulk density of the suspended deposits. One can also assign a calibration factor to account for uncertainty of assumptions, approximations, the approach itself, and for the spatial and temporal distributions of sedimentation. The first, the sediment influx is a function of SSC that are transported by the total volume of water exchanged during the tidal cycle. This volume, in turn depends on the tidal prism forced into the harbor, and the horizontal exchange of water induced by passing current at the inlet entrance (a function of passing current, inlet width and depth). The Volumetric Suspended Sediment Concentration (VSSC) is reciprocal to the porosity of water-sediment mixture (the ratio of void volume filled with water to the total volume). When VSSC is multiplied by the density of sediment particulates, the Mass Suspended Sediment Concentration (MSSC) is obtained. The second, the settling factor is a function of (1) particle settling velocity, (2) average basin water depth, (3) threshold velocity for sediment settlement, and (4) the window of time or SWP during a tidal cycle when settling occurs. In this simple example, one silt-sized particulate is considered – the median diameter of which is assumed as 1/32 mm or 0.03125 mm (corresponding to the demarcation defining the coarse and medium silts) – with no sand content. The settling velocity of this fine silty material is 0.084 cm/s (according to Rubey 1933; see 2004). In the density of sediment-water mixture, let us assume the sediment granular density as 2650 kg/m^3 (typical of silty materials of quartz mineral origin) – and the water density as 1025 kg/m^3 (typical of most coastal water; note this density may be high for the some of the considered cases, but the errors caused by using different water densities are very negligible, see Coastal Water). For all-silt suspended sediment, the dry bulk density of the deposit – is a function of these two parameters, as well as of packing. Having laid out these fundamental parameters, let us attempt to make some estimates. The included image shows the annual volume of silt-sized sediment deposits as a function of MSSC. It is applicable for parameters discussed earlier with the assumption that the time window available for settling SWP = 10 min during the tidal cycle. As an example, if an MSSC of 1325 mg/L persists throughout the year, the total annual deposit volume will be about 0.10 million m^3. Such a sedimentation rate is no reflection – however, of the usual differences and variations expected in space (e.g. flowing channel vs sheltered areas) and in time (e.g. spring vs neap tides; and dry vs wet season). Based on actual field conditions, sedimentation volume (which can be discerned from dredged volumes; or from repeated bathymetric surveys) and harbor activities (caused by vessel propwash with consequent erosion, resuspension and deposition of sediments; see Propwash), one can apply a factor to calibrate the estimated sedimentation. . . . 4. Sedimentation of Aggregated Particulates This part of the piece is based mostly on my published papers: the 1994 ICCE 24th; and the COSU 1993 and 1995 papers. The published works are based on some site-specific information; and are therefore primarily applicable for situations and conditions in which they were derived. But the approach and methodology can be applied elsewhere with some assumptions for cases – of tide-dominated estuaries, bays and waterways dominated by fine seabed sediments. Let us attempt to see some applications of the gained experience in simple terms. They are supplemented by my discussions in 2004 and 2008 publications. The first approach relies on ICCE 1994 paper and the Fluid Mud 2008 discussion. To be realistic of the annual variability, one needs to consider both spring-neap tidal and seasonal parameters. To that end, the used values are: neap and spring tidal TRs as 1.7 m and 4.0 m, respectively, and the wet and dry season salinities as 2.0 ppt (parts per thousand) and 4.0 ppt, respectively. Another assumption has to be made – it is on SWP during which tidal currents slows down below the sedimentation threshold. Experience tells that neap tidal SWP is longer than the spring tidal SWP; therefore let us assume neap SWP = 15 min and spring SWP = 5 min. Let us also consider the neap and spring tidal SSSC as the initial concentrations required for the relations proposed in 2008. With these assumptions and applied parameters as if they persist throughout the year, the total annual sedimentation volume turns out to be about 0.39 million m^3. The second approach (COSU 1993 and 1995) is primarily based on the modeled sedimentation rates observed in some areas of the GBM mouth – therefore is highly site specific. They were done in contexts of determining the height of sedimentation at which impoldering (a Dutch term referring to the process of reclaiming and developing the silted coastal shores for rice farming – by closing and isolating the area from saline coastal water flooding by installing earthen dikes and sluices) can be initiated. In this case the used relation giving annual sedimentation height relies on initial water depth, and a coefficient. Let me cite examples for two sites – in one, mainly dominated by tide and muddy seabed; and the other dominated by GBM fresh water flow and sand/silty seabed. The measured SSC at the two sites differ by an order of magnitude – the first is about 4230 mg/L, the second is about 126 mg/L. Note that the first area was very sheltered – which means, water flooding the tidal flat and gullies highly laden with SSC was ideal for settling sediments. If one attempts to extrapolate the estimated deposition to the whole harbor basin – applying the assumed conditions and circumstances, the estimated volumes turns out to be 5.42 million m^3 and 0.23 million m^3, respectively. In summary, the discussed ballpark estimates varying from 0.10 to 0.39 million m^3 – present a clue on what sedimentation to expect when planning the feasibility of a harbor. One referral case in point (see Ports 2013 paper) is the modeled annual sedimentation volume of 0.025 million m^3 – concentrated mostly in entrance areas of the Salt Ponds Inlet harbor (size, 0.1 million m^2) in Virginia, USA. This was the case of a small harbor of sedimentary environment dominated by fine sands, not adequately sheltered from wave actions. The estimate of 5.42 million m^3 – rather unusually high, is an indication of some very calm and stagnant areas – flooded by very high SSC of flocculated sediments. Such a situation is unlikely to happen in harbor conditions. . . . Before finishing I like to tell a story the Buddha (624 – 544 BCE) told to a congregation of monks and lay people. He did this in context of the 4th Buddhist precept of Right Speech (see Revisiting the Jataka Morals – 2). Once an angry and hateful person used very harsh and abusive words to the Buddha. Instead of getting provoked, the Buddha calmly listened and told the man to take back his abusive outburst. The man was dumbfounded hearing such an unusual reaction. The Buddha then said: Hold it there. If a person gives a gift to another, and if the second person refuses to accept the gift, to whom the gift belongs? The man replied: it belongs to the first person. The Buddha said: so, my friend you must take back the abusive language you have used, because it belongs to you and I refuse to accept it. Then the Buddha delivered some words of wisdom to the congregation: if someone spits against the sky, the spittle returns back to the spitter. So, be mindful. If you use an abusive or unwholesome speech, it gets back at you. . . . . . - by Dr. Dilip K. Barua, 23 November 2020 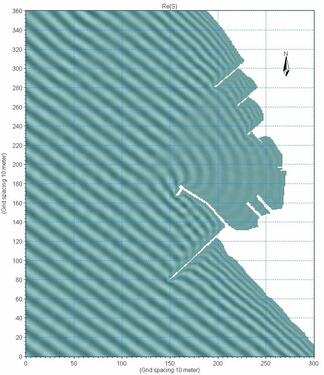 Ever since the 1978 failure of a massive breakwater (BW) in Port Sines, Portugal – coastal engineers around the world went back to reviewing the BW design approaches and methods. During my studies at Delft in 1982 – the event and the possible lapses and causes of its failure – came for discussions again and again in coastal engineering lectures. The Sines Deepwater (~ 50 m) BW was designed and constructed of massive 42 tonne armor-layer dolos (dolos are pre-fab concrete units, designed to achieve good interlocks and stability when placed randomly – each unit has three stems, the central and the two twisted ones on ends) to withstand waves up to 100-year extreme of 11 m high significant wave (see Spectral Waves for definition). But near the end of the construction period – a storm that registered a lower wave height, dislodged about 2/3rds of the units – and some subsequent less powerful storms did the rest of the work by destroying the BW.
The risk of failure, the scale and cost of such massive structures – have generated renewed research interests in coastal labs around the world. Physical scale modeling tests – such as those in the massive Delta Flume in Emmeloord (the Netherlands), and in the CERC (Coastal Engineering Research Center) facilities in Vicksburg, Mississippi were some of the examples. The efforts resulted in the refinement of existing formulae and coefficients, and yielded new ones. . . . In this piece let us attempt to understand some interesting aspects of BW engineering. Engineering literature is full of materials on various aspects of BW planning, loading, stability, designs, and effects assessments. Among them, the following lists have most of the resources one needs for breakwater engineering: (1) Random Seas and Design of Maritime Structures (Y Goda 2000); the USACE (United States Army Corps of Engineers) (2) 1984 Shore Protection Manual (SPM); and its reincarnation, Coastal Engineering Manuals (CEM): (3) the 2002 CEM (EM 1110-2-1100 Part II; Chap 8 – Hydrodynamic Analysis and Design Conditions), (4) the 2006 CEM (EM 1110-2-1100 Part VI; Chap 5 – Fundamentals of Design, and Chap 6 – Reliability Based Design of Coastal Structures); (5) the 2007 Rock Manual (C683, the use of rock in hydraulic engineering, 2nd ed.) of EUROCODE, CIRIA (Construction Industry Research and Information Association) and CUR (Civil Engineering Research and Codes, the Netherlands); the JW Van der Meer publications, starting with his (6) 1988 Ph.D. Diss. (Rock slopes and gravel beaches under wave attack, Delft Univ. of Technology, the Netherlands, Delft Publication No. 396); and his (7) 1992 Delft Lecture Note, Conceptual Design of Rubble Mound Breakwaters; (8) RY Hudson 1958 (Design of quarry-stone cover layers of rubble-mound breakwaters, hydraulic laboratory investigation, Research Report 2-2, Waterways Experiment Station, Vicksburg, MS); and (9) R Iribarren 1938 (Una Formula Para el Calculo de los Digues de Escollera, Technical Report HE 116-295, University of California, Berkeley, CA). On 2D Wave Diffraction Modeling suite: (10) the 2005 Bouss-2D Wave Model in SMS, ERDC/CHL CHETN-I-69/70; (11) the 2007 Delft3D-Wave, TU Delft and Delft Hydraulics; and (12) the 2008 Waves Modules, DHI (Danish Hydraulic Institute). Different aspects of BW engineering are highly elaborate – I will briefly focus on some selected portions of them in simple terms. An overview of civil engineering works on our seashore (see Civil Engineering on our Seashore), and of barrier systems engineering (see Flood Barrier Systems) were posted earlier – that laid out some basics of coastal engineering (CE) works. . . . 1. Breakwater Intro A BW generally refers to an in-water self-standing coastal protection or defense structure – shore-attached, detached or offshore. It belongs to the Water Barrier group of structures (see Flood Barrier Systems) in coastal engineering; and may define a system when multiple BWs and functions are integrated together as a package. The purpose of a BW is to diffract, break and obstruct the continuity of an incoming wave – in order to create a tranquil or shadow zone of minimal or no wave activities behind it. Although the term is primarily applied to describe coastal protection or defense structures against wave attack, the underlying concept is similar – for example, in breaking the flow of a river current to protect an inland harbor or river bank erosion from current forcing (collectively known as river training structures). The functional properties of a BW are achieved by designing a suitable layout and dimension – the size of which falls into the definition of a large structure – with its dimension, D scaling with the local wave length, L such that D/L > 1/5 (see Wave Forces on Slender Structures). This means that a BW has a significant presence in the surrounding hydrodynamic field – in diffraction, deflection, reflection, transmission, absorption and scattering of waves, currents and alluvial sediment transports and dispersion. One important aspect of BW configuration – in terms of hydrodynamic loading – is the convergence and divergence of wave energies. The convergence – in particular, at the convex bends and at BW heads – implies that those places must be stronger than the rest of the structure to withstand amplified wave loading. . . . 2. Breakwater Types and Functions The necessity for a minimal wave zone can be varied – in port applications, the purpose is to create a harbor where vessels and ships (see Ship Motion and Mooring Restraints) can safely navigate in and out – and moor to load and unload cargoes and people. The second most important necessity is to protect a shore from wave erosion and beach degradation, or to prevent entry of unwanted sediments into a harbor. BWs are classified as two basic types: Floating and Fixed. Floating BWs are pontoons tethered in position either by guide piles, or by chains anchored to the seafloor. A pontoon acts as a deterrent of, or as a low-pass filter to the incident waves (mostly short-periods ~ 4 s) – with the additional use as a loading/unloading platform. They are mostly applied in low wave-climate areas to design marinas where small pleasure boats can be safely secured on several inside finger floats. Different aspects of this type of BW – incident wave attenuation efficiency and transmission are discussed in the Wave Structure Interactions & Scour piece. The primary focus of this piece is Fixed BW. Breakwaters anchored to and founded on the seabed – as statically or dynamically stable hydraulic structure define a fixed BW. Depending on the scale of project and purpose, as well as on the prevailing hydrodynamic and wave climate, a fixed BW structure can be built by sheet pile walls, caissons (a concrete box or boxes filled with sand), rubble mounds, or combinations of them. Typically, caisson breakwaters can be a vertical face type, a composite type when the caisson sits on top of a raised platform built by rocks/rubbles, a perforated vertical face type (perforations eliminate wave reflection from the vertical wall), and armored caisson type (the seaside of the caisson is protected by rock armor units). Both sheet pile and caisson structures need quarry rock scour protection at seabed. . . . 2.1 Fixed Breakwater Fixed BW can be classified according to the magnitude of a Stability Number – defined as a ratio of wave height (H) to the product of armor unit relative density (Δ) and a characteristic dimension (D) of the unit or N_s = H/ΔD. When N_s ≤ 1, it falls into the category of a statically stable monolithic massive defense structure such as caissons and seawalls (in this case D is the height or width of the structure). All other structures including the rubble mounds and the shoreline itself are mostly dynamically stable with N_s > 1 (for rubble mounds, D = D_n50, the 50th percentile nominal rock diameter). In a dynamically stable structure, hydrodynamic forcing is assumed to cause profile changes in various degrees – with the displacements of rocks from a relatively unstable position to new stability. While this process goes on, the integrity of the structure remain largely unaffected or intact. However such structures succumb to failure – when large amounts of armor rocks are broken or are carried away exposing the underlayers and foundational core. BWs can be designated into four vertical zones according to their exposure to the hydrodynamic loading. They are: the Zone I – the bottom foundational zone below the level of Mean Low Water (MLW); the Zone II – the tidal zone from MLW to the Mean High Water (MHW), loading on this zone is very frequent and determines the longterm structural stability; the Zone III – the higher high water zone from MHW to the design level, wave attack on this zone is less frequent but of high impact; and the top Zone IV subjected to the effects of runup and overtopping. Shore perpendicular breakwaters attached to the shore are mostly conceived to serve beach management purposes. They are termed as Groins or Groin Systems, and have a range of typical shapes (Straight, T, Y, L, etc.) – the selection of which depend on the purpose and effectiveness. These types of breakwaters interrupt littoral transport, and attenuate the effects of onshore waves. They are usually low crested and are constructed of low-cost quarry rocks and runs. Literature and manuals suggest different planning approaches of such structures. For Groin Systems, the length of each unit is usually transitioned from short at the updrift side to the full length at the downdrift side. The spacing between each Groin usually scales with the length: the spacing is some 2 to 3 times the Groin length. Shore parallel detached breakwaters – as a way to manage beach erosion and littoral transport – are often identified according to its location with respect to the shoreline. A parameter (L) defining a ratio of breakwater distance from the shoreline (X_off), and the 80% of surf zone width (S_80, note that about 80% of littoral transport occurs within the surf zone; see The Surf Zone processes), or L = X_off/S_80. When L ≤ 0.5, the breakwater is classified as a Beach BW (it protects the foreshore without significantly altering the littoral transport). A Coastal BW is defined when 0.5 < L ≤ 2.0 (intervenes the littoral transport to prevent beach erosion). At L > 2.0, it is known as Offshore BW. This type must be highly robust to withstand high waves and to interrupt and diffract incoming waves. A fixed BW can also be classified according to the elevation of its crest from the still water level. In broad terms, two types can be identified: the emergent and the low crested breakwaters (LCB). The crest height of an emergent BW is usually high to prevent overtopping or to allow limited spray (breaking waves spray out into air) overtopping – and must take account of design storm surge height, wave set-up, wave run-up, height to compensate BW settlement and a freeboard on top of the design water level. If installed, the concrete cap of an emergent BW (usually used for utilitarian purposes) must be protected against overtopping damages by providing a crown wall. LCBs have various forms and heights depending on the desired limitations of overtopping – and the requirement to achieve certain wave attenuation goals. There are those that allow green overtopping (submerged BW acts as a weir transmitting a portion of the wave energy), and those that emerge and marginally submerge depending on the water level – thus allowing different categories of overtopping. . . . 3. Diffracting Waves by Configuring the BW Layout Diffraction is a process of bending the wave energy by obstructing its direct or head-on propagation. Waves lose a portion or all of its energy while bending from the illuminating zone to the shadows. Engineers use this property of wave behavior to design an area of low-energy wave environment so that vessels and ships can moor safely to load/unload cargoes and people – or to protect a shoreline from high energy wave actions and erosions. The ratio of diffracted (Hd) and incident (Hi) wave heights defines the diffraction coefficient, Cd = Hd/Hi. Characterization of the incident hydrodynamic field in quantitative terms must begin with a clear qualitative understanding of the wave and sediment climate systems of the area. The a-group and b-group of activities shown in the coastal engineering envelope (see Civil Engineering on our Seashore) are the ones to start with. They include: use of longterm timeseries measurements from moored buoy or other platforms (in absence of such measurements, Wave Hindcasting techniques are used, if necessary based on Beaufort Wind Scale) together with analytical and physical and/or numerical modeling. Before the times of digital computation and numerical modeling, engineers used diffraction diagrams and analytical models to determine diffracted wave heights. The Weigel (RL Weigel 1962) diffraction diagrams included in the SPMs and CEMs, and simple analytical models (Goda and others) are some examples. A simple illustration using the Goda relation, would show that an illuminating (a) 3-m, 8-sec head-on wave at 10-m water depth, would diffract to 0.34 m (Cd = 0.112) in the shadow zone at –60 deg (the direction refers to the direction of wave orthogonal approach). Modeling activities search for an optimal layout that would diffract the incoming waves to a tolerable height or energy level behind the BW. Physical scale modeling is somewhat a thing of the past as it involves considerable efforts and cost (however massive projects often require it). In contrast, modern practices of optimizing the configuration of a BW layout mostly rely on numerical modeling. First, the regional wave climate is established by wave action modeling – that lays out the boundary conditions for the detailed modeling including the outlines for most probable forcing scenarios. The most effective way of detailed layout optimization is by Mild Slope or Boussinesq (French mathematician and physicist Joseph Valentin Boussinesq; 1842 – 1929) wave modeling – an example of such an application is shown in the attached image. I love the beauty of Boussinesq modeling approach – its phase-resolving capability to analyze the non-linear wave fields close to the shore, etc. I had the opportunity to use it in multiple occasions – the results of one such application are published in my Ports 2013 Conference paper. While the capabilities are real – there are also many limitations and constraints of what a numerical model can or cannot do – therefore one should be careful in interpretations of model results, and their uncertainties. Some aspects of these issues are outlined in the Water Modeling piece. For the sake of brevity, the rest of this piece will primarily focus on rubble mound BW and designing armor rock size. . . . 4. Rubble Mound Breakwaters Rubble mound breakwaters represent a triangular (trapezoidal to be exact with thick peak) prism with its base at the seabed and its triangular peak rising to a certain height above or below the still water level (SWL). The thickness of the peak is structurally required to have the dimension of 3 armor rock sizes, often equipped with a concrete cap and a seaside crown wall for an emergent BW. The advantage of a rubble mound is its capacity to absorb and dissipate the wave breaking energy – the dissipation is ensured by the porosity of armor layer. It is a relatively cost-effective simple structure with the sides laid out in symmetric or asymmetric slope configuration. The slopes must be flatter than the rock angle of repose or internal friction (~ 1V:1.25H). In the case of an asymmetric triangle, the seaward side slope is usually flatter than the harbor side. Let us attempt to see some aspects of this structure in simple terms. Stability of an Armor Unit. The crucial step in BW engineering is to address the stability of armor rocks or concrete units placed (randomly by dumping, or one-by-one in regular orders) on the rubble mound slope. The hydrodynamic loading of a breaking wave must be balanced by the armor unit weight resting on a slope and held in place by neighboring units and the foundational core. The loading is primarily caused by breaking wave drag and lift forces (inertial forces are negligible, see Wave Forces on Slender Structures). These forces translate to the wave height when breaking water particle velocities become a square root function of H (see Tsunami and Tsunami Forces). In essence, the dynamic stability of armor units depends on a multitude of factors – related to (a) Wave Forcing, (b) Rock Properties and (c) Structural Integrity. They are:
. . . 4.1 Hudson Formula (RY Hudson 1958) The next breakthrough came from flume tests in the CERC lab facilities at Vicksburg, Mississippi. The derived relation, promoted by SPM manuals and has been in use for long time was the Hudson formula. It simply related N_s to the product of a stability coefficient and slope factor. The formula is based on flume tests relying on the actions of broken waves on non-overtopped permeable core BW slope. SPM manuals prescribed different applicabilities of this formula and provided different tabulated values of the stability coefficient. Although the formula was derived using regular waves, the manual prescribed to use significant wave height (Hs) in the 1977 manual – and changed it to the 10th percentile significant wave height (1.27Hs) in the 1984 manual and in subsequent CEM editions. The limitations of this simple formula are often cited as: (1) probable scale-effects from small model tests; (2) use of regular wave loading only during testing; (3) the effects of wave period and storm duration not accounted for; (4) damage level is not well-defined; and (5) primarily meant for non-overtopped permeable core structure. However, to ensure wide applicability, all these limitations (as we shall see except the wave-period effect) are accounted for, and lumped into the stability coefficient. The example (a) broken wave, when acts on a 1V:2H BW slope, the 1977 formula yield a rough quarry rock armor unit mass of 4.5 tonne with no damage. It nearly doubles to 9.2 tonne when the 1984 formula is used. . . . 4.2 Van der Meer Formula (JW Van der Meer 1988) Van der Meer (VDM) for his PhD thesis conducted elaborate lab tests in the Delta Flume. His derived formula is more complex than Hudson’s. And N_s is related to additional factors – by taking into account of the effect of wave period, wave breaking type, permeability, damage level, and storm duration. VDM formula is tested for wave steepness from 0.005 to 0.06, and with the maximum wave numbers of 7500, at which the forces on the armor unit reach equilibrium (meaning that no more damages could occur with further increase in the number of waves). Let us see how the VDM formula predicts rough quarry rock armor size for the example wave. The (a) wave breaks on the 1V:2H BW slope as a plunging breaker (see The Surf Zone). For 4000 waves on an impermeable core with no damage, the required VDM unit mass is 6.7 tonne (note that this size is smaller than what is required by the 1984 Hudson). If the wave period is increased to (b) 12-sec, the wave breaking type is still plunging, but then the mass increases to 12.7 tonne. For this particular wave forcing, it turns out that the Hudson 1984 formula is conservative for wave periods ≤ 9.7 sec. For heavy storms characterized by long period waves, the VDM formula is appropriate. . . . 4.3 Materials and Other Aspects As an alternative to quarry rock, engineers resorted to lab testing to develop different interlocking shapes of concrete units. In most cases, investigations leading to finding such units became necessary when suitable sizes of quarry rocks (most commonly used densities: rock 2.65 tonne/m^3; water 1.025 tonne/m^3; 1 tonne = 1000 kg) could not be identified and found for high wave climate areas – in cost-effectiveness, quantities, qualities and energy dissipation. Concrete units allow engineers to design steep slope (~ 1V:1.5H) rubble mounds, thus affording significant cost savings in relatively deep waters. The units are usually reinforced when the required mass of each unit is heavier than about 10 to 20 tonne (often constrained by the placing equipments and methods). Many countries have developed their own tested shapes, some common examples include (with the year and the countries of development): Tetrapod (France 1950), Tribar (USA 1958), Stabit (UK 1961), Tripod (the Netherlands 1962), Dolos (Republic of South Africa 1963), Seabee (Australia 1978), Accropode (France 1980), Shed (UK 1982), Core-loc (USA 1996), and Xbloc (the Netherlands 2003). I like to stop at this by noting many other aspects of rubble mound BW engineering that accompany design specs. In brief they include:
There we have it. Perhaps some moments of thoughtful reflection and reckoning from all of us are useful – on something as miniscule as a microbe virus yet powerful enough to shatter the confidence in our protective capability of public health. And on something – that opened a terrible flaw in otherwise assumed as civilized systems and norms – but which in reality were nothing but artificial covers on the hidden wounds inflicted by many years of skewed socioeconomic policies promoting asymmetry and inequity. On top of that climate warming is heading towards unsustainable instabilities and trends; and information abuses and malicious internet viruses are at an alarming stage of threatening public security and privacy. With all these, it is no surprise to hear global calls – loud and clear, for the strengths of wisdom, mutual respect and unity. . . . With that, let me finish this piece with a Koan: Nothing compares with the fury of jealousy, arrogance, anger and hatred – when built within the systems of power or is tolerated – it unleashes the ruthless monster of cruelty and brutality that burns everything it comes close to. . . . . . - by Dr. Dilip K. Barua, 19 June 2020 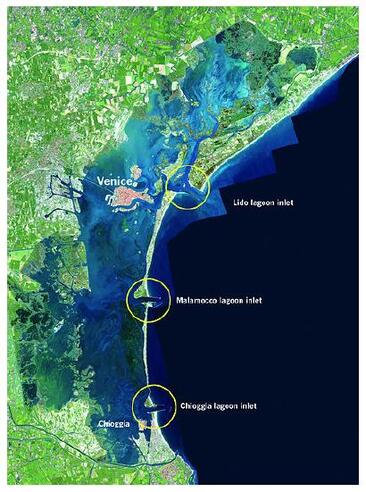 In an earlier piece, Civil Engineering on our Seashore, I have presented and broadly outlined the Coastal Engineering Envelope where several civil engineering measures were shown – that cater to the needs for protecting and developing the seashore. A brief of some 24 different kinds of coastal and port hydraulic structures were listed there. On this piece let us attempt to learn about the Storm Surge Barrier – but in a wider context of Flood Barrier Systems. The barriers as a way of managing water and floods – have two basic engineering components. The first is the dike on low lands, connected to the second component – the gated stream/river/estuary/waterway closure structures. The works represent a system that accounts for many engineering challenges – hydraulic, structural, geotechnical, and risk assessment – as well as impacts on the ambient environment defined by local Fluid, Solid and Life systems (see e.g. Environmental Controls and Functions of a River). In the back drop of Warming Climate with consequent Sea Level Rise, flood barrier systems are becoming increasingly relevant – as one of the management Strategies to cope with the threatening rising sea, and increasingly frequent and intense storm surge.
This piece is built upon materials gleaned from several sources and websites. Unless specified otherwise, they include the following. On river floods: Hydraulic Design of Flood Control Channels, USACE EM 1110-2-1601; Hydrologic Frequency Analysis, USACE EM 1110-2-1415; and Design and Construction of Levees, USACE EM 1110-2-1913. On coastal flood/storm surge: Storm Surge Analysis and Design Water Level Determinations, USACE EM 1110-2-1412; Hurricane and Storm Damage Risk Reduction System Design Guidelines, USACE; and TUDelft (VSSD) Breakwater and Closure Dams (2008, 2nd ed). . . . 1. Flood Barrier Systems and Issues Before jumping on to discussing the flood barrier systems – perhaps it would be instructive to begin by introducing the Water Barrier concept in a broader context. Because all barriers under this generic term, and in the capacities of a hydraulic structure – have one common purpose – that is to protect an area from the onslaught of water actions. These protections can simply be sorted out against the actions of:
Wave and Current Forces, Agitations, Erosions and Scours: (1) emergent and submerged fixed breakwater; (2) floating breakwater; (3) sill, reef or weir catered to gradually weaken water forces; (4) beach nourishment; (5) a buffer zone of hardy and water tolerant plantations to reduce forces; (6) groin; (7) jetty and training wall to deflect forces; and (8) seawall, bulkhead and revetment; and (8) stone ripraps on banks and beds. Inundation and Runup by Propagating Flood Waves: (1) on banks or shorelines – stone ripraps, earthen dike or monolithic vertical flood wall with channel closures and sluice outlets; (2) purposely built sand dune; (3) isolating an area to create polders by ring, or partial-enclosure dikes or flood walls with channel closures and sluice outlets; (4) gated barrier on streams, rivers, estuaries and river mouths – designed for actuation in times of unwanted high waters caused by flood waves of all sorts – tide, storm surge and tsunami; (5) managing channel networks through diversion barrages, closure dams and dikes; (6) the crucial step of implementing closure dams; and (7) pumping stations to augment drainage relief of the protected area. Sedimentation Management: (1) sluice outlet to drain out water and accumulated sediments, together with gates to prevent entry of sediment-laden high-stage water into the protected area; (2) sediment trap dug into channels to be dredged occasionally; (3) updrift to downdrift sediment by-pass to balance accretion-erosion; (4) updrift breakwater to trap sand, and prevent channel sedimentation by breaking the continuity of littoral drift; and (5) occasional dredging of silted basins and channels. Effects Assessment: It is customary that all modern engineering measures must accompany an assessment of their effects on the Fluid, Solid and Life Systems – with clear identifications of impacted areas on the surrounding – both in short and longterm perspectives. But, many engineering measures failed to take proper account of effects and remedies. The 2012 USGS report (C1375): A Brief History and Summary of the Effects of River Engineering and Dams on the Mississippi River System and Delta – outlined in vivid terms some effects of river engineering and protection works – that totally changed the character and regime of a river – adversely affecting its living dynamic equilibrium process of sustenance. Many such works have been (perhaps even being) installed around the world – without due diligence of assessing their effects and impacts – thus weighing their pros-and-cons on the interdependent Fluid-Solid-Life systems. Risk Assessment: Flood barrier systems are a costly investment tasked to protect areas, properties and lives against extreme hydraulic events and forces that have the overwhelming power of destruction. Therefore it is a compelling necessity to complete a risk assessment procedure with due diligence and earnest. The 2012 NAP publication #13393 – Dam and Levee Safety and Community Resilience: A Vision for Future Practice – discusses some of the Flood Barrier safety and risk mitigation issues, and community involvements. Risks and safety standards are usually described by coining different acronyms. New acronyms appear as emphasis shifts or as new thinking emerges. They result from the underlying realization that risk is not something that can be eliminated – but rather can be minimized. As discussed in the Uncertainty and Risk Article – risk quantification is a product of the uncertainty associated with the forcing functions – and both the short and long-term consequences or damaging actions of that force. It requires addressing a question – how to define a certain Safe Tolerable Threshold (STT) during the minimization processes. In the context of the collapse of Flood Barrier Systems – the STT definition and risk characterization mean finding an acceptable damage threshold that would ensure safety of lives and properties. When defining standards in one way or another – the aim is to arrive at risk as low as possible – or safety is as high as possible. Both the approaches are definable in probability scales. As can be understood, the rationality of finding a satisfactory cost-benefit ratio underlines all STT definitions. But, then there is no uniquely acceptable definition across the board – therefore disputes, court-cases and legal definitions and re-definitions come into the picture. Aspects of this are also shared in an ASCE Collaborate Discussion. With this brief layout of water barriers, let us move on to discussing the specific issues of flood barriers. Among the many measures identified above, the ones belonging to the group described in 2 are the focus of this piece. Let me first briefly elaborate some key hydraulic basics of this group – then move on to outline some major Storm Surge Barriers – with detailing out some aspects of the Venice MOSE project (image credit: anon). . . . 2. Flood Barrier Hydraulics It is necessary to comprehend some key hydraulic technical issues – that are important in aspects of planning, designing, construction, and functions. In all these aspects, different methods and practices are implemented in ways – how a barrier handles the potential and kinetic energies – in eliminating, reducing or modulating their power. Let us attempt to see them. In barriers installed to prevent flooding due to inundation and runup – potential energy is gradually elevated as the hydraulic head difference increases between the two sides of a barrier. One knows too well that the forces caused by the difference – exerted on an earthen dike, a vertical monolithic wall, or a gated barrier structure – are what cause failures (see Civil Engineering on our Seashore). The threats to their stability and integrity take different dimensions and can be translated into: The first hydraulic issue that comes to one’s mind – is the selection of an upper-envelope extreme event up to which a given barrier system can be designed to withstand and provide protection. Methods and issues related to defining such an event have been discussed in two pieces posted earlier – Uncertainty and Risk; and The World of Numbers and Chances. Among the two modes for flooding, inundation is like the gradual encroachment by a carpet of water with concentration of currents when the dispersing flood-wave faces resistance. In contrast to this, broken-wave runups are forceful in actions with impacts on structures and bed. A standing pressure force develops on the water retaining side of the structure. This pressure representing potential energy causes very high kinetic energy when released (e.g. a 1 m of head difference could generate a flow velocity as high as 4.5 m/s). There are also some dynamic elements to the pressure field – induced by propagating disturbances and/or by surface waves. These forces apply an overturning moment on a vertical wall, and cause pore pressure on an earthen dike. Earthen dikes are designed to minimize the effects of pore water pressure. At a certain moment when the freeboard is less than some tolerable limits, the potentials of overtopping and eventual failure emerge – in particular in the regions of weaknesses. In such cases, the power of concentrated flows continues to erode and topple the barrier until the forces diminish, and the hydraulic head difference between the two sides is levelled off. A vertical wall causes some reflections of the dynamic pressure and surface waves. A sloped earthen dike, on the other hand is dissipative by nature. Areas enclosed by dikes require a drainage sluice outlet gated structure. Most often a flap gate proves to be a very cost-effective alternative. It is a simple structure with gates hinged at the top while the bottom part can flap outward – to let the draining out of accumulated water from inside the protected area. The gates are designed not to flap inward to prevent entry of water from outside. To cope with adverse drainage-gradients (that often happen at very high tide, but most notably during storm tide when receiving basin water level is higher than the protected area), pumping stations are installed at the drainage outlet structure to pump out accumulated water from inside the protected area. . . . 2.1 Closure Dams In many flood barrier engineering – a closure dam is required to close the original channel to let the flow divert toward the newly-installed gated-structure. For a uni-directional flow, closing of the original river course is easily done after diversion. For tidal channels, an intensive sequence of activities is required to close the final water-gap. This is mostly accomplished during a short window of neap-tidal slack water. Purposely-built middle islands – together with well-mobilized equipment and workforce are employed to close the gap at one go. While the closing operations continue, the peripheral parts of the dam are protected simultaneously by dumping rocks. I had the opportunity to learn about different aspects of closure dam hydraulic engineering while studying at Delft – working on a group thesis on Asan Bay closure dam in Korea. Also, had the opportunity to be present and witness the labor-intensive works of Feni River Closure Dam in Bangladesh. More on closure dams are available at: TU-Delft 2008, Breakwaters and Closure Dams, 2nd edition; CIRIA Rock Manual 2006, Design of Closure Works (Ch 7). In my 1993 paper {Practices, Possibilities and Impacts of Land Reclamation Activities in the Coastal Areas of Bangladesh. In: Grifman PM and Fawcett JA (Eds), International Perspectives on Coastal Ocean Space Utilization, University of Southern California Sea Grant Publication, pp. 343-356} traditional practices of building large-scale cross-dams or closure dams in Bangladesh were discussed. The 1956-57 Cross-dam 1 and the 1964 Cross-dam 2 – were implemented to close some dying branches of the Meghna Estuary, and some 52,000 ha of land was reclaimed. . . . 2.2 Other Hydraulic Aspects An important step in flood barrier engineering is to design and construct measures for preventing scour of channel bed. A bed scour is initiated and intensified, because installation of gate-housing structures reduces the channel cross-sectional area – thus increasing the flow velocity, and inducing scour-causing vortices around the gate structures (see Turbulence, and Wave Structure Interactions & Scour). Based on many years of experience, Dutch engineers developed methods and special equipment to place woven straw mattresses on the channel bed. Ballasted by rocks, the mattress acts as a filter to prevent escaping of bed sediments – as well as becomes the prepared foundation on which structures can be placed. This is unique, in a sense that many other methods rely on founding the gate-structure deep into the solid bed on which superstructures are built upon. Engineering of gates on barrier openings have many familiar forms: e.g. gates sliding against structure piers vertically; swing gates hinged to the bottom; swing gates hinged to the bank; rotating drum gates; inflatable gates; gates sliding horizontally; swing flap gates hinged to the top; etc. Some key considerations that lead to the choice of one or the other are: convenience of recess structure for housing the gates when not in operation; strength of the gates and power required to operate them to withstand the design high hydraulic heads, etc. A very important effect of implementing storm surge barriers – is the reduction of tidal prism (see Managing Coastal Inlets). This happens because of the reduced cross-sectional area. Since the behavior of the Fluid (in this case Water) System is changed – the ambient characteristics of the Solid and Life Systems – dependent on water properties and circulation are affected. Therefore a thorough environmental effects assessment is imperative. . . . 3. Highlights of Some Major Storm Surge Barriers In the world of modern flood barrier engineering, the first one to occupy the history book is the 32 km long Afsluitdijk closure dam in the Netherlands completed in 1932. This dam separates the shallow IJsselmeer Lake from Wadden Sea. The primary purpose of this dam was to reclaim land from the lake. Starting from this great feat of hydraulic engineering, let me highlight some major storm surge barriers completed around the world. Delta Works, the Netherlands: These works refer to massive barriers, navigation locks and dikes – constructed to control and prevent storm surges entering through several branching delta estuaries of the Rhine-Meuse-Scheldt river system. The works were commissioned after the devastating storm surge flooding of 1953. The last one of the Delta Works was finished in 2010 together with environmental restoration works. The gates on the openings of the barriers vary in technical innovations from sliding to bank-hinged to inflatables. The only sea arm that remains open in the Netherlands is the Western Scheldt that leads to the Antwerp Maritime Port in Belgium. With the threat of rising sea, strengthening of existing structures is on the plan. Thames Barrier, London, England: The same 1953 North Sea storm surge that prompted Delta Works in the Netherlands – was also the reason for initiating the Thames Barrier. Commissioned in 1984, the purpose of the barrier system comprising of the dikes – was to protect low lands of the greater London area from the North Sea high tide and storm surge propagating through Thames Estuary. It was built on the 520 m wide estuary by dividing it in 4 basic segments and 2 navigational spans. The barrier structure openings are equipped with rotating steel drum gates that rest on the channel bed when sleeping, and are rotated to rise in the event of unacceptable forecasts of high tide or storm surge. IHNC Storm Surge Barrier, USA: This barrier (Inner Harbor Navigation Canal) was constructed by US Army Corps of Engineers near New Orleans on the confluence of Gulf Intracoastal Waterway and Mississippi River Gulf Outlet in 2013. The purpose of the barrier was to protect some of the low lying vulnerable areas of greater New Orleans against storm surges from the Gulf of Mexico and Lake Borgne. The barrier system consists of flood walls, bypasses, navigation locks and gated barriers. To reduce the risk of flooding in the greater New Orleans area - a massive $14 billion project - the Hurricane and Storm Damage Risk Reduction System (HSDRRS) is being built by USACE with supports from local and outside consultants. The system is scheduled to be completed in 2023. A recent discussion throws further light on the New Orleans Barrier system. Saint Petersburg Dam Complex, Russia: The Saint Petersburg Flood Prevention Facility Complex is a 25 km barrier system – completed in 2011 to protect Saint Petersburg against storm surge coming from the Gulf of Finland. Saint Petersburg is founded on low marshy lands located in Neva Bay – and has seen the onslaught of some 340 devastating floods in the past. The system also forms part of the dike ring road that passes through the gated barrier structure as underwater roadway tunnels. It includes some 30 water purification units designed to maintain the water of Neva Bay healthy. Among many others in the planning process – a massive storm surge barrier (New York Harbor Storm Surge Barrier) is planned to protect the Lower New York Bay from the onslaught of storm surge coming from the Atlantic through the Outer Harbor. . . . 3.1 MOSE Project Venice, Italy Let me begin with a little bit history. Venice marshy islands started to get settled by refugees when they fled from barbarian attacks in the 5th century CE. It gradually became important and powerful as a maritime port and harbor. Venice lagoon gradually silted up by sediments brought in by 3 rivers. At sometime later, the river outfalls were diverted away from the lagoon to prevent sedimentation. In the 20th century, many wells were dug in Venice to extract water for agriculture and industry use. The extraction induced more subsidence of the marshy lands – and was banned only in the 1960s. Present subsidence rate of Venice is about 1 – 2 mm/year. Long waves such as tide, storm surge and tsunami are subjected to transformation as they propagate from open water to constricted areas (see Transformation of Waves) – in the process waves are amplified and distorted. Similar process happens, as the low Mediterranean tide gets amplified as it enters Adriatic Sea to Venice. As an example, in January 2020, a 30 cm tide at Catania, Sicily amplifies to 100 cm at Malamocco, Venice. A term known locally as acqua alta is used to refer to tidal flooding of the Venice city center – tide reaching to + 0.8 above local datum. The analyses of 1872 – 2006 tide records show that acqua alta mostly occurs in the months from October to December due to both astronomical and meteorological phenomena. Since about 1950s, the frequency and intensity of acqua alta have been registering high, due to subsidence as well as the rising sea level of the Adriatic. When tide is + 140 cm, about 90% of Venice is flooded. Low level flooding during high tide are becoming more common – presumably due to rising sea and subsidence. In the backdrop of all these, the MOSE (Modulo Sperimentale Elettromeccanico) flood barrier project was conceived in 2001 and construction began in 2003. It consists of 78 independently moving closure gate elements at 3 inlets (18 at Chioggia; 19 at Malamocco; 20 at Lido-Treporti and 21 at Lido-S. Nicolo). These 3 inlets are located on the barrier island chain that separates Venice Lagoon from the head of Adriatic Sea. The purpose of the project is unique – in a sense that unlike many other major storm surge barrier projects around the world – it is planned to operate rather regularly to lessen the effects of high tides and storm surges penetrating into the Venice lagoon. The rectangular gate elements were designed to rest on seabed recess structure when not active. The resting is ensured by filling the elements with water. Activation of the elements is initiated when the tide is forecasted to reach +110 cm. The elements are raised from their recesses by pumping compressed air into the elements to drain out water. The anticipated completion timeline of the project is 2022. Among the 3 inlets, the Malamocco Inlet is designed to accommodate marine traffic to the Venice Port during the inlet closures. Differences of opinion appeared about the adverse effects of closures – in terms of harming ecology, of very high cost, and of doubts about the effectiveness of the inlet structures. Additionally, concerns were expressed about navigational delays and the cost for such delays on transportation. A recent discussion indicates the high frequency of rising seas and how the barrier system is equipped to cope with that. . . . It has been a great pleasure writing this piece. Let me finish it with a little Koan: Why let it wither away, some water-of-life on the plant would have worked to let it stand upright and unfold the fragrance of flower. . . . . . - by Dr. Dilip K. Barua, 26 January 2020  This piece is about the varieties of Coastal Civil Engineering (CCE) works we all see – when visiting seafront to relax, to feel the warmth of ocean in continuous pounding of waves, or when seeing vessels navigating in and out of ports and harbors. These works result from engineering efforts that have three well-known tenets of civil engineering: coastal hydraulic engineering (or simply Coastal Engineering), coastal structural engineering and geotechnical engineering (structural and geotechnical are often lumped together as structures engineering). Coastal hydraulic engineering term is sort of a misnomer – because it not only covers analysis, modeling and determination of hydrodynamic forces caused by water, water level rise and fall, current, wave and bed-level changes – but also includes similar activities due to wind forcing. The combined effects caused by wind and water are known as metocean processes and forces.
Before moving further it is important to build into our concept the extent of geographical area where civil engineering is referred to as CCE (to avoid confusion, CE is reserved to denote Civil Engineering). This area termed as the coastal zone – extends from the inland topographical limit reached by major storm surges and tsunamis to the continental shelf break. Continental shelf mostly of turquoise water, having an average bottom slope of some 1V:100H extends from the shoreline to a seaward line where the slope abruptly dips down into the ocean at about 1V:40H or steeper. This line begins roughly in the region where waves of about ≥ 10 seconds will start feeling the bottom – consequently being subjected to the transformative processes of refraction and shoaling (see Wave Transformation piece on this page). Generally, mariners call the blue ocean beyond continental shelf – high seas. The definitions of inland limit vary among countries – and depend on several criteria such as: technical, legal, administrative, disaster management and hazard insurance – but they all invariably include coastal waterways, river mouths, estuaries and bays. I have discussed many aspects of CCE in different pieces on the NATURE and SCIENCE & TECHNOLOGY (S & T) pages. Thought a piece of introductory nature will complement those. . . . 1. Coastal Boundary Definitions In the US Submerged Land Act (1953) a coastline is defined as: the line of ordinary low water along that portion of the coast which is in direct contact with the open sea and the line marking the seaward limit of inland waters. The same Act defines coastal submerged land under the jurisdiction of coastal States as: navigable waters, and lands beneath, within the boundaries of the respective coastal states out to 3 nautical miles from its coastline. The Outer Continental Shelf Lands Act (OCSLA 1953) defines federal jurisdiction on coastal oceans as: all submerged lands lying seaward of state submerged lands and waters (e.g. outside shelf lands seaward of 3 nautical miles). Perhaps it is useful to add a brief on the legal definition of Maritime Boundary. Part of this brief is based on my 1994 IEB paper: On the Formulation of Coastal Zone Management Plan for Bangladesh. The following definitions of the boundaries are agreed upon by signatory countries (including the land-locked countries which are given the right to claim maritime transport access through their coastal neighbor) at the UN Convention on the Law of the Sea (UNCLOS 1987). It was developed and refined within the framework of the UN – during a period from 1970 to 1984.
. . . 2. Engineering, Civil Engineering and Coastal Engineering There are other names addressing the same problems of CCE but focusing on some particular aspects: like port and harbor engineering, maritime engineering (coined first in European literature), and marine engineering. The last term is loosely applied in civil engineering to describe in-water works – but its root mainly lies in describing mechanical-electrical engineering, navigation and naval architectural aspects of seafaring vessels. Ocean engineering, oceanographical engineering and offshore engineering terms are also used to describe works in coastal and deep waters. Offshore engineering term is primarily applied to describe isolated in-water works in deep water – like oil terminals and marine pipelines. There are many definitions of CCE – different in wording but common in contents. Let us attempt to define it in this piece as: CCE refers to the practice of planning, designing and effects assessment of civil engineering works for the protection and preservation of, and developments (water-front townships and cities, recreation, marine transports and installations, and value-adding improvements) within the coastal zone. The history of CCE is briefly discussed in the Resistance to Flow on this page – it is a fairly new discipline – the official recognition and definition was launched only about 70 years ago – at the First Conference on Coastal Engineering held in Long Beach, California in 1950. Coming back to the definition – one can see that it relies on the understandings of two other terms: civil engineering, and engineering. There are many definitions of these two terms in literature, but I prefer using the following two. According to The National Academy of Engineering and National Research Council: engineering is the study and practice of designing artefacts and processes under the constraints of the laws of nature or science and time, money, available materials, ergonomics (it is the process of designing or arranging workplaces, products and systems to satisfy the needs of people who use them) environmental regulations, manufacturability, and repairability. In NAP #12635 Publication the following texts elucidate the understanding of engineering practices in a very detailed and useful manner (I have rearranged the lines somewhat for clarity). Engineering “habits of mind” (refer to the values, attitudes, and thinking skills associated with engineering; AAAS 1990) align with what many believe are essential skills for citizens in the 21st century. These include: (1) Systems Thinking: systems thinking equips students to recognize essential interconnections in the technological world and to appreciate that systems may have unexpected effects that cannot be predicted from the behavior of individual subsystems; (2) Creativity: creativity is inherent in the engineering design process; (3) Optimism: optimism reflects a world view in which possibilities and opportunities can be found in every challenge and an understanding that every technology can be improved. Engineering is a “team sport”; (4) Collaboration: collaboration leverages the perspectives, knowledge, and capabilities of team members to address a design challenge; (5) Communication: communication is essential to effective collaboration, to understanding the particular wants and needs of a “customer,” and to explaining and justifying the final design solution; and (6) Attention to Ethical Considerations: ethical considerations draw attention to the impacts of engineering on people and the environment; ethical considerations include possible unintended consequences. The 2008 ASCE BOK2 (Civil Engineering Body of Knowledge for the 21st Century, 2nd ed.) defines and elaborates civil engineering as: the profession in which a knowledge of the mathematical and physical sciences gained by study, experience, and practice is applied with judgment to develop ways to utilize, economically, the materials and forces of nature for the progressive well-being of humanity in creating, improving and protecting the environment, in providing the facilities for community living, industry and transportation, and in providing structures for the use of humanity. All these definitions are quite lengthy, but they were developed to cover all different aspects – from scientific, technical, ethical-legal, and societal perspectives. I have written in the Creativity and Due Diligence piece that, CCE as a creative profession has the role . . . in the discipline of civil/hydraulic engineering, applied science provides the baseline knowledge on data and analysis, while technology provides tested products and materials. The role of an engineer is to find solutions to a given problem using resources from these two sources. To do it successfully, it is important for engineers to understand the necessary basics of the S & T. Failing in this matter affects the soundness of an engineer’s judgment. Therefore engineers are part of the S & T endeavors by being intricately involved in the development and progress – sometimes working at the forefront, but most often in the practical applications of science and technological advances to the real-world problems . . . And to accomplish that, engineers by and large, and perhaps more than any other profession – spend a significant portion of their time on computing to create acceptable, defensible and implementable solutions in quantitative terms – using slide rule in earlier times (until about 1970s) to the scientific calculators and personal computers in modern times. . . . 3. Coastal Engineering Envelope Perhaps it is helpful to enumerate some of the sub-disciplines commonly included in the coastal engineering envelope. The first group (a-group) of activities includes those – aimed at establishing critical planning and design conditions and criteria by envisioning the most probable operational and design loading scenarios, uncertainties and risks for various interventions/structures (these structures not only include hard measures of concrete, steel and stones; but also soft structures like beach nourishment and coastal vegetation/tree barriers) based on analysis and modeling of various environmental parameters. This group includes: (1a) hydrodynamics: water level, current, and wave; (2a) wind climate and storms; and (3a) sedimentary climate: coastal geology and sediment transport processes. The second group (b-group) of activities utilizes the first – for planning, designing and assessing the effects and risks of: (1b) coastal zone development and value adding; (2b) coast and shore preservation and protection; (3b) intakes and outfalls; (4b) dredging and spoil disposal; (5b) coastal waterfront and marine terminal structures, including marina; (6b) offshore and pipeline structures; and (7b) port and harbor developments and structures. I have included an image of the coastal envelope showing the discussed disciplines. As indicated earlier, Water Modeling is an integral part of CCE activities. . . . 4. Engineering Project Phases An engineering project starts with a very limited knowledge – starting from that, the project moves forward to develop criteria, conditions, specifications, etc. in distinct phases of activities. At the first of three phases – the Conceptual Phase (known as Pre-FEED {Front End Engineering and Design} in Oil and Gas Industries) – starting from scratch, problems are defined and the project is visualized, they are then translated into a complete solution package (analysis and design sketches, alternatives, economics, etc) – only at a high level by utilizing available regional and site-specific (mostly unavailable) information. This phase is usually preceded by very high level technical feasibility and economic viability studies. At the next phase – known as the Preliminary Phase (FEED in Oil and Gas Industries) – the conceptual package is critically reviewed, a site-specific information base is established by measurements and modeling, new alternatives are generated, and the conceptual package is revised and updated – but the issued design sketches and specifications are not yet ready for implementation. At the Final or Detailed Phase – a final critical review of the preliminary package is undertaken – updated and refined where necessary, usually no new alternatives are generated – construction, monitoring and supervision methodologies are laid out by detailing each nut & bolt – and the final design sketches and specifications are issued for implementation with the consultant having the additional task of selecting a contractor. The above phases are usually conducted by different engineering consulting firms for better accommodation of talents and ideas, but often the final phase is eliminated entirely for large projects – by combining the final design and construction into a single package. One prominent form of this system is known as the Engineering, Procurement and Construction or EPC method, where the contractor is responsible for the final design, procurement of materials, and delivering the finished functioning product to the client. To assist and oversee the EPC contractor activities – the project owner usually engages a specialist firm known as the Project Management Consultants (PMC). Apart from these, there are many other consulting, contracting and management terms used in different project phases and construction – and they are usually not the same across civil engineering projects – but vary according to types, even from one country to another. . . . 4.1 Design Criteria A little note on design criteria – they refer to the parameters that must be applied as a minimum for designing project elements; and mostly include: (1) environmental metocean forcing functions, (2) configuration and layout, (3) structural material strength, durability, etc (4) structure-geotechnical, (5) construction and construction foot-prints, (6) operation and maintenance, (7) economics, (8) safety and emergency access, (9) ergonomics, and (10) environmental effects. Some of these criteria are established by scientific and engineering analyses; others come from certified standards and codes; and client and regulatory requirements. Any lapses in not taking proper account of the above criteria constitute a failure. . . . 5. Outline of Some Typical Coastal Engineering Works Having clarified the meanings of different terms let us move on to the rest. Let me begin by listing some of the major works identified with coastal engineering. The list is long – I am tempted to provide a brief outline of some important works that are applied worldwide affording developments of manuals, standards and codes (see more in The Grammar of Industrialization):
On Science of Nature Page: Ocean Waves; Sea Level Rise - the Science; Coastal River Delta; Linear Waves; Nonlinear Waves; Spectral Waves; Turbulence; Coastal Water; The Hydraulics of Sediment Transport; Waves - Height, Period and Length; Warming Climate and Entropy; Characterizing Wave Asymmetry On Science & Technology Engineering Page: Common Sense Hydraulics; Uncertainty and Risk; Transformation of Waves; Resistance to Flow; Water Modeling; Sea Level Rise - the Consequences and Adaptation; Tsunami and Tsunami Forces; Storm Surge; The Surf Zone; Wave Forces on Slender Structures; Ship Motion and Mooring Restraints; Wave Structure Interactions & Scour; The World of Numbers and Chances; Managing Coastal Inlets; Propwash; Flood Barrier Systems; Breakwater; Harbor Sedimentation; Uncertainty Propagation in Wave Loadings; Force Fields in a Coastal System; Coastal Ocean Currents off Rivermouths; The Grammar of Industrialization - Standards, Codes and Manual; Coastal Water Level . . . 6. Characterizing Engineering Failures How does one characterize the failure of a structure – like the listed ones? Failures generally fall into 4 basic types: (a) environmental load failure (the cause for this failure is attributed to the exceedence or unexpected occurrence of design loads and loading conditions), (b) functional or ergonomic failure (although the structural integrity remains intact, the structure fails to provide its designed operations, functions or performance), (c) structural failure and (d) geotechnical failure. The last two could have the following 3 causes:
Here are few more relevant definitions taken from British Standard – BS 1990-2002, Basis of Structural Design 2010. design working life: assumed period for which a structure or part of it is to be used for its intended purpose with anticipated maintenance but without major repair being necessary . . . hazard: . . . an unusual and severe event, e.g. an abnormal action or environmental influence, insufficient strength or resistance, or excessive deviation from intended dimensions . . . limit states: states beyond which the structure no longer fulfils the relevant design criteria . . . ultimate limit states: states associated with collapse or with other similar forms of structural failure . . . serviceability limit states: states that correspond to conditions beyond which specified service requirements for a structure or structural member are no longer met . . . reliability: ability of a structure or a structural member to fulfil the specified requirements, including the design working life, for which it has been designed. Reliability is usually expressed in probabilistic terms. NOTE Reliability covers safety, serviceability and durability of a structure . . There are many more features of CCE, but for the sake of brevity, I like to stop at this, only to point out one very important aspect. Coastal structures are not like a tall building standing on a dry land – and they should not be treated as such. Because of their exposed location in water or at the water-front, they continuously come under attack by the dynamic and uncertain metocean forcing – from regular to extreme. They must withstand different aspects of the force fields - during construction and operational lifetime, as well as face the consequences of uncertain fluid-structure interaction processes, and have to cause minimum impacts on the surrounding environments. Therefore the role of a coastal engineer is very crucial – not only in the establishment of design and operational conditions and criteria, but also during the process of planning, design and construction. Lack of effective coordination, cooperation and concordance among various disciplines – or perhaps in not recognizing the proper roles required of certain disciplines – could lead to earning bad reputation, and to risks of incurring serious economic losses. . . . I like to finish this piece with some lines of poetry written by a seemingly unknown amateur poet, but the poem was made significant by Saint Mother Teresa (1910 – 1997; Nobel Peace Prize 1979; Bharat Ratna 1980; Sainthood 2016) who displayed it in her office. People are illogical, unreasonable and self-centered Love them anyway. . . . Give the world the best you have and you’ll get kicked in the teeth Give the world the best you have anyway. . . . What motivation went into such portrayals of the societies we live in – and the strength and courage the poet was asking for? One can hardly afford not to like the poem – but perhaps more so by a personality none other than Mother Teresa – because it tells all about her life and experience. . . . . . - by Dr. Dilip K. Barua, 5 February 2019  1. Propwash Inro
This topic is about the consequences of high turbulence and flow velocity that accompany a fixed-pitch screw propulsion ship. Propwash is the term used to describe the high exit velocity a propeller nozzle generates – and in the context of this piece – it is about the propwash effects on a marine terminal during the berthing and unberthing of a ship. The purpose of generating the high exit velocity by a ship is to cause equivalent forward thrust on it – with Newton’s (Isaac Newton, 1643 - 1727) Third Law of Motion in action. Screw propeller blades are twisted in such a way that a rotating propeller produces a high pressure difference by sucking in waters from one side and discharging them to the other to generate the exit velocity required to push a ship forward. The larger the DWT of a ship (see the Ship Motion and Mooring Restraints piece on this page for DWT) the higher is the requirement of propeller powers. But navy and coast guard vessels requiring high speeds, and Tugs tasked to haul barges or to maneuver large vessels during berthing and unberthing – however small they may be – also need to have high propeller powers. For navy and coast guard vessels – the high speed water-jet propulsion system is more of a requirement because the conventional screw propulsion system would just prove inadequate. Let me share some elements of this important port and maritime engineering topic in simple terms – focusing primarily on propwash and its effects. . . . 2. Propulsion System Thrust Let me begin by focusing on engine thrust that moves a ship ahead. In still ambient water, propeller-induced thrust depends on three important factors – the product of these three describes the efflux – the exiting flux of water from the propeller nozzle. The first is the density of water – which means that with other factors remaining constant – a ship will have somewhat higher thrust in salt water than in fresh water (in addition a ship will feel somewhat lighter in salt water due to enhanced buoyancy). The second most important parameter – is the diameter of the propeller Dp – the thrust is proportional to the square of Dp, implying that it will increase by 4-fold if Dp is changed, let us say, from 1 m to 2 m. Actually, this dependence comes from the equation of the area of a circle – the area being proportional to the square of the diameter. The concept is utilized by encasing the propeller in a duct or short nozzle to obtain more power for the same engine rpm. Despite the engine thrust being highly dependent on the propeller diameter, there is a limit to its maximum size. One of the reasons is that the diameter must scale with the draft of the ship – otherwise a portion of the propeller will surface and rotate in air. But such surfacing cannot be avoided when a ship rides on rough seas with high roll and pitch motions. . . . 2.1 Jet Exit Velocity To describe the third important factor – one needs to take the help of Bernoulli Equation (Daniel Bernoulli, 1700 – 1782). As often pointed out in other pieces, the flow-induced dynamic pressure illustrated by Bernoulli is very important in fluid mechanics – this pressure is proportional to the square of the velocity. Here again, if the velocity is increased, let us say, from 1 m/s to 2 m/s, with other factors remaining constant, the thrust will increase by 4-fold. The exit velocity of an open propeller behaves in a certain way. At a distance of about 0.5*Dp behind the propeller, the exiting jet from an unducted propeller becomes constricted to Do = 0.7*Dp. The maximum jet exit velocity Uo occurs at this location with dissipation taking place further behind. Unlike the other two factors (water density and propeller diameter) – one does not know the jet exit velocity a priori. How to estimate it? To answer this question engineers had to conduct series of lab experiments. Delft Hydraulics took the pioneering role in this regard with HG Blaauw and EJ van de Kaa publishing their paper in 1978 – with more subsequent researches coming from other institutions. Remarkable among these, is a review made by MJ Prosser in 1986. Other notable titles dealing with analysis and design recommendations include: EAU (1996); PIANC (1997, 2002 and 2015), Port Designer’s Handbook: Recommendations and Guidelines (CA Thoresen 2003), Design of Marine Facilities for the Berthing, Mooring and Repair of Vessels (JW Gaithwaite 2004), The Rock Manual (CIRIA 2006), HJ Verheij and C Stolker (2007), and K Römisch and E Schmidt (2009). The first theoretical foundations of the behavior of an expanding jet came from ML Albertson and others (1948) and N Rajaratnam (1976). However despite nearly seven decades of scientific research and engineering, one is tempted to say that propwash and its loading on structures and seabed, and interactions – remain inadequately understood. In the simplest of all the known empirical relations, the exit velocity Uo is described empirically as the product of propeller revolutions per second n, Dp and a thrust coefficient Kt. The dependence on the thrust coefficient is somewhat weak – but a higher pitch (pitch is the distance traveled by a propeller in one complete revolution in no slip condition. Propeller blades are twisted to have a constant pitch from the root at the hub to the tip. The forward travel of a ship is however less than the nominal pitch determined at 0.7*R, R being the propeller radius. The difference is known as the slip. A note on propeller blade numbers – high numbers are usually optimally chosen to minimize vibration and noise.) ensures a higher Kt. Inclusion of Kt makes things somewhat circular – but to go around that, a rough estimate is possible without using Kt – and investigators have developed Kt tables/nomographs for ducted and unducted propellers as a function of the ratio of propeller pitch to its Dp. Another way to determine Uo is to use the applied engine power – and as can be understood, the applied power during berthing and unberthing is usually less than the capacity – varying from some 10% to 35% of the installed capacity. . . . 2.2 Jet Exit Velocity Expansion and Implications Once Uo is generated, the next important question is what happens to it away from the ship. The afterward behavior of Uo is important because loading on structural elements and seabed depends on it. In the zone of afterward established flow the efflux must mix and dissipate by expanding and entraining the ambient water into the jet boundary. Observations have indicated that in this zone, efflux expands like a cone at an angle of about 12 degrees around the core of maximum velocity. The velocity across the cone decreases from the center following the Gaussian distribution. Along the distance behind the propeller – the whole cone velocity decreases exponentially away from the propeller. At a certain distance behind the propeller, the expanding jet comes in contact with the seabed, causing scour when the sediment pick-up threshold is exceeded. To illustrate the effects of an expanding jet on the seabed, I have included an image as an example – applicable for Dp = 2 m, n = 500 rpm, and Kt = 0.37. The estimated jet exit velocity Uo in this case is 16.2 m/s. The distance behind the propeller x and the height of the propeller axis above the flat seabed Zp are both normalized against Dp. The image shows how the jet velocity at the seabed increases and shifts toward the propeller as Zp decreases. At Zp/Dp = 1.0, the maximum is about 3.4 m/s. The change in Zp could occur, for instance due to the tidal rise and fall of water level, or to a small extent due to loading and unloading of a ship. In the example case, the maximum seabed velocities occurred at a distance x, from 5.3 to 6 times the Zp. The illustrated velocity is a time-averaged quantity – which means that instantaneous turbulence will likely register higher magnitude. Apart from turbulence, the second important one to cause higher velocity – is the effect of rudder behind a single propeller. The rudder splits the jet – and deflects it in one way or another depending on the ship’s heading requirement. At zero rudder deflection, the jet is split into two – one towards the water surface, the other towards the seabed – each making an angle of 12 degrees to the horizontal center – and each spreading at 10 degrees around the core. The implication of rudder deflection (maximum ~ 35 degrees) is that the jet-induced loading and scour phenomena could occur anywhere. The third is the twin-propeller setting with the rudder in the middle. The jets emanating from the two propellers are merged together at some distance (~ 10*Dp) behind the propeller. Unlike the rudder-behind single propeller setting, the deflecting power of the rudder is different, and the seabed velocity enhancement is expected to be less than the rudder-behind-a-single-propeller. However the propellers are often operated independent of each other, making predictions difficult. . . . 2.3 Other Aspects of the Propulsion System Some other aspects of ship propulsion systems are also important. There are the thrusters – bow and stern – usually having smaller propellers than the main ones – because of this fact they generate less jet exit velocity. Bow thrusters have mostly a transverse setting – meaning that they draw waters from one side to discharge them to the other – to help sidewise maneuvering of the bow. They mostly have high Zp – thus their effects on seabed are not critical – however the horizontal jets could impinge on quay walls or piles to cause substantial loading. Stern thrusters are mostly omni-directional and are located close to the keel, so that their Zp is rather low. They can play a critical role on causing significant seabed loading and scour. Ship design and propulsion systems are continually evolving (such as podded propulsors, azimuth thrusters and water jets) requiring refinement of known relations, and finding new ones. The consequences of high speed water jet propulsion systems on structures and seabed, open a different dimension to the propwash and associated loading impacts. Apart from these ship-related factors, there are other factors related to the berthing structure – pile orientation, proximity of the sloped bank behind the piles, vertical face sheet-pile walls, etc. All these factors are likely to complicate the jet loading – making the search for critical design conditions difficult – but one thing is certain, it is the potential conditions of repeated loading and incremental progression of damages – that dominate all design and operational considerations. . . . 3. Seabed Scour Protection and Propwash Loading on Structures Protecting the seabed against scour-related undermining of the structure foundation for low underkeel clearance setting can be very expensive. For the illustrated case with the maximum seabed velocity of 3.4 m/s, the theoretical median rock diameter is about 0.9 m. Accounting for turbulence factor and other uncertainties associated with rudder, and structural proximity, etc. the required design median rock diameter is likely to be even higher. For such cases, scour protection by bare rock riprap layers can appear impractical. There is an additional danger – it is the sucking-in velocity caused by a propeller with low underkeel clearance, which could suck-in smaller size rocks into the propeller – damaging it. Alternatives such as insitu concrete (such as concrete mattress, grouted rock) and prefabricated mattress (such as concrete block mattress, asphalt mattress, gabion mattress) provide promising options. Let me now briefly focus on another consequence of high jet exit velocity – and it is the drag force the velocity causes on piles supporting a berthing superstructure. To illustrate it simply, suppose there is an offshore marine terminal – a jacket structure standing on 20 m water. Together with dolphins, its purpose is to facilitate berthing, mooring and loading-unloading of oils or gas. A 10-m draft tanker berthing on this facility, likely un-assisted by Tugs, will berth and unberth at the same location repeatedly. If it is located in the Gulf of Mexico, with very little tidal range, it is highly likely that the tanker propeller jets will cause repeated drag loading at the same heights of the jacket-piles. For a case similar like this, the critical aspect is the localized repeated drag forces causing abrasion and bending of the piles. In this situation, the underkeel clearance is likely to be high; therefore any jet-induced seabed loading and scouring effect on the seabed may turn out to be negligible. . . . I like to stop at this – by finishing it with a tribute to Stephen Hawking (1942 – 2018) – who despite having debilitating illness did not stop from being active and pursuing his dream for finding a Unified Theory of Everything. He began the 1st paragraph of his book, A Brief History of Time with a little piece of humor: A well-known scientist (some say it was Bertrand Russell, 1872 – 1970) once gave a public lecture on astronomy. He described how the earth orbits around the sun and how the sun, in turn, orbits the centre of a vast collection of stars called our galaxy. At the end of the lecture, a little old lady at the back of the room got up and said: ‘What you have told us is rubbish. The world is really a flat plate supported on the back of a giant tortoise.’ The scientist gave a superior smile before replying, ‘What is the tortoise standing on?’ ‘You’re very clever, young man, very clever,’ said the old lady. ‘But it’s turtles all the way down!’ . . . . . - by Dr. Dilip K. Barua, 9 May 2018 |
Dr. Dilip K Barua
Archives
October 2024
Categories |
RSS Feed
