The World of Numbers and Chances

One must have guessed what I intend to discuss in this piece. People are glued to numbers in one way or another – for the sake of brevity let us say, from the data on finance, social demography and income distribution – to the scientific water level, wave height and wind speed. People say there is strength in numbers. This statement is mostly made to indicate the power of majority. But another way to examine the effectiveness of this statement is like this: suppose Sam is defending himself by arguing very strongly in favor of something. If an observer makes a comment like this, well these are all good, but the numbers say otherwise. This single comment has the power to collapse the entire arguments carefully built by Sam (unless Sam is well-prepared and able to provide counter-punch), despite the fact that numerical generalizations are invariably associated with uncertainties. Uncertainty is simply the lack of surety or absolute confidence in something.    
.  .  .
1. Numbers on an Uncertainty Paradigm
While the numbers have such powers, one may want to know:

1. What was the purpose and how were these numbers collected?
2. What is the attribution map to these numbers?
3. Are there identifiable patterns in these numbers?
4. If patterns exist, are they definite?
   
5. Are the different sets of numbers correlated or do they belong to some groups?
6. What is the likelihood of favorable outcomes of certain bins of numbers?
7. What is the likelihood of favorable outcomes of certain extreme numbers that may not have been sampled yet?
8. How certain are these likelihoods?
   
9. Is the knowledge conveyed by numbers adequate for decision making?
   

The science that answers all these questions on an uncertainty paradigm is known as statistics. This science is about the stochastic (as opposed to deterministic) world – the world driven by the messages conveyed by random (showing no easily identifiable systematic pattern) numbers, and the chances of favorable outcomes of those numbers. The former refers to, or is generally known as Statistics – the science of collection, organization, presentation and interpretation of numbers or numerical information. The latter as a sub-division of statistics, stands for Probability – the method of evaluating the likelihood of favorable outcomes of an event or hypothesis if sampled many times.
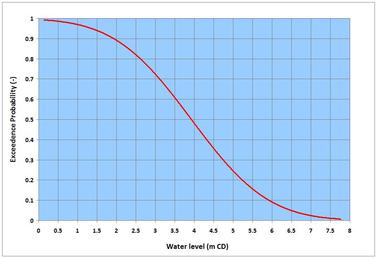
Probability with its root in logic is commonly known as probability distribution because it shows the distribution of a statistical data set – a listing of all the favorable outcomes, and how frequent they might occur (as a clarification of two commonly confused terms: probability refers to what is likely to happen – it denotes the surety of a happening but unsurety in the scale of its likelihood; while possibility refers to what might happen but is not certain to – it denotes the unsurety of a happening). Both of these methods aim at turning the information conveyed by numbers or data into knowledge – based on which inferences and decisions can be made. Statisticians rely on tools and methods to figure out the patterns and messages conveyed by numbers that may appear chaotic in ordinary views.
The term many times originates from the Theory of Large Numbers. Statisticians say that if a coin is tossed for a short period, for instance 10 times – it may yield let us say, 7 heads (70% outcome) and 3 tails (30% outcome); but if tossed many more times, the outcomes of the two possibilities, head and tail is likely to be 50% each – the outcomes one logically expects to see. Following the proof of this observation by Swiss mathematician Jacob Bernoulli (1655 – 1705), the name of the theory was formally coined in 1837 by French mathematician Simeon Denis Poisson (1781 – 1840).
There is a third aspect of statistics – it is known as the Statistical Mechanics (different from ordinary mechanics that deals with one single state) that is mostly used by physicists. Among others, the system deals with equilibrium and non-equilibrium processes, and Ergodicity (the hypothesis that the average over long time of a single state is same as the average of a statistical ensemble – an ensemble is the collection of various independent states).
.  .  .
2. Random and Systematic Processes
A few lines on the random and systematic processes. They can be discussed from the view points of both philosophical and technical angles. Randomness or lack of it, is all about perception – irrespective of what the numbers say, one may perceive certain numbers as random while others may see them differently. In technical terms, let me try to explain through a simple example. By building upon the Turbulence piece on the NATURE page, one can say that flow turbulent randomness appears when measurements tend to approximate to near-instantaneous sampling. Let us say, if one goes to the same spot again to measure turbulence under similar conditions; it is likely that the measurements would show different numbers. If the measurements are repeated again and again, a systematic pattern would likely emerge that could be traced to different causes – but the randomness and associated uncertainties of individual measurements would not disappear.
Something more on the randomness. The famous Uncertainty Principle proposed by German theoretical physicist Werner Karl Heisenberg (1901 – 1976) in 1926 changed the way science looks at Nature. It broke the powerful deterministic paradigm of Newtonian (Isaac Newton, 1642 – 1727) physics. The principle says that there can be no certainty in the predictability of a real-world phenomenon. Apart from laying the foundation of Quantum Mechanics, this principle challenges all to have a close look at everything they study, model and predict.                        
Among others, writing this piece is inspired after reading the books: A Brief History of Time (Bantam Books 1995) by British theoretical physicist Stephen Hawking (1942 - 2018); Struck by Lightning – the Curious World of Probabilities by JS Rosenthal (Harper Collins 2005); the 2016 National Academies Press volume: Attribution of Extreme Weather Events in the Context of Climate Change; and the Probability Theory – the Logic of Science by ET Jaynes (Cambridge University Press 2003). A different but relevant aspect of this topic – Uncertainty and Risk was posted earlier on this page indicating how decision making processes depend on shouldering the risks associated with statistical uncertainties.
On some earlier pieces on the NATURE and SCIENCE & TECHNOLOGY pages, I have described two basic types of models – the behavioral and the process-based mathematical models – the deterministic tools that help one to analyze and predict diverse fluid dynamics processes. Statistical processes yield the third type of models – the stochastic or probabilistic models – these tools basically invite one to see what the numbers say to understand the processes and predict things on an uncertainty paradigm. While the first two types of models are based on central-fitting to obtain mean relations for certain parameters, the third type looks beyond the central-fitting to indicate the probability of other occurrences.  
.  .  .
3. Frequentist and Bayesian Statistics
Before moving further, a distinction has to be made. What we have discussed so far is commonly known as the classical or Frequentist Statistics (given that all outcomes are equally likely, it is the number of favorable outcomes of an event divided by the total outcomes). Another approach known as the Bayesian Statistics was proposed by Thomas Bayes (1701 – 1761) – developed further and refined by French mathematician Pierre-Simon Laplace (1749 – 1827). Essentially, this approach is based on the general probability principles of association and conditionality.
Bayesian statisticians assume and use a known or expected probability distribution to overcome, for instance, the difficulties associated with the problems of small sampling durations. It is like infusing an intuition (prior information or knowledge) into the science of presently sampled numbers. [If one thinks about it, the system is nothing new – we do it all the time in non-statistical opinions and judgments.] While the system can be advantageous and allows great flexibility, it also has room for manipulation in influencing or factoring frequentist statistical information (that comes with confidence qualifiers) in one way or another.
.  .  .
4. History of Statistics
Perhaps a little bit of history is desirable. Dating back from ancient times, the concept of statistics existed in all different cultures as a means of administering subjects and armed forces, and for tax collection. The term however appeared in the 18th century Europe as a systematic collection of demographic and economic data for better management of state affairs. It took more than a century for scientists to formally accept the method. The reason for such a long gap is that scientists were somewhat skeptical about the reliability of scattered information conveyed by random numbers. They were more keen on robust and deterministic aspects of repeatability and replicability of experiments and methods that are integral to empirical science.
Additionally, scientists were not used to trust numbers that did not accompany the fundamental processes causing them. Therefore, it is often argued that statistics is not an exact science. Without going into the details on such arguments, it can be safely said that many branches of science including physics and mathematics (built upon theories, and systematic uncertainties associated with assumptions and approximations) also do not pass the exactitude (if one still believes this term) of science. 
In any case as scientists joined, statistical methods received a big boost in sophistication, application and expansion (from simple descriptive statistics to many more advanced aspects that are continually being refined and expanded). Today statistics represents a major discipline in Natural and social sciences; and many decision processes and inferences are unthinkable without the messages conveyed or the knowledge generated by the science of numbers and chances. However, statistically generalized numbers do not necessarily tell the whole story, for instance when it comes down to human and social management – because human mind and personality cannot simply be treated by a rigid number. Moreover, unlike the methods scientists and engineers apply, for instance, to assess the consequences and risks of Natural Hazards on vulnerable infrastructure – statistics-based social decisions and policies are often biased toward favoring the mean quantities or majorities at the cost of sacrificing the interests of vulnerable sections of the social fabric.                       
When one reads the report generated by statisticians at the 2013 Statistical Sciences Workshop (Statistics and Science – a Report of London Workshop on the Future of Statistical Sciences) participated by several international statistical societies, one realizes the enormity of this discipline encompassing all branches of Natural and social sciences. Engineering and applied science are greatly enriched by this science of numbers and chances.                    
.  .  .
5. Probability and Statistical Distributions
In many applied science and engineering practices, a different problem occurs – that is how to attribute and estimate the function parameters for fitting a distribution in order to extrapolate the observed frequency (tail ends of the long-term sample frequencies, to be more specific) to predict the probability of an extreme event (which may not have occurred yet). The applied techniques for such fittings to a distribution (ends up being different shapes of exponential asymptotes) of measurements are known as the extremal probability distribution methods.
They generally fall into a group known as the Generalized Extreme Value (GEV) distribution – and depending on the values of location, scale and shape parameters, they are referred to as Type I (or Gumbel distribution, German mathematician Emil Julius Gumbel, 1891 – 1966), Type II (or Fisher-Tippett distribution, British statisticians Ronald Aylmer Fisher, 1890 – 1962 and Leonard Henry Caleb Tippett, 1902 – 1985) and Type III (or Weibull distribution, Swedish engineer Ernst Hjalmar Waloddi Weibull, 1887 – 1979).
This in itself is a lengthy topic – hope to come back to it at some other time. For now, I have included an image I worked on, showing the probability of exceedence of water levels measured at Prince Rupert in British Columbia. From this image, one can read for example, that a water level of 3.5 m CD (Chart Datum refers to bathymetric vertical datum) will be exceeded for 60% of time (or that water levels will be higher than this value for 60% of time, and lower for 40%). In extreme probability distribution it is common practice to refer to an event in recurrence intervals or return periods. This interval in years says that an event of a certain return period has the annual probability – reciprocal of that period (given that the sampling refers to annual maxima or minima). For example, in a given year, a 100-year event has 1-in-100 chance (or 1%) of occurring.
Another distinction in statistical variables is very important – this is the difference between continuous and discrete random variables. Let me try to briefly clarify it by citing some examples. The continuous random variable is like water level – this parameter changes and has many probabilities or chances of occurring from 0 (exceptionally unlikely) to 1 (virtually certain). In many cases, this type of variables can be described by Gaussian (German mathematician Carl Freidrich Gauss, 1777 – 1855) or Normal Distribution. The discrete random variable is like episodic earthquake or tsunami events – which are sparse and do not follow the rules of continuity, and can best be described by Poisson Distribution.           
.  .  .
6. Making Sense of Numbers
When one assembles huge amounts data, there are some first few steps one can do to understand them. Many of these are described in one way or another in different text books – I am tempted to provide a brief highlight here.

1. A first impression on the quality of data can always be made by deciphering the documentations on the collection platforms, instrumentation, methodology, etc.
   
2. Next, it is always helpful to make a plot of the data in order to make a preliminary assessment of scatter or cluster, errors, outliers, shift (could result from datum change, change in the instrumentation configuration, etc.) periodicity, and trend if any. These first two steps are very important for screening and validating the collected information.
3. The next important step is to do some descriptive statistics – the central tendency (the location parameter – mean, median, and mode), their spread around the center (the scale parameter – the standard deviation, STD) and the shape parameter (symmetry/asymmetry, peak). The simplest and the most prevalent distribution yielding these parameters is the symmetric Normal Distribution – typical of continuous random variables. In this distribution, the larger the standard deviation the larger is the data scatter – with 68%, 95% and 99.8% of data lying within ±1 STD, ±2 STD and ±3 STD of the mean, respectively. In coastal waters, sea-state waves follow a skewed or asymmetric distribution – the Rayleigh Distribution (Lord Rayleigh, 1842 -1919). Whatever distribution is applicable, the data are usually presented in PDF (probability density function), CPD (cumulative probability distribution) or EPD (exceedence probability distribution). The first represents the occurrence probability; the last two are comparative probabilities.    
   
4. Most continuous random variables represent a superimposed multiplicity of information belonging to different frequencies, amplitudes and phases. Application of the Fourier Transform (Jean-Baptiste Joseph Fourier, 1768 – 1830) routines is helpful to decompose the data into different components. This is useful for finding out the dominating frequencies, the periodicity or trend in the data.
5. Depending on the purpose, one can then choose to remove some frequencies from the data by applying an appropriate filter. One such is the Low-Pass Filter (LPF) that passes information of frequencies lower than a cut-off frequency, and attenuates the higher frequencies. The other is the High-Pass Filter (HPF) – passing frequencies higher than a cut-off frequency and attenuating the lower frequencies. Moving average techniques are also applied for similar purposes.
   
6. Looking into the stationarity of data is very important. Stationarity simply means that no upward or downward trend is evident in the data when moving averages are applied. Stationarity or non-stationarity has serious implications in future projections (such as GEV distributions – which are based on the assumption that data are stationary), for example of climate change and consequences.  Let me cite one simple example. The water level that one measures at a tidal station has many components – the highest period being the Nodal Period of 18.6 years – this period is caused by the oscillating inclination of the Moon’s orbit relative to the plane of the Earth’s Equator. This factor induces a subtle and small change in the time-series water level data – therefore Mean Sea Level is determined by averaging over this period. It is understandable that any prediction of climate change induced Sea Level Rise trend must take account of such factors to eliminate the undesirable frequencies.      
   
7. There are some other analyses – statisticians use to make sense of large amount of multi-variate data, applied especially in climate, social and biological sciences. One of them is known as Cluster Analysis – referring to grouping or clustering, such that data in each group have more similar attributes or characteristics than the ungrouped data. The Principal Component Analysis (PCA) – is one such technique – it is a tool for identifying the patterns in data, and expressing the data in a way to highlight their similarities and differences. Among others, COVARIANCE evaluations are made to determine the strength of data correlation (if COV is 0, +ve or -ve, the variables are uncorrelated, positively correlated, and negatively correlated, respectively). 
   

7. Conditional Probability
Before finishing I like to illustrate a case of conditional probability, applied to specify the joint distribution of wave height and period. These two wave properties are statistically inclusive and dependent; and coastal scientists and engineers usually present them in joint frequency tables. As an example, the joint frequency of the wave data collected by the Halibut Bank Buoy in British Columbia shows that 0.25-0.5 m; 7-8 s waves occur for 0.15% of the time. As for conditional occurrence of these two parameters, analysis would show that the probability of 7-8 s waves is likely 0.52% given the occurrence of 0.25-0.5 m waves; and that of 0.25-0.5 m waves is likely 15.2% given the occurrence of 7-8 s waves.
This piece ended up into a long one than I anticipated.
.  .  .
Here is a piece of caution stated by a 19th century British statesman, Benjamin Disraeli (1804 – 1881): There are three kinds of lies: lies, damned lies, and statistics. Apart from bootstrapping, lies are ploys designed to take advantages by deliberately manipulating and distorting facts. The statistics of Natural sciences are less likely to qualify for lies – although they may be marred with uncertainties resulting from human error, data collection techniques and methods (for example, the data collected in the historic past were crude and sparse, therefore more uncertain than those collected in modern times).
​Data of various disciplines of social sciences, on the other hand are highly fluid in terms of sampling focus, size, duration and methods, in data-weighing, or in the processes of statistical analyses and inferences. Perhaps that is the reason why the statistical assessments of the same socio-political-economic phenomena by two different countries hardly agree, despite the fact that national statistical bodies are supposedly independent of any influence or bias. Perhaps such an impression of statistics was one more compelling reason for statistical societies to lay down professional ethics guidelines (e.g. International Statistics Institute; American Statistical Society).

.  .  .  .  .

- by Dr. Dilip K. Barua, 19 January 2018

---