Wave Forces on Slender Structures

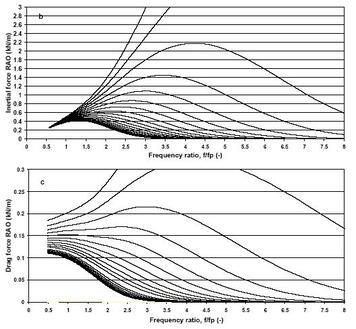Most of the materials in this piece are based on my 2008 ISOPE (International Society of Offshore and Polar Engineers) paper: Wave Loads on Piles – Spectral Versus Monochromatic Approach. This paper discusses, for both monochromatic and spectral waves, how the Morison forces (Morison and others, 1950) compare for a surface piercing round vertical pile in some cases of waves with Ursell Numbers (Fritz Joseph Ursell, 1923 – 2012), U in the order of 5.0. I have included an image (courtesy ISOPE) from this paper showing inertial and drag force RAOs as a function of frequency. The RAO or Response Amplitude Operator represents the maximum force for a unit wave height.
.  .  .
Standing in the nearshore water of unbroken waves, one experiences a shoreward push when a wave crest passes and a seaward pull when a wave trough passes – and if the waves happen to be large he or she may experience dislodging from the foothold. The immediate instinct is to recognize the power of a wave in exerting forces on members standing on its way – resisting its motion. How to estimate these forces? Do structures of all different sizes experience the same type of forces?
The answer to the first question depends on how well one answers the second question – how the structure sizes up with the wave – the wave length (L) to be exact. It turns out that the nature of wave forces on a structure can be distinguished based on the value of a parameter known as the diffraction parameter – a ratio of the structure dimension (D) perpendicular to the direction of wave advance, and the local wave length, L. When D is less than about 1/5th of L, the structure can be treated as slender and wave forces can be determined by the Morison equation.
.  .  .
In this piece let us attempt to see how the Morison forces work – how the forces apply in considerations of both monochromatic and spectral waves. I will also touch upon the nonlinear wave forces. Slender structures exist in many port and offshore installations as vertical structures – as mono pile and pile-supported wharfs in ports – as gravity platforms and jacket structures in offshore structures – and as horizontal structural members and pipelines.
What are the Morison forces? They are the forces caused by the wave water particle kinematics – the velocity and acceleration. The two kinematics causing in-line drag and inertial horizontal forces are hyperbolically distributed over the height of a vertical standing structure – decreasing from the surface to the bottom. For a horizontal pipeline, the loads include both the in-line horizontal forces as well as the hydrodynamic vertical lift force. More about these to-and-fro wave forces? The drag force is due to the difference in the velocity heads between the stoss and lee sides of the structure; and the inertial force is due to its resistance to water particle acceleration.
The hydrodynamic lift force is due to the difference in flow velocities between the top and bottom of a horizontal structure. I will attempt to talk more about it at some other time. Do the slender members change the forcing wave character? Well while the structures provide the resistances by taking the forces upon themselves; they are not able to change the character of the wave – because they are too small to do so. 
From the perspectives of structural configuration, when a vertical member is anchored to the ground but free at the top, it behaves like a cantilever beam subjected to the hyperbolically distributed oscillating horizontal load. When rigid at both ends, the member acts like a fixed beam. For a horizontal pipeline supported by ballasts or other rigidities at certain intervals, it also acts like a fixed beam with the equally distributed horizontal drag and inertial forces and the vertical hydrodynamic lift forces.    
.  .  .
Before entering into the complications of spectral and nonlinear waves, let us first attempt to clarify our understanding of how linear wave forces work. We have seen in the Linear Waves piece on the NATURE page that the wave water particle orbital velocity is proportional to the wave height H, but inversely proportional to the wave period T. The water particle acceleration is similarly proportional to H, but inversely proportional to T^2. The nature of proportionality immediately tells us that waves of low steepness (H/L) have lower orbital velocities and accelerations – therefore they are able to cause less forces than the waves of high steepness. For symmetric or linear waves, the orbital velocity and acceleration are out of phase by 90 degrees.
In the light of Bernoulli Theorem (Daniel Bernoulli, 1700 – 1782) dealing with the dynamic pressure and velocity head, the drag force is proportional to the velocity squared. Both the drag and inertial forces must be multiplied by some coefficients to account for the structural shape and for viscosity of water motion at and around the object. Many investigators devoted their times to find the appropriate values of drag and inertia coefficients. A book authored by T. Sarpkaya and M. Isaacson published in 1981 has summarized many different aspects of these coefficients.
Among others the coefficients depend on the value of Reynolds Number (Osborne Reynolds, 1842 – 1912) – a ratio of the product of orbital velocity and structure dimension to the kinematic viscosity. The dependence of the forces on the Reynolds Number suggests that a thin viscous sublayer develops around the structure – and for this reason the Morison forces are also termed as viscous forces. The higher the value of the Reynolds Number, the lower are the values of the coefficients. The highest drag and inertial coefficients are in the range of 1.2 and 2.5, respectively, but drag coefficients as high as 2.0 have been suggested for tsunami forces.
.  .  .
How do the drag and inertial forces compare to each other? Two different dimensionless parameters answer the question. The first is known as Keulegan-Carpenter (G.H. Keulegan and L.H. Carpenter, 1958) Number KC; it is directly proportional to the product of wave orbital velocity and period and inversely proportional to the structure dimension. It turns out that when KC > 25 – drag force dominates, and when KC < 5 inertia force dominates. The other factor is known as the Iversen Modulus (H.W. Iversen and R. Balent, 1951) IM, is a ratio of the maximums of inertia and drag forces. It can be shown that both of these two parameters are related to each other in terms of the force coefficients.    
While the horizontal Morison force is meant to result from the phase addition of the drag and inertial forces, which are 90 degrees out of phase, the conventional engineering practice ignores this scientific fact, instead adds the maximums of the two together. This practice adds a hidden factor of safety (HFS) in design forces. For example, a 2-meter, 12-second wave acting on a 1-meter vertical structure standing at 20-meter of depth (U = 6.4) would afford a HFS of 1.45. However HFS varies considerably with the changing values of IM – with the highest occurring at IM = 1.0, but decreases to unity at very high and low values of IM. 
How does the wave nonlinearity affect the Morison forces? We have seen in the Nonlinear Waves piece on the NATURE page that the phase difference between the velocity and acceleration shifts away from 90 degree – with the increasing crest water particle velocity and acceleration. For the sake of simplicity, let us focus on a 1-meter high 8-second wave, propagating from the region of symmetry at 10 meter water depth (U = 5.0) to the region of asymmetry at 5 meter water depth (U = 22.6). By defining and developing a relationship between velocity and acceleration with U, it can be shown the maximum linear and nonlinear forces are nearly equal to each other at U = 5.0. But as the wave enters into the region of U = 22.6, the nonlinear drag force becomes 36% higher than the linear drag force. The nonlinear inertia force becomes 8% higher than the linear one. With waves becoming more nonlinear in shallower water, the percentage increases manifold higher than the ones estimated by the linear method.
While the discussed method provides some insights on the behaviors of nonlinear Morison forces, USACE (US Army Corps of Engineers) CEM (Coastal Engineering Manual) and SPM (Shore Protection Manual) have developed graphical methods to help estimating the nonlinear forces.  
.  .  .  
Now let us turn our attention to the most difficult part of the problem. What happens to the Morison forces in spectral waves? How do they compare with the monochromatic forces? To answer the questions, I will depend on my ISOPE paper. The presented images from this paper shows the inertial and drag force RAOs over the 20-meter water depth at 1-meter interval from the surface to the bottom – for a 2-meter high 12-second wave acting on a 1-meter diameter round surface-piercing vertical pile. The forcing spectral wave is characterized by JONSWAP (Joint North Sea Wave Project) spectrum (see Wave Hindcasting).
For this case, the RAOs are the highest at frequencies about 3.5 times higher than the peak frequency (fp) of 0.08 Hertz (or 12-second). This is interesting because the finding is contrary to the general intuition that wave forces are high at the frequency of the peak energy – the period effects on wave kinematics! As the frequency decreases, the inertial force RAO diminishes tending to zero. The drag force RAO, on the other hand, tends to reach a constant magnitude as the frequency decreases. This finding confirms that at low frequency motions of tide and tsunami, the dominating force is the drag force (which is also true for cases when KC > 25.0).
How do the spectral wave forces compare with the monochromatic wave forces? It turns out that for the case considered, the monochromatic method underestimates the wave forces by about 9%. A low difference of this order of magnitude is good news because one can avoid the rigors of the spectral method to overcome such a small difference – the difference of this magnitude is in the range of typical uncertainties of many parameters. 

.  .  .  .  .

- by Dr. Dilip K. Barua, 17 November 2016                              

---