Wave Structure Interactions & Scour

I like to begin this piece with a line from Socrates (469 – 399 BCE) who said: I am the wisest man alive, for I know one thing, and that is that I know nothing. This is a philosophical statement developed out of deep realization – neither practical nor useful in the mundane hustle-bustle of daily lives and economic processes. Philosophers tend to see the world differently sometimes beyond ordinary comprehension – but something a society looks upon to move forward in the right direction. Scientists and engineers – for that matter any investigator, who explores deep into something, comes across this type of feeling nonetheless – the feeling that there appear more questions than definitive answers. This implies that our scientific knowledge is only perfect to the extent of a workable explanation or solution supported by assumptions and approximations – but in reality suffers from transience embedded with uncertainties. This piece is nothing about it – but an interesting aspect of actions and reactions between waves and structures.    
.  .  .
1. Conservation of Wave Energy
One of the keys to understanding these processes – for that matter any dynamic equilibrium of fluid flow – is to envision the principle of the conservation of energy – that the incident wave energy must be balanced by the structural responses – the processes of dissipation, reflection and transmission. These interaction processes cause vortices around the structure scouring the seabed and undermining its stability. Let me share all these aspects in a nutshell. As done in other pieces – I will provide some numbers to give an idea what we are talking about.
The materials covered in this piece are based on my experience in different projects; and on the materials described in: the Random Seas and Design of Maritime Structures (Y. Goda 2000); the 2002 Technical Report on Wave Run-up and Wave Overtopping at Dikes (The Netherlands); the 2006 USACE Coastal Engineering Manual (EM 1110-2-1100 Part VI); the 2007 Eurotop Wave Overtopping of Sea Defences and Related Structures (EUROCODE Institutes); the 2007 Rock Manual of EUROCODE, CIRIA (Construction Industry Research and Information Association) and CUR (Civil Engineering Research and Codes, the Netherlands); and others.
Most of the findings and formulations in wave-structure interactions and scour are empirical – which in this context means that they were derived from experimental and physical scale modeling tests and observations in controlled laboratory conditions – relying on a technique known as the dimensional analysis of variables. Although they capture the first order processes correctly, in real world problems the formulation coefficients may require judgmental interpretations of some sort to reflect the actual field conditions. 
Some materials relevant for this piece were covered earlier in the NATURE and SCIENCE & TECHNOLOGY pages. This topic can be very elaborate – and to manage it to a reasonable length, I will limit it to discussing some selected aspects of:

• reflection (a portion of the waves reflecting back into the incident waves by the structure);
  
• runup (the vertical height of the wave up-rush along a sloping structure or beach after breaking);
  
• transmission over a fixed breakwater (a portion of the waves propagating across a submerged structure, or the overtaken runup spilling over the structure crest into the back area), or through a floating breakwater (a portion of the waves passing through underneath a floating structure);
  
• overtopping (the runup reaching and overtaking the crest of the structure);
  
• and scour (the obstruction created by the structure creating nearfield vortices to scour erodible seabed within the immediate vicinity of the structure).
  

Among these: runup, overtopping and scour represent processes that consume or dissipate a portion of the incident wave energy. The two other relevant phenomena – diffraction (bending of the incident waves around a structure) and scattering (waves reflecting from the structure in multiple directions fragmenting the incident wave) are not covered in this piece. Hope to come back to them at some other time.
.  .  .
2. Wave Structure Interactions
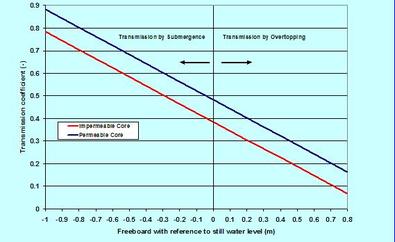
What must one look for to describe the wave-structure interactions? Perhaps the first is to realize that only the waves with lengths (L) less than about 5 times the structures dimension (D) are poised to cause wave-structure interactions (see the Wave Forces on Slender Structures on this page) in the presence of slender structures. The second is that the wave energy must remain in balance – which translates to the fact that sum of squares of the wave heights (H^2) in dissipation, reflection and transmission must add to the incident wave height squared. This balancing is usually presented in terms of coefficients (the ratios of dissipated, reflected and transmitted wave heights to the incident wave height), squares of which (C^2) must add to one. The third is the Surf Similarity Number (SSN, discussed in The Surf Zone on this page) – this parameter appears in every relation where a sloping structure is involved – it is directly proportional to wave period and slope. The fourth is the direction of wave forcing relative to the loading face of the structure – its importance can simply be understood from the differences in interactions between the head-on and oblique waves. Importance of other structural parameters will surface as we move on to discussing the processes.    
.  .  .
2.1 Wave Reflection
Wave reflection can be a real problem for harbors lined with vertical-face seawalls. It can cause unwanted oscillation and disturbance in vessel maneuvering and motion, and in the scouring of protective structure foundations. As one can expect, wave reflection from a vertical-face smooth structure is higher than and different from a non-overtopped sloping structure. A non-breaking head-on wave on a smooth vertical-face structure is likely to reflect back straight into the incident waves – an example of perfect reflection. When waves are incident at an angle on such a structure, the direction of the reflected waves follows the principle of optical geometry.           
For sloping structures, the reflection is directly proportional to SSN, and it can be better grasped from a relation proposed by Postma (1989). Let us see it through an example. A 1-m high wave with periods of 6-s and 15-s, propagating head-on, on a non-overtopped 2 to 1 straight sloping stone breakwater (with a smooth surface and an impermeable core) would produce reflected waves in the order of 0.36 m and 0.83 m, respectively. When the slope is very rough built by quarried rock, most of the incident energies are likely to be absorbed by the structure. It is relevant to point out that according to Goda (2000), natural sandy beaches reflect back some 0.25% to 4% of incident wave energies.                 
.  .  .
2.2 Wave Runup
Wave runup is an interesting phenomenon – we see it each time we are on the beach – not to speak of the huge runups that occur during a tsunami overwhelming us in awe and shock. The runup is a way for waves to dissipate its excess energy after breaking. Different relations proposed in literature show its dependence on wave height and period, the angle of wave incidence, beach or structure slope – and on the geometry, porosity and roughness. A careful rearrangement of different proposed equations would indicate that the runup as directly and linearly proportional to wave period and slope, but somewhat weakly to wave height. This is the reason why the runup of a swell is higher than a lower-period sea – or why a flatter slope is likely to have less runup than a steeper one – or why the tsunami runup is so huge. An estimate following the USACE-EM would show that the maximum runups on a 10 to 1 foreshore beach slope are 1.9 m and 3.8 m for a 1-m high wave with periods of 6-s and 15-s, respectively. 
The explanation of the runup behavior is that the longer the wave period, the less is its loss of energy during breaking, affording the runup process to carry more residual energy. Although a runup depends on its parent oscillatory waves for energy, its hydrodynamics is translatory, dominated by the laws of free surface flows – this means in simple terms – the physics of the steady Bernoulli (Daniel Bernoulli; 1700 – 1782) equation.
.  .  .
2.3 Wave Transmission
How does the wave transmissions over and through a maritime structural obstacle work? Such structural obstacles are called breakwaters because they block or attenuate wave effects in order to protect the areas behind them. There are two basic types – the fixed or rigid, and the floating breakwaters. The former is usually built as a thin-walled sheet pile, a caisson or as a sloped rubble-mound (built by quarried rocks or other manufactured shapes). The second, moored to seabed or fixed to vertical mono-piles, is usually built by floats with or without keels. The floating breakwaters are only effective in a coastal environment of relatively calm short period waves (the threshold maximum ≈ 4 s) – because long period waves tend to transmit easily with negligible loss of energy. The attenuation capacity of such breakwaters is often enhanced by a catamaran type system by joining two floats together.    
First let us have a glimpse of wave transmissions over a submerged and overtopped fixed breakwater. To illustrate this over a low-crested (structure crest height near the still water level – somewhat higher and lower) rubble-mound breakwater, an image is included showing the transmission coefficients (ratio of transmitted to incident wave height) for a head-on 1-m high 6-s wave, incident on the 2 to 1 slope of a breakwater with a crest width of 1 m. This is based on a relation proposed by researches at Delft (d’Angremond and others 1996) and shows that with other factors remaining constant, the transmission coefficient is linearly but inversely proportional to the freeboard. For both the permeable and impermeable cores, the image shows the high transmission by submergence (often termed as green overtopping) and low transmission by overtopping – with the permeable core affording more transmissions than a non-permeable one. Emergent and submergent with the changing tide level, such transmissions are directly proportional to wave height, period and stoss-side breakwater slope, but inversely proportional to the breakwater crest width.                         
Wave transmission concept over a submerged breakwater is used to design artificial reefs to attenuate wave effects on an eroding beach. In another application, the reef layout and configuration are positioned and designed in such a way that wave focusing is stimulated. The focused waves are then led to shoal to a high steepness suitable for surfing – giving the name artificial surfing reef. 
The transmissions through a floating breakwater are complicated – more for loosely moored than a rigidly moored. As a rule of thumb, an effective floating breakwater requires a width more than half the wave length, or a draft at least half the water depth. To give an idea, an estimate would show that for a 1-m high, 4-s head-on incident wave on a single float with a width of 2 m and a draft of 2 m – rigidly moored at 5 m water-depth – the transmitted wave height immediately behind would be 0.55 m. If the draft is increased to 2.5 m by providing a keel, the transmitted wave heights would reduce to 0.45 m. The estimates are based on Weigel (1960), Muir Wood and Fleming (1981), Kriebel and Bollmann (1996) and Cox and others (1998).
.  .  .
2.4 Wave Overtopping
Wave overtopping is a serious problem for the waterfront seawalls installed for protecting urban and recreational areas from high storm waves. It disrupts normal activities and traffic flow, damages infrastructure and causes erosion. Among the various researches conducted on this topic, the Owen (1982) works at the HR Wallingford shows some insights into the overtopping discharge rates.
Overtopping discharge rate is directly proportional to the incident wave height and period, but inversely to the freeboard (the height of the structure crest above still water level). To give an idea: for a 1 m high freeboard, 2 to 1 sloped structure – a 1-m high wave with periods of 6-s and 15-s would have an overtopping discharge of 0.10 and 0.82 m^2/s per meter width of the crest, respectively. If the freeboard is lowered to 0.5 m, the same waves will cause overtopping of 0.26 and 1.25 m^2/s/m.   
.  .  .
2.5 Scour
Scouring of erodible seabed in the vicinity and around a structure results from the obstruction of a structure to fluid flows. The obstructed energy finds its way in downward vertical motions – in the nearfield vigorous actions and vortices scooping out sediments from the seabed. Scouring processes are fundamentally different from the erosion processes – the latter is a farfield phenomenon and occurs due to shearing actions. The closest analogies of the two processes are like this: the vortex scouring action is like a wind tornado – while the process of erosion is like the ground-parallel wind speed picking up and blowing sand. 
Most coastal scours occur in front of a vertical sea wall, near the toe of a sloping structure, at the head of a breakwater, around a pile, and underneath a seabed pipe. They are usually characterized by the maximum depth of scour (an important parameter indicating the undermining extent of scouring), and the maximum peripheral extent of scouring action. It turns out that these two scouring dimensions scale with wave height, wave period, water depth and structural diameter or width. These parameters are lumped into a dimensionless number known as the  Keulegan-Carpenter (KC) Number (a ratio of the product of wave period and nearbed wave orbital velocity to the structure dimension), proposed by GH Keulegan and LH Carpentar (1958). This number was introduced in the Wave Forces on Slender Structures piece on this page.
​Experimental investigations by Sumer and Fredsøe (1998) indicate that a scour hole around a vertical pile develops only when KC > 6. At this value, wave drag starts to influence the structure adding to the inertial force, and scouring action continues to increase exponentially as the KC and structure diameter increase. Scour prevention is mostly implemented by providing stone ripraps – of suitable size, gradation and filter layering.
.  .  .
The Koan of this piece:
If you do not respect others – how can you expect the same from them.

.  .  .  .  .

- by Dr. Dilip K. Barua, 20 October 2017     

---