 Wave asymmetry or nonlinearity was the primary focus of three pieces posted earlier – Nonlinear Waves, Spectral Waves and Upslope Events and Downslope Processes. The latter and the piece on Symmetry, Stability and Harmony discussed different implications of asymmetry both in the dynamics of Natural processes and in Social Interactions. The asymmetric processes begin right after a wave is born – in the energy transformations of action-reaction-duo of different frequencies, phases and amplitudes – caused by those that impart energy to those that interact and dissipate it. In the end, a visible Natural wave is a showcase of imbalance or asymmetry built by multiple waves – sometimes portraying an incomplete circle or closure – at other times leaving an overflowing residual in the direction of dominant motion. An easily understandable schematic relation of the processes – related to the water motion dynamics illustrated in the Navier-Stokes Equation – is presented in my 2017 Springer Encyclopedia chapter.
Perhaps incoherence or absence of synchronicity among the parameters of a system – often visible in wide scatter or outlier – has a tone similar to that of asymmetry. Both asymmetry and incoherence define Nature and its dynamic processes – because they are the reflections of ever changing fluxes of action-reaction-duo. They are an indication of disorder in quests for establishing order or equilibrium (see Entropy and Everything Else; Warming Climate and Entropy and Upslope Events and Downslope Processes). Therefore, while addressing and characterizing the wave asymmetry – this piece will also have indications of the existence of incoherence within the wave system parameters. It primarily addresses the long and short wave asymmetries – highlighting some gists of what are commonly known, and of some that are not. The former is based on my dissertation and a manuscript I worked on. The latter on a method I have developed – and will be discussed for the example wave presented in earlier pieces (see Linear Waves and Nonlinear Waves). The purpose of the latter part, is to demonstrate the usefulness of Ursell Number (Fritz Joseph Ursell, 1923 – 2012) to characterize the degree of wave symmetry/asymmetry in quantitative numbers. The number (U = HL^2/d^3) integrates three easily determinable wave parameters – the height (H) and local length (L) of a wave at still water depth (d). They are based on some of my unpublished works – devoted in initiatives to search for better and simple analytical tools. As pointed out in earlier pieces, investigators credited to develop the foundational basics of nonlinear wave theories (see Ocean Waves; Transformation of Waves; Linear Waves; Nonlinear Waves; Spectral Waves; and Waves – Height, Period and Length) include: Stokes (British mathematician George Gabriel Stokes (1819 – 1903); Skjelbriea et al (1960); RG Dean (1965); Dalrymple (1974); and Chaplin (1980). . . . 1. Wave Asymmetry Intro Before going into the topic, perhaps a few words on my advanced research on the phenomena of waves are useful. In my Ph. D. Dissertation (The University of South Carolina 1992) and in the 1990 and 1994 Elsevier publications, the measured and modeled nonlinearity of tidal wave and the associated consequences on sediment transport and sedimentation were discussed for the coastal ocean (see my 1991 ASCE Coastal and Ocean Management Symposium paper) off the Ganges-Brahmaputra-Meghna (GBM) river system mouth. The works were made possible – by the kind supports of NSF grants through Prof WS Moore and Prof SA Kuehl at the University of South Carolina. Other kind supports from committee members included: Prof B Kjerfve (coastal and estuarine hydrodynamics), Dr TW Kana (sediment and wave dynamics; the 1995 JCR publication). They are supplemented by unfailing additional kind supports of: WD Eysink and FG Koch of Delft Hydraulics (sediment transport and sedimentation), Prof A Nishat of BUET (Coastal Hydraulics and Bangladesh coast), and the Bangladesh Water Development Board. Capt Neinhuis, Romke van der Wal and Bart Peerbolte of Delft Hydraulics - the three unfailing friends who were the source of inspiration in the beginning of my career. An article posted later Coastal Ocean Currents off Rivermouths presents a synopsis of the 2nd Chapter of my Dissertation. A few words on a wave of unusual type – its scale covers the whole year of the annual hydrologic cycle. It is the seasonal river discharge, and is unusual because there is no reversal of flow – rather it has the wave-type: fall-rise-fall-rise water level stages. In the Bangladesh Reach of the Brahmaputra-Jamuna River, some 7 distinct stages can be identified from the flat low during the January-February dry period to the varying peaks in July-August wet season (my 1997 Water Nepal paper). As also discussed in the Environmental Controls and Functions of a River – observations in the Bangladesh Reach of the Ganges River (my 1995 IEB paper), indicated that the river flows can be characterized in terms of a Seasonality Index (this parameter defines the river regime and is very useful to distinguish the hydrologic characteristics of one river from another) – with a rather steeper slope during the rising phase than the falling period. The implication of such an asymmetry lies in the existence of the so-called hysteresis or incoherence in the relationship between river stage and discharge – and between the discharge and sediment transport. . . . 2. The Long Wave This part is on long wave (L/d ≥ 20; see Ocean Waves) asymmetry and system incoherence – tidal motion in particular. It is based on portion of my dissertation works (Chapter 2 of Dissertation – Tidal Currents and residual flow field in the Coastal Ocean of Bangladesh) – that is in line with Prof Kjerfve’s expertise; an unpublished manuscript, my 1991 PIANC-COPEDEC III paper, and on some of my later works (e.g. in Lynn Canal, Alaska; in Prony Bay, Kwé Bay and Havannah Canal, New Caledonia; and in Chapaco Bay, Chile). I will broaden the tidal wave asymmetry by covering the processes that lead to it and how it is presented to visualize the nature of asymmetry – or sometimes as coherence/incoherence. First, as most of us are very familiar with – the wave asymmetry can be immediately visualized when time-series tidal elevations measured at a station (often referred to as Eulerian) are plotted – showing the difference in the slopes of rising climb and falling descent, and the difference in the nature of crest (peakedness) and trough (flattening) shapes. The pattern, degree and trend of nonlinearity or asymmetry (such as in deformation, amplification and damping) can be recognized when time-series of multiple stations are plotted together. They are indicative of the wave transformation – that results from the effects of bathymetry/topography and unidirectional currents, if any. Second, a quantification of tidal wave asymmetry can best be done by harmonic decomposition of the wave (the decomposition yields symmetric harmonic waves of different amplitudes, frequencies and phases; see my COPEDEC III paper as an example). This method is very illuminating to identify and assess – how an incident or parent tidal wave is modified while propagating inland – by the processes of funnelling, resonance, amplification and damping – most often described in terms of shallow water tides (such as compound and overtides). Depending on the purposes and use, tidal symmetry/asymmetry, excursion, and residuals can be visualized and assessed in several different ways by plotting tidal currents – collected by propeller current meter and/or by applying ADCP (see Turbulence piece; and my 1998 Taylor & Francis paper) technology. Simultaneous time-series measurements of velocity vectors conducted at different depths (to show depth asymmetry and stratification) and at different locations (to show the pattern of tidal excursion and residuals) are useful. . . . Here are glimpses of some of the state-of-art tidal current portrayal techniques: One traditional method is to construct tidal ellipse (also known as hodograph) – in fact this was very popular before the beginning of digital processing (in particular those that apply MATLAB routines on ADCP measurements). Tidal ellipses are plotted by connecting the tip of radiating time-series current vectors (demeaned or actual) measured at a station. If demeaned, the ellipse closes – otherwise a residual exists in the direction of dominant motion – caused by asymmetry, wind-driven current and/or river current (particularly for those stations in the coastal ocean located at or near estuaries and river mouths). Apart from this, the plot immediately indicates at least 2 more important tidal behaviors: (1) the nature and alignment of tidal excursion; (2) the rotational direction of currents (clockwise in the northern hemisphere; G-G de Coriolis, 1792 – 1843). Tidal excursion alignment is bathymetry/topography controlled. In my dissertation, it is revealed for the first time that submarine canyons refract an incoming tidal wave – by acting as a conduit through which tide propagates faster than the surrounding area. In the Ganges Canyon – known as the Swatch of No Ground (a very deep canyon with muddy and steep slopes that collapse often, generating turbidity currents on the northern Bay of Bengal seafloor; the canyon supposedly formed during the last Ice Age low sea level stand, when the Ganges River debouched at this location), tidal excursion on two sides of the canyon shows such a distinct behavior – both in excursion pattern as well as in amplitudes. JM Coleman (1969) speculated the possibility of such an influence of the canyon. The phase relationship between tidal height and current can be portrayed by plotting both together. Progressive waves show in-phase or in sync relationship between height and current – while in standing waves the two are out-of-phase with currents preceding the height by about 90 degree (in purely standing waves). Coastal tides are a standing wave type oscillation. Stick diagrams of measured and smoothed tidal current vectors – when plotted together with tidal fluctuation, show the nature of changing incoming and outgoing current pattern – in time and over the depth. The changing pattern over the water-column is a showcase of whether or not stratification is present. Measurements in open-water could indicate the effects of wind driven surface current, and its magnitude and directional Coriolis transformation over the depth – often in portraying the existence of Ekman spiral (G-G de Coriolis, 1792 – 1843; FW-J Nansen, 1861 – 1930; VW Ekman, 1874 - 1954), if present. Frequency syntheses of tidal currents in magnitude and direction – done by presenting them in polar scatter diagrams, histograms of directional roses, and histograms combining the direction and speed – are useful. Transformational evolution of the tidal wave – can be assessed in cluster or group behaviors – when frequency diagrams of multiple stations are compared. Progressive vector diagrams are a good indicator of rotating tide, excursion direction and residuals. They are plotted by progressively connecting each time-series current vector. It is one of the most effective ways to indicate the trajectory fate of water particles or waterborne light contaminant particulates. In addition, when simultaneous measurements are available over the depth, the plot immediately indicates whether or not water column stratification is present. One way to show the strength of tidal currents in directional patterns is to decompose the time-series measurements into orthogonal Northings and Eastings. Such decomposed orthogonals are one more way to determine the residual current magnitudes and directions. Depending on location of measuring stations, the residuals are an indication of tidal asymmetry, wind-driven circulation and/or unidirectional riverine/estuarine currents. In my Ph. D. dissertation, I have presented a correlation diagram relating tidal energy (variance of the depth-mean tidal current amplitude) with tidal range – yielding a second degree polynomial between the two. It turns out that such a relationship is theoretically supported in tide dominated coastal waters. As an example, in a tide-dominated coastal water of 4 m tidal range (macro-tidal > 4 m), the expected peak depth-mean tidal current is 1.44 m/s. In terms of energy (with a water density of 1025 kg/m^3), this tide possesses a kinetic energy to the order of 2122 J/m^3 at the phase of peak current. . . . 3. 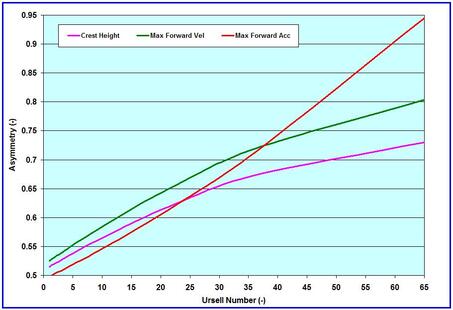The Short Wave The ubiquitous ocean surface waves (short wave, L/d < 20) are irregular, random and spectromatic – continuously churned, modified and re-modified by speeding wind at the air-water interface – and by bathymetry/topography at the seabed-water interface when waves start feeling the bottom (see Ocean Waves and Transformation of Waves). We have seen that, for all practical purposes, waves can be treated as linear or symmetric when U ≤ 5.0. At higher U, wave nonlinearity or asymmetry becomes important – because it causes asymmetrical horizontal forces on structures (see Wave Loads on Piles 2008 and Wave Forces on Slender Structures) and seabed – and leaves residuals in the direction of dominant motion. The discussed visualization and plotting methods for long waves can also be used – albeit in a different way – to assess the short wave asymmetry, and the degree of coherence/incoherence with other factors of the wave developing and sustenance systems. Some examples are: (1) wave height and period time-series together with that of wind speed stick diagrams; (2) wave height and period time-series with tide, and with seabreeze/landbreeze; (3) scatter diagram of wave parameters with wind speed; (4) scatter diagram of wave height vs wave period (see The World of Numbers and Chances); and (5) spectral analyses to assess the wave energy spectrum in frequency and direction domains. The effects of the length of fetch (see Wave Hindcasting to find out the expected relationships) can be assessed on wave height and period. Now, let us move on to describing a method on how to simply quantify wave asymmetry in terms of U. This is done for the example 1 meter high 8 second wave discussed in the Linear Waves and Nonlinear Waves pieces. In this illustration, the wave is followed to assess and estimate its evolving wave kinematics, from d = 20 m (U ≈ 1.0) to d = 3 m (U ≈ 65.3). It is assumed that the wave is incident on shore parallel smooth bathymetry (head-on) – therefore is not subjected to other transformational effects – such as refraction and diffraction. Note that the example wave of this height breaks roughly at d = 1.3 m. The focus is on the behavior of wave peak or crest – of crest height (CH), peak surface horizontal velocity (PSHV) and peak surface horizontal acceleration (PSHA). The primary motivation for focusing on peaks – is to ascertain the effects of wave asymmetries on the maximum forward heading surface horizontal drag and inertial forces on structures. The asymmetry factors of crest height (F_ch), PSHV (F_cv) and PSHA (F_ca) – are all defined with reference to (or with respect to) the summation of the absolute values of their crest and trough peaks. With this definition, symmetry = 0.5, crest amplification is > 0.5, and trough flattening or damping < 0.5. To make the derived asymmetry relations readily applicable, the reference summation amplitudes are determined by Linear Wave Theory – while the crest amplifications and trough damping, are determined by Nonlinear Wave Theory. This approach allows one to estimate asymmetry parameters in terms of simple linear wave theory and U. A plot of the derived relations for crest amplification asymmetry factors is presented in the attached image. The curves show how asymmetry (in crest height, maximum forward heading surface velocity, and maximum forward heading surface acceleration) amplifies nonlinearly as U increases. To better understand it, let us compare some numbers:
. . . Pull toward or push out? Interestingly, such a trivial matter has significance in the distinction of traditional cultural differences of peoples. Push-pull is same as the action-reaction-duo of a balancing system – but emphasis on one or the other has a special meaning. One simple example is the operation of a wood-slicer. In the West the slicing is done by pushing out, while in Japan – it is the opposite. Similar difference exists in the hand-saw operation. A Japanese scholar explained the difference like this: traditional attitude of accomplishing things in Asia is by pulling one toward, indicating the spirit of inclusiveness of harmonious living. In the West the practice evolved from a different motivation. Such a difference in attitudes must have developed and took shape over thousands of years – in the evolution and maturing of social thought processes. Perhaps a koan like this fits the piece: Do not manage things to create the difference wider and skewed. Try an alternative approach. . . . . . - by Dr. Dilip K. Barua, 25 September 2020
0 Comments
Leave a Reply. |
RSS Feed
