Breakwater

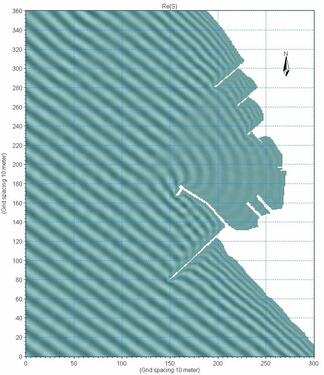Ever since the 1978 failure of a massive breakwater (BW) in Port Sines, Portugal – coastal engineers around the world went back to reviewing the BW design approaches and methods. During my studies at Delft in 1982 – the event and the possible lapses and causes of its failure – came for discussions again and again in coastal engineering lectures. The Sines Deepwater (~ 50 m) BW was designed and constructed of massive 42 tonne armor-layer dolos (dolos are pre-fab concrete units, designed to achieve good interlocks and stability when placed randomly – each unit has three stems, the central and the two twisted ones on ends) to withstand waves up to 100-year extreme of 11 m high significant wave (see Spectral Waves for definition). But near the end of the construction period – a storm that registered a lower wave height, dislodged about 2/3rds of the units – and some subsequent less powerful storms did the rest of the work by destroying the BW.
The risk of failure, the scale and cost of such massive structures – have generated renewed research interests in coastal labs around the world. Physical scale modeling tests – such as those in the massive Delta Flume in Emmeloord (the Netherlands), and in the CERC (Coastal Engineering Research Center) facilities in Vicksburg, Mississippi were some of the examples. The efforts resulted in the refinement of existing formulae and coefficients, and yielded new ones.
.  .  .
In this piece let us attempt to understand some interesting aspects of BW engineering. Engineering literature is full of materials on various aspects of BW planning, loading, stability, designs, and effects assessments. Among them, the following lists have most of the resources one needs for breakwater engineering: (1) Random Seas and Design of Maritime Structures (Y Goda 2000); the USACE (United States Army Corps of Engineers) (2) 1984 Shore Protection Manual (SPM); and its reincarnation, Coastal Engineering Manuals (CEM): (3) the 2002 CEM (EM 1110-2-1100 Part II; Chap 8 – Hydrodynamic Analysis and Design Conditions), (4) the 2006 CEM (EM 1110-2-1100 Part VI; Chap 5 – Fundamentals of Design, and Chap 6 – Reliability Based Design of Coastal Structures); (5) the 2007 Rock Manual (C683, the use of rock in hydraulic engineering, 2nd ed.) of EUROCODE, CIRIA (Construction Industry Research and Information Association) and CUR (Civil Engineering Research and Codes, the Netherlands); the JW Van der Meer publications, starting with his (6) 1988 Ph.D. Diss. (Rock slopes and gravel beaches under wave attack, Delft Univ. of Technology, the Netherlands, Delft Publication No. 396); and his (7) 1992 Delft Lecture Note, Conceptual Design of Rubble Mound Breakwaters; (8) RY Hudson 1958 (Design of quarry-stone cover layers of rubble-mound breakwaters, hydraulic laboratory investigation, Research Report 2-2, Waterways Experiment Station, Vicksburg, MS); and (9) R Iribarren 1938 (Una Formula Para el Calculo de los Digues de Escollera, Technical Report HE 116-295, University of California, Berkeley, CA). On 2D Wave Diffraction Modeling suite: (10) the 2005 Bouss-2D Wave Model in SMS, ERDC/CHL CHETN-I-69/70; (11) the 2007 Delft3D-Wave, TU Delft and Delft Hydraulics; and (12) the 2008 Waves Modules, DHI (Danish Hydraulic Institute). Different aspects of BW engineering are highly elaborate – I will briefly focus on some selected portions of them in simple terms. An overview of civil engineering works on our seashore (see Civil Engineering on our Seashore), and of barrier systems engineering (see Flood Barrier Systems) were posted earlier – that laid out some basics of coastal engineering (CE) works.
.  .  .
1. Breakwater Intro
A BW generally refers to an in-water self-standing coastal protection or defense structure – shore-attached, detached or offshore. It belongs to the Water Barrier group of structures (see Flood Barrier Systems) in coastal engineering; and may define a system when multiple BWs and functions are integrated together as a package. The purpose of a BW is to diffract, break and obstruct the continuity of an incoming wave – in order to create a tranquil or shadow zone of minimal or no wave activities behind it. Although the term is primarily applied to describe coastal protection or defense structures against wave attack, the underlying concept is similar – for example, in breaking the flow of a river current to protect an inland harbor or river bank erosion from current forcing (collectively known as river training structures). The functional properties of a BW are achieved by designing a suitable layout and dimension – the size of which falls into the definition of a large structure – with its dimension, D scaling with the local wave length, L such that D/L > 1/5 (see Wave Forces on Slender Structures). This means that a BW has a significant presence in the surrounding hydrodynamic field – in diffraction, deflection, reflection, transmission, absorption and scattering of waves, currents and alluvial sediment transports and dispersion. One important aspect of BW configuration – in terms of hydrodynamic loading – is the convergence and divergence of wave energies. The convergence – in particular, at the convex bends and at BW heads – implies that those places must be stronger than the rest of the structure to withstand amplified wave loading.
.  .  .
2. Breakwater Types and Functions
The necessity for a minimal wave zone can be varied – in port applications, the purpose is to create a harbor where vessels and ships (see Ship Motion and Mooring Restraints) can safely navigate in and out – and moor to load and unload cargoes and people. The second most important necessity is to protect a shore from wave erosion and beach degradation, or to prevent entry of unwanted sediments into a harbor. BWs are classified as two basic types: Floating and Fixed. Floating BWs are pontoons tethered in position either by guide piles, or by chains anchored to the seafloor. A pontoon acts as a deterrent of, or as a low-pass filter to the incident waves (mostly short-periods ~ 4 s) – with the additional use as a loading/unloading platform. They are mostly applied in low wave-climate areas to design marinas where small pleasure boats can be safely secured on several inside finger floats. Different aspects of this type of BW – incident wave attenuation efficiency and transmission are discussed in the Wave Structure Interactions & Scour piece. The primary focus of this piece is Fixed BW.
Breakwaters anchored to and founded on the seabed – as statically or dynamically stable hydraulic structure define a fixed BW. Depending on the scale of project and purpose, as well as on the prevailing hydrodynamic and wave climate, a fixed BW structure can be built by sheet pile walls, caissons (a concrete box or boxes filled with sand), rubble mounds, or combinations of them. Typically, caisson breakwaters can be a vertical face type, a composite type when the caisson sits on top of a raised platform built by rocks/rubbles, a perforated vertical face type (perforations eliminate wave reflection from the vertical wall), and armored caisson type (the seaside of the caisson is protected by rock armor units). Both sheet pile and caisson structures need quarry rock scour protection at seabed.
.  .  .
2.1 Fixed Breakwater
Fixed BW can be classified according to the magnitude of a Stability Number – defined as a ratio of wave height (H) to the product of armor unit relative density (Δ) and a characteristic dimension (D) of the unit or N_s = H/ΔD. When N_s ≤ 1, it falls into the category of a statically stable monolithic massive defense structure such as caissons and seawalls (in this case D is the height or width of the structure). All other structures including the rubble mounds and the shoreline itself are mostly dynamically stable with N_s > 1 (for rubble mounds, D = D_n50, the 50th percentile nominal rock diameter). In a dynamically stable structure, hydrodynamic forcing is assumed to cause profile changes in various degrees – with the displacements of rocks from a relatively unstable position to new stability. While this process goes on, the integrity of the structure remain largely unaffected or intact. However such structures succumb to failure – when large amounts of armor rocks are broken or are carried away exposing the underlayers and foundational core.
BWs can be designated into four vertical zones according to their exposure to the hydrodynamic loading. They are: the Zone I – the bottom foundational zone below the level of Mean Low Water (MLW); the Zone II – the tidal zone from MLW to the Mean High Water (MHW), loading on this zone is very frequent and determines the longterm structural stability; the Zone III – the higher high water zone from MHW to the design level, wave attack on this zone is less frequent but of high impact; and the top Zone IV subjected to the effects of runup and overtopping.
Shore perpendicular breakwaters attached to the shore are mostly conceived to serve beach management purposes. They are termed as Groins or Groin Systems, and have a range of typical shapes (Straight, T, Y, L, etc.) – the selection of which depend on the purpose and effectiveness. These types of breakwaters interrupt littoral transport, and attenuate the effects of onshore waves. They are usually low crested and are constructed of low-cost quarry rocks and runs. Literature and manuals suggest different planning approaches of such structures. For Groin Systems, the length of each unit is usually transitioned from short at the updrift side to the full length at the downdrift side. The spacing between each Groin usually scales with the length: the spacing is some 2 to 3 times the Groin length.
Shore parallel detached breakwaters – as a way to manage beach erosion and littoral transport – are often identified according to its location with respect to the shoreline. A parameter (L) defining a ratio of breakwater distance from the shoreline (X_off), and the 80% of surf zone width (S_80, note that about 80% of littoral transport occurs within the surf zone; see The Surf Zone processes), or L = X_off/S_80. When L ≤ 0.5, the breakwater is classified as a Beach BW (it protects the foreshore without significantly altering the littoral transport). A Coastal BW is defined when 0.5 < L ≤ 2.0 (intervenes the littoral transport to prevent beach erosion). At L > 2.0, it is known as Offshore BW. This type must be highly robust to withstand high waves and to interrupt and diffract incoming waves.
A fixed BW can also be classified according to the elevation of its crest from the still water level. In broad terms, two types can be identified: the emergent and the low crested breakwaters (LCB). The crest height of an emergent BW is usually high to prevent overtopping or to allow limited spray (breaking waves spray out into air) overtopping – and must take account of design storm surge height, wave set-up, wave run-up, height to compensate BW settlement and a freeboard on top of the design water level. If installed, the concrete cap of an emergent BW (usually used for utilitarian purposes) must be protected against overtopping damages by providing a crown wall. LCBs have various forms and heights depending on the desired limitations of overtopping – and the requirement to achieve certain wave attenuation goals. There are those that allow green overtopping (submerged BW acts as a weir transmitting a portion of the wave energy), and those that emerge and marginally submerge depending on the water level – thus allowing different categories of overtopping.
.  .  .
3. Diffracting Waves by Configuring the BW Layout
Diffraction is a process of bending the wave energy by obstructing its direct or head-on propagation. Waves lose a portion or all of its energy while bending from the illuminating zone to the shadows. Engineers use this property of wave behavior to design an area of low-energy wave environment so that vessels and ships can moor safely to load/unload cargoes and people – or to protect a shoreline from high energy wave actions and erosions. The ratio of diffracted (Hd) and incident (Hi) wave heights defines the diffraction coefficient, Cd = Hd/Hi.
Characterization of the incident hydrodynamic field in quantitative terms must begin with a clear qualitative understanding of the wave and sediment climate systems of the area. The a-group and b-group of activities shown in the coastal engineering envelope (see Civil Engineering on our Seashore) are the ones to start with. They include: use of longterm timeseries measurements from moored buoy or other platforms (in absence of such measurements, Wave Hindcasting techniques are used, if necessary based on Beaufort Wind Scale) together with analytical and physical and/or numerical modeling.
Before the times of digital computation and numerical modeling, engineers used diffraction diagrams and analytical models to determine diffracted wave heights. The Weigel (RL Weigel 1962) diffraction diagrams included in the SPMs and CEMs, and simple analytical models (Goda and others) are some examples. A simple illustration using the Goda relation, would show that an illuminating (a) 3-m, 8-sec head-on wave at 10-m water depth, would diffract to 0.34 m (Cd = 0.112) in the shadow zone at –60 deg (the direction refers to the direction of wave orthogonal approach).
Modeling activities search for an optimal layout that would diffract the incoming waves to a tolerable height or energy level behind the BW. Physical scale modeling is somewhat a thing of the past as it involves considerable efforts and cost (however massive projects often require it). In contrast, modern practices of optimizing the configuration of a BW layout mostly rely on numerical modeling. First, the regional wave climate is established by wave action modeling – that lays out the boundary conditions for the detailed modeling including the outlines for most probable forcing scenarios. The most effective way of detailed layout optimization is by Mild Slope or Boussinesq (French mathematician and physicist Joseph Valentin Boussinesq; 1842 – 1929) wave modeling – an example of such an application is shown in the attached image. I love the beauty of Boussinesq modeling approach – its phase-resolving capability to analyze the non-linear wave fields close to the shore, etc. I had the opportunity to use it in multiple occasions – the results of one such application are published in my Ports 2013 Conference paper. While the capabilities are real – there are also many limitations and constraints of what a numerical model can or cannot do – therefore one should be careful in interpretations of model results, and their uncertainties. Some aspects of these issues are outlined in the Water Modeling piece. For the sake of brevity, the rest of this piece will primarily focus on rubble mound BW and designing armor rock size.
.  .  .
4. Rubble Mound Breakwaters
Rubble mound breakwaters represent a triangular (trapezoidal to be exact with thick peak) prism with its base at the seabed and its triangular peak rising to a certain height above or below the still water level (SWL). The thickness of the peak is structurally required to have the dimension of 3 armor rock sizes, often equipped with a concrete cap and a seaside crown wall for an emergent BW. The advantage of a rubble mound is its capacity to absorb and dissipate the wave breaking energy – the dissipation is ensured by the porosity of armor layer.
It is a relatively cost-effective simple structure with the sides laid out in symmetric or asymmetric slope configuration. The slopes must be flatter than the rock angle of repose or internal friction (~ 1V:1.25H). In the case of an asymmetric triangle, the seaward side slope is usually flatter than the harbor side. Let us attempt to see some aspects of this structure in simple terms.
Stability of an Armor Unit. The crucial step in BW engineering is to address the stability of armor rocks or concrete units placed (randomly by dumping, or one-by-one in regular orders) on the rubble mound slope. The hydrodynamic loading of a breaking wave must be balanced by the armor unit weight resting on a slope and held in place by neighboring units and the foundational core. The loading is primarily caused by breaking wave drag and lift forces (inertial forces are negligible, see Wave Forces on Slender Structures). These forces translate to the wave height when breaking water particle velocities become a square root function of H (see Tsunami and Tsunami Forces). In essence, the dynamic stability of armor units depends on a multitude of factors – related to (a) Wave Forcing, (b) Rock Properties and (c) Structural Integrity. They are:

• Wave Forcing: (1a) water depth or elevation; (2a) water density (see Coastal Water); (3a) foreshore seabed slope; (4a) wave parameters (see Waves – Height, Period and Length); (5a) storm duration or number of waves; (6a) angle of wave attack; (7a) convergence or divergence of the wave field; and (8a) wave breaking type on the slope.
  
• Rock Properties: (9b) armor unit density, and strength and durability; and (10b) angularity or shape of the unit.
• Structural Integrity: (11c) angle of the BW slope; (12c) acceptable damage level or dislocation of units; (13c) permeability of the structure (note the porosity of randomly placed rough quarry rocks varies from 37 to 40%); and (14c) gradation and layering of the interiors rocks including the core, and the strengths and durability of them.
  

With dependence on so many variables and parameters, it becomes formidable to derive a straightforward formula. Engineers then had to resort to dimensional analysis technique to reduce the variables. This technique yields dimensionless numbers which can be related through laboratory tests and scale modeling. As pointed out earlier, one such number is the Stability Number, N_s = H/ΔD_n50. First breakthrough of finding a useful relation came from Iribarren (1938). He simply focused on non-breaking waves on the BW slope, and related N_s to the product of coefficient, a friction factor and BW slope factor. His investigations revealed something very interesting – that for a non-breaking wave, the downrush force dominates or is more than the uprush. His formula is only of academic interest – because it substantially underestimates the required armor rock size.
.  .  .
4.1 Hudson Formula (RY Hudson 1958)
The next breakthrough came from flume tests in the CERC lab facilities at Vicksburg, Mississippi. The derived relation, promoted by SPM manuals and has been in use for long time was the Hudson formula. It simply related N_s to the product of a stability coefficient and slope factor. The formula is based on flume tests relying on the actions of broken waves on non-overtopped permeable core BW slope. SPM manuals prescribed different applicabilities of this formula and provided different tabulated values of the stability coefficient. Although the formula was derived using regular waves, the manual prescribed to use significant wave height (Hs) in the 1977 manual – and changed it to the 10th percentile significant wave height (1.27Hs) in the 1984 manual and in subsequent CEM editions.
The limitations of this simple formula are often cited as: (1) probable scale-effects from small model tests; (2) use of regular wave loading only during testing; (3) the effects of wave period and storm duration not accounted for; (4) damage level is not well-defined; and (5) primarily meant for non-overtopped permeable core structure. However, to ensure wide applicability, all these limitations (as we shall see except the wave-period effect) are accounted for, and lumped into the stability coefficient. The example (a) broken wave, when acts on a 1V:2H BW slope, the 1977 formula yield a rough quarry rock armor unit mass of 4.5 tonne with no damage. It nearly doubles to 9.2 tonne when the 1984 formula is used.
.  .  .
4.2 Van der Meer Formula (JW Van der Meer 1988)
Van der Meer (VDM) for his PhD thesis conducted elaborate lab tests in the Delta Flume. His derived formula is more complex than Hudson’s. And N_s is related to additional factors – by taking into account of the effect of wave period, wave breaking type, permeability, damage level, and storm duration. VDM formula is tested for wave steepness from 0.005 to 0.06, and with the maximum wave numbers of 7500, at which the forces on the armor unit reach equilibrium (meaning that no more damages could occur with further increase in the number of waves).
Let us see how the VDM formula predicts rough quarry rock armor size for the example wave. The (a) wave breaks on the 1V:2H BW slope as a plunging breaker (see The Surf Zone). For 4000 waves on an impermeable core with no damage, the required VDM unit mass is 6.7 tonne (note that this size is smaller than what is required by the 1984 Hudson). If the wave period is increased to (b) 12-sec, the wave breaking type is still plunging, but then the mass increases to 12.7 tonne. For this particular wave forcing, it turns out that the Hudson 1984 formula is conservative for wave periods ≤ 9.7 sec. For heavy storms characterized by long period waves, the VDM formula is appropriate.
.  .  .
4.3 Materials and Other Aspects
As an alternative to quarry rock, engineers resorted to lab testing to develop different interlocking shapes of concrete units. In most cases, investigations leading to finding such units became necessary when suitable sizes of quarry rocks (most commonly used densities: rock 2.65 tonne/m^3; water 1.025 tonne/m^3; 1 tonne = 1000 kg) could not be identified and found for high wave climate areas – in cost-effectiveness, quantities, qualities and energy dissipation. Concrete units allow engineers to design steep slope (~ 1V:1.5H) rubble mounds, thus affording significant cost savings in relatively deep waters. The units are usually reinforced when the required mass of each unit is heavier than about 10 to 20 tonne (often constrained by the placing equipments and methods). Many countries have developed their own tested shapes, some common examples include (with the year and the countries of development): Tetrapod (France 1950), Tribar (USA 1958), Stabit (UK 1961), Tripod (the Netherlands 1962), Dolos (Republic of South Africa 1963), Seabee (Australia 1978), Accropode (France 1980), Shed (UK 1982), Core-loc (USA 1996), and Xbloc (the Netherlands 2003).
I like to stop at this by noting many other aspects of rubble mound BW engineering that accompany design specs. In brief they include:

• width of the crest: the specified minimum is some 3 to 4 times D_n50;
• the thickness of armor layer: minimum 2 layers, 2D_n50. Thicker armor layer ensures more porosity, therefore more energy dissipation but at a high cost. Concrete units have higher porosity (~ tetrapod 50%), therefore ensure more energy dissipation;
  
• the gradation of quarry rock armor units, the ranges are: narrow (D_85/D_15 < 1.5); wide (1.5 < D_85/D_15 < 2.5); and very wide (D_85/D_15 > 2.5);
  
• among the LCBs there are many options one can tap on: reef breakwater (dynamically stable mostly with permeable core that allow modulated wave transmission), the marginal LCBs that allow both green and spray overtopping, and the low LCBs, weir or sill whose crest remain mostly submerged. Overtopping and wave energy transmission allows smaller armor rocks than the non-overtopped BWs;
  
• a recent development in BW engineering is Berm Breakwater (BBW). BBW design takes advantage of forcing the waves to break before it reaches the main BW – by selecting a suitable height of the berm placed on the seaside slope. The berms of BBW are designed to have damages by taking most of the wave breaking load;
  
• many BW sections include a toe on the seaside. The toes have two functions – first one is to support the overlying rocks and the foundational underlayers and core – and the second is to take a portion of wave breaking load when waves break at or near the toe level. When the depth of the toe ≤ 0.5 times the water depth, the toe armor unit should have the same spec as that of the BW armor. For higher toe depths lower size toe armor can be used;
  
• for many other specs of the rubble mound BW structure including the gradation and filtration requirements of underlayers and core – the CEM and Rock Manual have elaborate guide materials. The rock gradation must satisfy three requirements: (1) stability, and prevention of (2) the loss of fines (3) and the development of pore pressure (by ensuring adequate permeability);
  
• Rock sizes and other specs of coastal protection ripraps or revetments are estimated using the similar methods as those of BWs;
  
• assessing the effects/impacts of BW systems on the local Fluid, Solid and Life systems, and;
  
• for BWs conceived of risky investments because of their high environmental and failure impacts – an advanced probabilistic analyses and design approach is often followed.
  

.  .  .
There we have it.
Perhaps some moments of thoughtful reflection and reckoning from all of us are useful – on something as miniscule as a microbe virus yet powerful enough to shatter the confidence in our protective capability of public health. And on something – that opened a terrible flaw in otherwise assumed as civilized systems and norms – but which in reality were nothing but artificial covers on the hidden wounds inflicted by many years of skewed socioeconomic policies promoting asymmetry and inequity. On top of that climate warming is heading towards unsustainable instabilities and trends; and information abuses and malicious internet viruses are at an alarming stage of threatening public security and privacy. With all these, it is no surprise to hear global calls – loud and clear, for the strengths of wisdom, mutual respect and unity.
.  .  .
With that, let me finish this piece with a Koan:
Nothing compares with the fury of jealousy, arrogance, anger and hatred – when built within the systems of power or is tolerated – it unleashes the ruthless monster of cruelty and brutality that burns everything it comes close to.

.  .  .  .  .

- by Dr. Dilip K. Barua, 19 June 2020

 

---