Science and technology
working with nature- civil and hydraulic engineering to aspects of real world problems in water and at the waterfront - within coastal environments
 Coastal inlets represent a hydrodynamic connection between two water bodies – the open coastal water on the one hand, and the inland sheltered water body, waterway or lagoon on the other. The name itself suggests that inlets are openings or discontinuities in the shoreline to let oceanic influences such as tide, wave, storm surge and tsunami to propagate inside. They are usually narrow channels that have been historically utilized to install bridges. Another historical significance is that pioneering explorers used the inlets to sail inside into harbors and upriver to discover new lands.
. . . 1. Inlet Types Four different types are usually distinguished – the geological, the hydrological, the human-made and the alluvial-tidal. The first represents a fixed-shore setting that has been formed during the geological processes – straits and many narrows in fjords are of this type. The second represents delta distributaries – the long outlets draining out the river flow into the ocean. In addition to describing them as Estuaries, hydrodynamics and morphological stabilities of this type are better treated as channels – mostly belonging to the deltaic processes discussed in the Coastal River Delta piece on the NATURE page. The third is a dredged-out channel connecting a closed water body to open water. In most cases, the purpose of opening of such an inlet is to develop marinas by facilitating navigation of pleasure boats to and from the marina. The fourth type, also known as the tidal inlet – is the natural response of sandy alluvium to establish a connection between the open coastal water and the inland lagoon. Mostly formed or cut during storm surges, they represent a discontinuity in the barrier island along many littoral shores. These inlets are usually a narrow waterway – its length scaling with width – typically varying from 1 to 5 times the width. Literature is full of materials discussing these types of inlets – their stability, sedimentation, navigation, and technical and economic management issues. . . . 2. Estuary - the Hydrological Inlet Before moving into discussing further, perhaps spending a little time to clarify the term ESTUARY – the hydrological inlet, would be useful. Let me try to do this based on my 1990 paper: In Search of the Definition of an Estuary published in the BD Journal of the Institution of Engineers. The estuary definition evolved through time starting from investigators like BH Ketchum (1951) and JC Dionne (1963) to the comprehensive syntheses of several papers compiled by the American Association for the Advancement of Science (1967) and the National Academy of Sciences (1977). Dionne’s definition focusing on the St. Lawrence Estuary divides an estuary length into: (1) a marine or lower estuary in free connection with the open sea, (2) a middle estuary subject to strong salt and fresh water mixing, and (3) an upper or fluvial estuary subject to daily tidal action. But the 1967 definition by DW Pritchard focusing primarily on Chesapeake Bay is mostly cited in literature: an estuary is a semi-enclosed coastal body of water which has a free connection with the open sea and within which sea water is measurably diluted with fresh water derived from land drainage. Three terms stand out in this definition: semi-enclosed body of coastal water, open-connection to sea, and measurable dilution. Compared to the Dionne suggestion, tide is excluded from this definition with the understanding that its role is primarily in mixing of waters. In addition the tidal arm of the fresh-water river reach is not considered as an estuary. An additional problem appears with this definition – that in most large river systems like the Amazon, the Ganges-Brahmaputra and the Mississippi, the measurable dilution occurs in open sea water during high river stages – outside their physical land boundary. Therefore according to the Pritchard definition such systems do not have an estuary during this time! In reality estuarial reaches translate back and forth in response to the strength of unidirectional fresh-water flow. To address this problem and by focusing to include large river systems, my suggested definition in the 1990 paper reads as: an estuary is either a semi-enclosed coastal body of water which has a free connection with the open sea or part of the open sea or both, within which sea water is measurably diluted with fresh water derived from land drainage. Basically then, an estuary is any open and/or semi-enclosed coastal water body, where sea water salinity is measurably diluted by fresh-water derived from land drainage. Moving on – some materials of this piece are based on my Ports2013 paper, presented at the conference in Seattle and published by ASCE: Integrated Modeling and Sedimentation Management: the Case of Salt Ponds Inlet and Harbor in Virginia. This particular inlet was human-made, dredged to develop a marina in parts of the Salt Ponds water body, and connect it to Chesapeake Bay. In this work, sedimentation problems of Salt Ponds Inlet were addressed by coupled numerical modeling {tide + wave + sediment transport + morphology} together with some analytical approaches – among others by comparing wave and tidal powers. . . . 3. Coastal Inlet Hydraulics Inlet opening, closure or its stability depend on four basic oceanic forcings: (1) regular tidal pumping, (2) wave actions and littoral sand mobilization, (3) episodic but seasonal storm actions, and (4) rarer but powerful tsunami events. The effects of the last two can hardly be overemphasized – in addition to cutting new inlets or closing the existing ones, they impose new boundary conditions that are reworked by the regular forces of tide and wave – to achieve new dynamic equilibrium. Sands are continuously mobilized at the mouth of a tidal inlet by cross-shore and longshore wave actions. If tidal actions do not have the ability to flush out the wave-mobilized sediments, an inlet is doomed to closure. Each year billions of dollars are spent across the world to dredge out sandy shoals of an inlet. The inland parameters influencing an inlet stability is the size of the lagoon, its inter-connection with other systems and the freshwater that drains into the lagoon. The last but not the least is the textural composition of the littoral material, and the amount of sediment loads. Perhaps discussing more of this topic in 3 groups would help streamlining the rest of this piece. . . . 3.1 Cross-sectional Stability of Tidal Inlets. Three easily identifiable features characterize an alluvial tidal inlet system – the ebb-tidal delta on the ocean end, the flood-tidal delta on the bay end, and a relatively narrow deep inlet channel in-between. There had been considerable interests in the cross-sectional stability of tidal inlets – starting from the beginning of 20th century {to name some investigators: LJ LeConte 1906; MP O’Brien (Morrough Parker O’Brien Jr., 1902 – 1988, considered father of coastal engineering) 1931; FF Escoffier 1940; P Bruun and F Gerritsen 1960; JW Johnson 1973; JT Jerrett 1976; MO Hayes 1980}. In its utmost simplicity, the stability was conceived as a simple behavioral model relating the measured inlet cross-sectional area to the tidal prism – as a central fitting, A = CP^n; with a coefficient C and an exponent n on the tidal prism P. Tidal prism is the volume of water an ocean tide forces through an inlet to fill the inland basin {the prism can either be estimated by integrating, for example the hourly-tidal-flows through an inlet for the window of rising tide – from trough to crest; or as a product of the inland basin area and the tidal height within the basin}. The coefficient and the exponent are adjustable and verifiable parameters and vary from inlets to inlets – but Jarrett’s analyses show that they are in the order of: C = 3.8*10^-5 to 7.5*10^-4; n = 0.86 to 1.03 in SI unit. They were determined {in general, the coefficient is high when the exponent is low; and vice versa} for all the measured jettied and unjettied inlets along the US coast. The simple, yet very insightful model have drawn many follow-up works. It turns out that such a relationship can be established for any tide dominated estuarial channels – e.g. the paper I have presented along with my good friend and mentor Fred Koch in 1986 {Characteristic morphological relationship for tide dominated channels of the lower Meghna estuary, UNESCO, BUET} shows such a possibility. The discussed tidal inlet cross-sectional stability model immediately indicates the following:
. . . 3.2 Inlet-Bay Hydraulics Despite providing a first-order understanding of the inlet stability and more, the reality of the problem is much more complex than the simple inlet cross-sectional stability formula. One way to appreciate this is to examine the one-dimensional Saint-Venant hydrodynamic equation applicable in long inlets (French mathematician Adhémar Jean Claude Barré de Saint-Venant, 1797 – 1886). This equation is only solvable by numerical modeling, but an analytical solution to the problem was offered by GH Keulegan (1951) and DB King (1974). This can be very useful to have an improved impression of the inlet current and the bay tidal response. To illustrate its application, an image is included showing the ocean tide, bay tide and cross-sectional current. It is applicable for: inlet length 5 km; inlet width 3 km; inlet depth 15 m; bay depth 10 m; bay area 300 million square meter; tidal period 12.42 hours; and tidal range 2 m. In this particular example, the bay tide is slightly amplified and lags behind the ocean tide. The illustrated example is only good for preliminary assessment. To better understand the complicated inlet-system processes – a coupled shallow-water numerical model may prove to be the best recourse – like the one described in my Ports2013 paper. Since opening of the Salt Ponds Inlet in 1979, the City of Hampton is required to dredge the inlet every 2 to 3 years to maintain its navigability. This frequency of recurring dredging is quite a burden and has not decreased despite the construction of jetties at the inlet mouth. Presented as a comparison of tide and wave powers – it turns out the tidal prism of the inlet is quite inadequate to flush out the sands mobilized by wave actions – active in the Chesapeake Bay. . . . 4. Managing Tidal Inlets on Littoral Shores The problem of such inlets primarily hinges upon keeping them functional, open and navigable – this is necessary because most large inlets cater to the needs of ports, harbors and marinas – for in-and-out sailing of different types of vessels. What issues must one look for sound management of such an inlet? Let me try to highlight some briefly. Requirement of the year-round navigable depth for the highest-draft vessel allowed to call on the port and marina (for deep-draft harbors > 4.6 m; for small-craft harbors ≤ 4.6 m; for marinas according to design specifications). If outer anchorage idling is allowed and available, then a vessel can take advantage of the high tide by riding on it. Maneuverability of the exiting and entering vessels – overall lengths and widths of the allowable vessel – and maximum currents and vortices within the inlet-bay system. Smaller vessels have low tolerance thresholds of such factors than the large ones. Hydrodynamic actions on the inlet – the tidal pumping (period, range, inlet-bay hydraulics of tidal amplification or attenuation, volume of fresh water inflow), the wave actions on the inlet mouth (wave height and period – their spectral and directional distributions and seasonality); and the frequency and magnitude of extreme events such as storm surge and tsunami. One can classify an inlet as high, medium or low energy inlet based on wave and tidal actions and powers. Textural composition of sediments, in particular in the ebb- and flood-tidal deltas, the inlet and the beach. And the amount of sand mobilized and transported by both longshore and cross-shore processes – their reworking by flood- and ebb-tidal flow. Ebb- and flood-tidal delta morphodynamics – their identifiable morphological patterns and causal relationships with the forcing hydrodynamic parameters. Morphodynamics of the scour holes that typically develop at the constriction and at the head of jetties and breakwaters. If jetties (these are shore-perpendicular structures made of rocks or sheet piles placed at the updrift and downdrift sides of the inlet) are planned to address the problem – then some new issues appear: (1) most often such structures interrupt the continuity of longshore sand transport – the interruption causes updrift sedimentation and downdrift erosion; (2) what should be their lengths (for example, longer updrift jetty than the downdrift one? and how far should they extend beyond the surf zone?) and height; (3) if sand bypassing (such as by mechanical measures – e.g. pump dredging) is considered to re-establish the continuity of longshore transport – a totally new evaluation and design is required; (4) should weir be installed on the updrift jetty to allow some sand to pass through – only to be collected from pits and sumps for downdrift replenishment; and (5) should the jetties be permeable to some extent, to let some sands to pass through, and implications. Examining the potentials and feasibility of series of groynes (shore-perpendicular) both at updrift and downdrift locations to train the beach morphodynamics such that the inlet will not be overwhelmed by longshore and onshore transports. Examining the potentials and feasibility of reducing the wave actions by installing submerged offshore reefs. Or by installing series of offshore breakwaters both at updrift and downdrift areas beyond the surf zone. If dredging is unavoidable either as a stand-alone measure or as a supporting activity to other measures – then it is important to streamline and customize it, so that recurring costs can be minimized. As usual this topic turned out to be another long piece in the WIDECANVAS. Without further adieu, let me finish it with a line of wisdom from Leo Tolstoy (1828 – 1910): there is no greatness where there is no simplicity, goodness and truth. . . . . . - by Dr. Dilip K. Barua, 16 March 2018
0 Comments
 One must have guessed what I intend to discuss in this piece. People are glued to numbers in one way or another – for the sake of brevity let us say, from the data on finance, social demography and income distribution – to the scientific water level, wave height and wind speed. People say there is strength in numbers. This statement is mostly made to indicate the power of majority. But another way to examine the effectiveness of this statement is like this: suppose Sam is defending himself by arguing very strongly in favor of something. If an observer makes a comment like this, well these are all good, but the numbers say otherwise. This single comment has the power to collapse the entire arguments carefully built by Sam (unless Sam is well-prepared and able to provide counter-punch), despite the fact that numerical generalizations are invariably associated with uncertainties. Uncertainty is simply the lack of surety or absolute confidence in something.
. . . 1. Numbers on an Uncertainty Paradigm While the numbers have such powers, one may want to know:
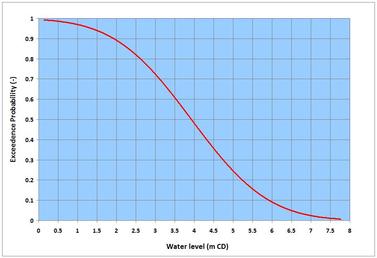
Probability with its root in logic is commonly known as probability distribution because it shows the distribution of a statistical data set – a listing of all the favorable outcomes, and how frequent they might occur (as a clarification of two commonly confused terms: probability refers to what is likely to happen – it denotes the surety of a happening but unsurety in the scale of its likelihood; while possibility refers to what might happen but is not certain to – it denotes the unsurety of a happening). Both of these methods aim at turning the information conveyed by numbers or data into knowledge – based on which inferences and decisions can be made. Statisticians rely on tools and methods to figure out the patterns and messages conveyed by numbers that may appear chaotic in ordinary views. The term many times originates from the Theory of Large Numbers. Statisticians say that if a coin is tossed for a short period, for instance 10 times – it may yield let us say, 7 heads (70% outcome) and 3 tails (30% outcome); but if tossed many more times, the outcomes of the two possibilities, head and tail is likely to be 50% each – the outcomes one logically expects to see. Following the proof of this observation by Swiss mathematician Jacob Bernoulli (1655 – 1705), the name of the theory was formally coined in 1837 by French mathematician Simeon Denis Poisson (1781 – 1840). There is a third aspect of statistics – it is known as the Statistical Mechanics (different from ordinary mechanics that deals with one single state) that is mostly used by physicists. Among others, the system deals with equilibrium and non-equilibrium processes, and Ergodicity (the hypothesis that the average over long time of a single state is same as the average of a statistical ensemble – an ensemble is the collection of various independent states). . . . 2. Random and Systematic Processes A few lines on the random and systematic processes. They can be discussed from the view points of both philosophical and technical angles. Randomness or lack of it, is all about perception – irrespective of what the numbers say, one may perceive certain numbers as random while others may see them differently. In technical terms, let me try to explain through a simple example. By building upon the Turbulence piece on the NATURE page, one can say that flow turbulent randomness appears when measurements tend to approximate to near-instantaneous sampling. Let us say, if one goes to the same spot again to measure turbulence under similar conditions; it is likely that the measurements would show different numbers. If the measurements are repeated again and again, a systematic pattern would likely emerge that could be traced to different causes – but the randomness and associated uncertainties of individual measurements would not disappear. Something more on the randomness. The famous Uncertainty Principle proposed by German theoretical physicist Werner Karl Heisenberg (1901 – 1976) in 1926 changed the way science looks at Nature. It broke the powerful deterministic paradigm of Newtonian (Isaac Newton, 1642 – 1727) physics. The principle says that there can be no certainty in the predictability of a real-world phenomenon. Apart from laying the foundation of Quantum Mechanics, this principle challenges all to have a close look at everything they study, model and predict. Among others, writing this piece is inspired after reading the books: A Brief History of Time (Bantam Books 1995) by British theoretical physicist Stephen Hawking (1942 - 2018); Struck by Lightning – the Curious World of Probabilities by JS Rosenthal (Harper Collins 2005); the 2016 National Academies Press volume: Attribution of Extreme Weather Events in the Context of Climate Change; and the Probability Theory – the Logic of Science by ET Jaynes (Cambridge University Press 2003). A different but relevant aspect of this topic – Uncertainty and Risk was posted earlier on this page indicating how decision making processes depend on shouldering the risks associated with statistical uncertainties. On some earlier pieces on the NATURE and SCIENCE & TECHNOLOGY pages, I have described two basic types of models – the behavioral and the process-based mathematical models – the deterministic tools that help one to analyze and predict diverse fluid dynamics processes. Statistical processes yield the third type of models – the stochastic or probabilistic models – these tools basically invite one to see what the numbers say to understand the processes and predict things on an uncertainty paradigm. While the first two types of models are based on central-fitting to obtain mean relations for certain parameters, the third type looks beyond the central-fitting to indicate the probability of other occurrences. . . . 3. Frequentist and Bayesian Statistics Before moving further, a distinction has to be made. What we have discussed so far is commonly known as the classical or Frequentist Statistics (given that all outcomes are equally likely, it is the number of favorable outcomes of an event divided by the total outcomes). Another approach known as the Bayesian Statistics was proposed by Thomas Bayes (1701 – 1761) – developed further and refined by French mathematician Pierre-Simon Laplace (1749 – 1827). Essentially, this approach is based on the general probability principles of association and conditionality. Bayesian statisticians assume and use a known or expected probability distribution to overcome, for instance, the difficulties associated with the problems of small sampling durations. It is like infusing an intuition (prior information or knowledge) into the science of presently sampled numbers. [If one thinks about it, the system is nothing new – we do it all the time in non-statistical opinions and judgments.] While the system can be advantageous and allows great flexibility, it also has room for manipulation in influencing or factoring frequentist statistical information (that comes with confidence qualifiers) in one way or another. . . . 4. History of Statistics Perhaps a little bit of history is desirable. Dating back from ancient times, the concept of statistics existed in all different cultures as a means of administering subjects and armed forces, and for tax collection. The term however appeared in the 18th century Europe as a systematic collection of demographic and economic data for better management of state affairs. It took more than a century for scientists to formally accept the method. The reason for such a long gap is that scientists were somewhat skeptical about the reliability of scattered information conveyed by random numbers. They were more keen on robust and deterministic aspects of repeatability and replicability of experiments and methods that are integral to empirical science. Additionally, scientists were not used to trust numbers that did not accompany the fundamental processes causing them. Therefore, it is often argued that statistics is not an exact science. Without going into the details on such arguments, it can be safely said that many branches of science including physics and mathematics (built upon theories, and systematic uncertainties associated with assumptions and approximations) also do not pass the exactitude (if one still believes this term) of science. In any case as scientists joined, statistical methods received a big boost in sophistication, application and expansion (from simple descriptive statistics to many more advanced aspects that are continually being refined and expanded). Today statistics represents a major discipline in Natural and social sciences; and many decision processes and inferences are unthinkable without the messages conveyed or the knowledge generated by the science of numbers and chances. However, statistically generalized numbers do not necessarily tell the whole story, for instance when it comes down to human and social management – because human mind and personality cannot simply be treated by a rigid number. Moreover, unlike the methods scientists and engineers apply, for instance, to assess the consequences and risks of Natural Hazards on vulnerable infrastructure – statistics-based social decisions and policies are often biased toward favoring the mean quantities or majorities at the cost of sacrificing the interests of vulnerable sections of the social fabric. When one reads the report generated by statisticians at the 2013 Statistical Sciences Workshop (Statistics and Science – a Report of London Workshop on the Future of Statistical Sciences) participated by several international statistical societies, one realizes the enormity of this discipline encompassing all branches of Natural and social sciences. Engineering and applied science are greatly enriched by this science of numbers and chances. . . . 5. Probability and Statistical Distributions In many applied science and engineering practices, a different problem occurs – that is how to attribute and estimate the function parameters for fitting a distribution in order to extrapolate the observed frequency (tail ends of the long-term sample frequencies, to be more specific) to predict the probability of an extreme event (which may not have occurred yet). The applied techniques for such fittings to a distribution (ends up being different shapes of exponential asymptotes) of measurements are known as the extremal probability distribution methods. They generally fall into a group known as the Generalized Extreme Value (GEV) distribution – and depending on the values of location, scale and shape parameters, they are referred to as Type I (or Gumbel distribution, German mathematician Emil Julius Gumbel, 1891 – 1966), Type II (or Fisher-Tippett distribution, British statisticians Ronald Aylmer Fisher, 1890 – 1962 and Leonard Henry Caleb Tippett, 1902 – 1985) and Type III (or Weibull distribution, Swedish engineer Ernst Hjalmar Waloddi Weibull, 1887 – 1979). This in itself is a lengthy topic – hope to come back to it at some other time. For now, I have included an image I worked on, showing the probability of exceedence of water levels measured at Prince Rupert in British Columbia. From this image, one can read for example, that a water level of 3.5 m CD (Chart Datum refers to bathymetric vertical datum) will be exceeded for 60% of time (or that water levels will be higher than this value for 60% of time, and lower for 40%). In extreme probability distribution it is common practice to refer to an event in recurrence intervals or return periods. This interval in years says that an event of a certain return period has the annual probability – reciprocal of that period (given that the sampling refers to annual maxima or minima). For example, in a given year, a 100-year event has 1-in-100 chance (or 1%) of occurring. Another distinction in statistical variables is very important – this is the difference between continuous and discrete random variables. Let me try to briefly clarify it by citing some examples. The continuous random variable is like water level – this parameter changes and has many probabilities or chances of occurring from 0 (exceptionally unlikely) to 1 (virtually certain). In many cases, this type of variables can be described by Gaussian (German mathematician Carl Freidrich Gauss, 1777 – 1855) or Normal Distribution. The discrete random variable is like episodic earthquake or tsunami events – which are sparse and do not follow the rules of continuity, and can best be described by Poisson Distribution. . . . 6. Making Sense of Numbers When one assembles huge amounts data, there are some first few steps one can do to understand them. Many of these are described in one way or another in different text books – I am tempted to provide a brief highlight here.
Before finishing I like to illustrate a case of conditional probability, applied to specify the joint distribution of wave height and period. These two wave properties are statistically inclusive and dependent; and coastal scientists and engineers usually present them in joint frequency tables. As an example, the joint frequency of the wave data collected by the Halibut Bank Buoy in British Columbia shows that 0.25-0.5 m; 7-8 s waves occur for 0.15% of the time. As for conditional occurrence of these two parameters, analysis would show that the probability of 7-8 s waves is likely 0.52% given the occurrence of 0.25-0.5 m waves; and that of 0.25-0.5 m waves is likely 15.2% given the occurrence of 7-8 s waves. This piece ended up into a long one than I anticipated. . . . Here is a piece of caution stated by a 19th century British statesman, Benjamin Disraeli (1804 – 1881): There are three kinds of lies: lies, damned lies, and statistics. Apart from bootstrapping, lies are ploys designed to take advantages by deliberately manipulating and distorting facts. The statistics of Natural sciences are less likely to qualify for lies – although they may be marred with uncertainties resulting from human error, data collection techniques and methods (for example, the data collected in the historic past were crude and sparse, therefore more uncertain than those collected in modern times). Data of various disciplines of social sciences, on the other hand are highly fluid in terms of sampling focus, size, duration and methods, in data-weighing, or in the processes of statistical analyses and inferences. Perhaps that is the reason why the statistical assessments of the same socio-political-economic phenomena by two different countries hardly agree, despite the fact that national statistical bodies are supposedly independent of any influence or bias. Perhaps such an impression of statistics was one more compelling reason for statistical societies to lay down professional ethics guidelines (e.g. International Statistics Institute; American Statistical Society). . . . . . - by Dr. Dilip K. Barua, 19 January 2018  I like to begin this piece with a line from Socrates (469 – 399 BCE) who said: I am the wisest man alive, for I know one thing, and that is that I know nothing. This is a philosophical statement developed out of deep realization – neither practical nor useful in the mundane hustle-bustle of daily lives and economic processes. Philosophers tend to see the world differently sometimes beyond ordinary comprehension – but something a society looks upon to move forward in the right direction. Scientists and engineers – for that matter any investigator, who explores deep into something, comes across this type of feeling nonetheless – the feeling that there appear more questions than definitive answers. This implies that our scientific knowledge is only perfect to the extent of a workable explanation or solution supported by assumptions and approximations – but in reality suffers from transience embedded with uncertainties. This piece is nothing about it – but an interesting aspect of actions and reactions between waves and structures.
. . . 1. Conservation of Wave Energy One of the keys to understanding these processes – for that matter any dynamic equilibrium of fluid flow – is to envision the principle of the conservation of energy – that the incident wave energy must be balanced by the structural responses – the processes of dissipation, reflection and transmission. These interaction processes cause vortices around the structure scouring the seabed and undermining its stability. Let me share all these aspects in a nutshell. As done in other pieces – I will provide some numbers to give an idea what we are talking about. The materials covered in this piece are based on my experience in different projects; and on the materials described in: the Random Seas and Design of Maritime Structures (Y. Goda 2000); the 2002 Technical Report on Wave Run-up and Wave Overtopping at Dikes (The Netherlands); the 2006 USACE Coastal Engineering Manual (EM 1110-2-1100 Part VI); the 2007 Eurotop Wave Overtopping of Sea Defences and Related Structures (EUROCODE Institutes); the 2007 Rock Manual of EUROCODE, CIRIA (Construction Industry Research and Information Association) and CUR (Civil Engineering Research and Codes, the Netherlands); and others. Most of the findings and formulations in wave-structure interactions and scour are empirical – which in this context means that they were derived from experimental and physical scale modeling tests and observations in controlled laboratory conditions – relying on a technique known as the dimensional analysis of variables. Although they capture the first order processes correctly, in real world problems the formulation coefficients may require judgmental interpretations of some sort to reflect the actual field conditions. Some materials relevant for this piece were covered earlier in the NATURE and SCIENCE & TECHNOLOGY pages. This topic can be very elaborate – and to manage it to a reasonable length, I will limit it to discussing some selected aspects of:
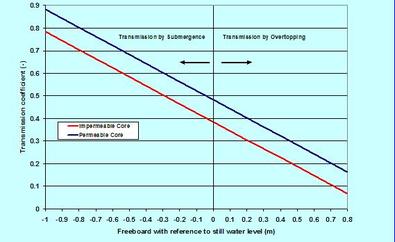
. . . 2. Wave Structure Interactions What must one look for to describe the wave-structure interactions? Perhaps the first is to realize that only the waves with lengths (L) less than about 5 times the structures dimension (D) are poised to cause wave-structure interactions (see the Wave Forces on Slender Structures on this page) in the presence of slender structures. The second is that the wave energy must remain in balance – which translates to the fact that sum of squares of the wave heights (H^2) in dissipation, reflection and transmission must add to the incident wave height squared. This balancing is usually presented in terms of coefficients (the ratios of dissipated, reflected and transmitted wave heights to the incident wave height), squares of which (C^2) must add to one. The third is the Surf Similarity Number (SSN, discussed in The Surf Zone on this page) – this parameter appears in every relation where a sloping structure is involved – it is directly proportional to wave period and slope. The fourth is the direction of wave forcing relative to the loading face of the structure – its importance can simply be understood from the differences in interactions between the head-on and oblique waves. Importance of other structural parameters will surface as we move on to discussing the processes. . . . 2.1 Wave Reflection Wave reflection can be a real problem for harbors lined with vertical-face seawalls. It can cause unwanted oscillation and disturbance in vessel maneuvering and motion, and in the scouring of protective structure foundations. As one can expect, wave reflection from a vertical-face smooth structure is higher than and different from a non-overtopped sloping structure. A non-breaking head-on wave on a smooth vertical-face structure is likely to reflect back straight into the incident waves – an example of perfect reflection. When waves are incident at an angle on such a structure, the direction of the reflected waves follows the principle of optical geometry. For sloping structures, the reflection is directly proportional to SSN, and it can be better grasped from a relation proposed by Postma (1989). Let us see it through an example. A 1-m high wave with periods of 6-s and 15-s, propagating head-on, on a non-overtopped 2 to 1 straight sloping stone breakwater (with a smooth surface and an impermeable core) would produce reflected waves in the order of 0.36 m and 0.83 m, respectively. When the slope is very rough built by quarried rock, most of the incident energies are likely to be absorbed by the structure. It is relevant to point out that according to Goda (2000), natural sandy beaches reflect back some 0.25% to 4% of incident wave energies. . . . 2.2 Wave Runup Wave runup is an interesting phenomenon – we see it each time we are on the beach – not to speak of the huge runups that occur during a tsunami overwhelming us in awe and shock. The runup is a way for waves to dissipate its excess energy after breaking. Different relations proposed in literature show its dependence on wave height and period, the angle of wave incidence, beach or structure slope – and on the geometry, porosity and roughness. A careful rearrangement of different proposed equations would indicate that the runup as directly and linearly proportional to wave period and slope, but somewhat weakly to wave height. This is the reason why the runup of a swell is higher than a lower-period sea – or why a flatter slope is likely to have less runup than a steeper one – or why the tsunami runup is so huge. An estimate following the USACE-EM would show that the maximum runups on a 10 to 1 foreshore beach slope are 1.9 m and 3.8 m for a 1-m high wave with periods of 6-s and 15-s, respectively. The explanation of the runup behavior is that the longer the wave period, the less is its loss of energy during breaking, affording the runup process to carry more residual energy. Although a runup depends on its parent oscillatory waves for energy, its hydrodynamics is translatory, dominated by the laws of free surface flows – this means in simple terms – the physics of the steady Bernoulli (Daniel Bernoulli; 1700 – 1782) equation. . . . 2.3 Wave Transmission How does the wave transmissions over and through a maritime structural obstacle work? Such structural obstacles are called breakwaters because they block or attenuate wave effects in order to protect the areas behind them. There are two basic types – the fixed or rigid, and the floating breakwaters. The former is usually built as a thin-walled sheet pile, a caisson or as a sloped rubble-mound (built by quarried rocks or other manufactured shapes). The second, moored to seabed or fixed to vertical mono-piles, is usually built by floats with or without keels. The floating breakwaters are only effective in a coastal environment of relatively calm short period waves (the threshold maximum ≈ 4 s) – because long period waves tend to transmit easily with negligible loss of energy. The attenuation capacity of such breakwaters is often enhanced by a catamaran type system by joining two floats together. First let us have a glimpse of wave transmissions over a submerged and overtopped fixed breakwater. To illustrate this over a low-crested (structure crest height near the still water level – somewhat higher and lower) rubble-mound breakwater, an image is included showing the transmission coefficients (ratio of transmitted to incident wave height) for a head-on 1-m high 6-s wave, incident on the 2 to 1 slope of a breakwater with a crest width of 1 m. This is based on a relation proposed by researches at Delft (d’Angremond and others 1996) and shows that with other factors remaining constant, the transmission coefficient is linearly but inversely proportional to the freeboard. For both the permeable and impermeable cores, the image shows the high transmission by submergence (often termed as green overtopping) and low transmission by overtopping – with the permeable core affording more transmissions than a non-permeable one. Emergent and submergent with the changing tide level, such transmissions are directly proportional to wave height, period and stoss-side breakwater slope, but inversely proportional to the breakwater crest width. Wave transmission concept over a submerged breakwater is used to design artificial reefs to attenuate wave effects on an eroding beach. In another application, the reef layout and configuration are positioned and designed in such a way that wave focusing is stimulated. The focused waves are then led to shoal to a high steepness suitable for surfing – giving the name artificial surfing reef. The transmissions through a floating breakwater are complicated – more for loosely moored than a rigidly moored. As a rule of thumb, an effective floating breakwater requires a width more than half the wave length, or a draft at least half the water depth. To give an idea, an estimate would show that for a 1-m high, 4-s head-on incident wave on a single float with a width of 2 m and a draft of 2 m – rigidly moored at 5 m water-depth – the transmitted wave height immediately behind would be 0.55 m. If the draft is increased to 2.5 m by providing a keel, the transmitted wave heights would reduce to 0.45 m. The estimates are based on Weigel (1960), Muir Wood and Fleming (1981), Kriebel and Bollmann (1996) and Cox and others (1998). . . . 2.4 Wave Overtopping Wave overtopping is a serious problem for the waterfront seawalls installed for protecting urban and recreational areas from high storm waves. It disrupts normal activities and traffic flow, damages infrastructure and causes erosion. Among the various researches conducted on this topic, the Owen (1982) works at the HR Wallingford shows some insights into the overtopping discharge rates. Overtopping discharge rate is directly proportional to the incident wave height and period, but inversely to the freeboard (the height of the structure crest above still water level). To give an idea: for a 1 m high freeboard, 2 to 1 sloped structure – a 1-m high wave with periods of 6-s and 15-s would have an overtopping discharge of 0.10 and 0.82 m^2/s per meter width of the crest, respectively. If the freeboard is lowered to 0.5 m, the same waves will cause overtopping of 0.26 and 1.25 m^2/s/m. . . . 2.5 Scour Scouring of erodible seabed in the vicinity and around a structure results from the obstruction of a structure to fluid flows. The obstructed energy finds its way in downward vertical motions – in the nearfield vigorous actions and vortices scooping out sediments from the seabed. Scouring processes are fundamentally different from the erosion processes – the latter is a farfield phenomenon and occurs due to shearing actions. The closest analogies of the two processes are like this: the vortex scouring action is like a wind tornado – while the process of erosion is like the ground-parallel wind speed picking up and blowing sand. Most coastal scours occur in front of a vertical sea wall, near the toe of a sloping structure, at the head of a breakwater, around a pile, and underneath a seabed pipe. They are usually characterized by the maximum depth of scour (an important parameter indicating the undermining extent of scouring), and the maximum peripheral extent of scouring action. It turns out that these two scouring dimensions scale with wave height, wave period, water depth and structural diameter or width. These parameters are lumped into a dimensionless number known as the Keulegan-Carpenter (KC) Number (a ratio of the product of wave period and nearbed wave orbital velocity to the structure dimension), proposed by GH Keulegan and LH Carpentar (1958). This number was introduced in the Wave Forces on Slender Structures piece on this page. Experimental investigations by Sumer and Fredsøe (1998) indicate that a scour hole around a vertical pile develops only when KC > 6. At this value, wave drag starts to influence the structure adding to the inertial force, and scouring action continues to increase exponentially as the KC and structure diameter increase. Scour prevention is mostly implemented by providing stone ripraps – of suitable size, gradation and filter layering. . . . The Koan of this piece: If you do not respect others – how can you expect the same from them. . . . . . - by Dr. Dilip K. Barua, 20 October 2017 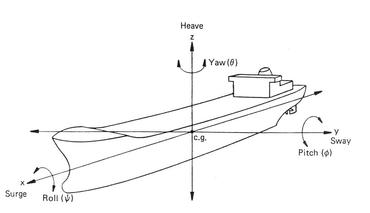 This topic represents one of the most interesting problems for port terminal installations – or in a broader sense for station keeping or tethering of floating bodies such as a ship (vessel) or a floating offshore structure. The professionals like Naval Architects and some Maritime Hydraulic Civil Engineers are trained to handle this problem. I had the opportunity to work on some projects that required the static force equilibrium analysis for low frequency horizontal motions, and the dynamic motion analysis accounting for the first order motions in all degrees of freedom. They were accomplished through modeling efforts to configure terminal and mooring layouts, and to estimate restraining forces on mooring lines and fenders for developing their specifications. Let me share some elements of this interesting topic in simple terms. To manage this piece to a reasonable length - some other aspects of ship mooring such as its impacts on structures during berthing are not covered. Hope to get back to this and other aspects at some other time.
This piece can appear highly technical, so I ask the general readers to bear with me as we go through it. It is primarily based on materials described by American Petroleum Institute (API), Oil Companies International Marine Forum (OCIMF), The World Association for Waterborne Transport Infrastructure (PIANC), British Standard (BS), the pioneering works of JH Vugts (TU Delft 1970) and JN Newman (MIT press 1977), and others. Imagine an un-tethered rigid body floating in water agitated by current, wave and wind. These three environmental parameters will try to impose some motions on the body – the magnitudes of which will depend on the strength and frequency of the forcing parameters – as well as on the inertia of the body resisting the motion and on the strength of restoring forces or stiffness. Before moving into discussing the motions further, a few words on current, wave and wind are necessary. Some of these environmental characteristics were covered in different pieces posted on the NATURE and SCIENCE & TECHNOLOGY pages. Among these three, currents caused by long-waves such as tide, are assumed steady because their time-scales are much longer than the ship motions. Both wave and wind, on the other hand are unsteady – and spectromatic in frequency and direction – causing motions in high (short period) to low (long period) frequency categories. In terms of actions, the ship areas below the water line are exposed to current and wave actions – for wind action it is the areas above the water line. Often the individual environmental forcing on the ship’s beam (normal to the ship’s long axis) proves to dominate the directional loading scenario. But an advanced analysis of the three parameters is required in order to characterize them as the combined actions from the perspectives of operational and tolerance limits – and for design loads acting on different loading faces of the ship. The acceptable motion limits vary among ships accounting for shipboard cargo handling equipment and safe working conditions. . . . 1. Rigid Body Oscillation and Natural Period Some simple briefs on the oscillation dynamics. When a rigid body elastic system is forced to displace from its equilibrium position, it oscillates in an attempt to balance the forces of excitation and restoration. The simplest examples are: the case of vertical displacement when a mass is hanged by a spring, and the case of angular displacement of a body fixed to a pivot. When the forcing excitation is stopped after the initial input, an elastic body oscillates freely in exponentially diminishing amplitude and frequency. A forced oscillation occurs when the forcing continues to excite the system – in such cases resonance could occur. The natural frequency (or reciprocally the period) of a system is its property and depends on its inertial resistance to motion, and on its strength to restoring it to equilibrium. The best way to visualize it is to let the body float freely in undamped oscillations. It turns out that the natural period is directly proportional to its size or its displaced water mass. This means that a larger body has a longer natural period of oscillation than a smaller one. Understanding the natural period is very important because if the excitation coincides with the natural period, resonance occurs causing unmanageable amplification of forces. In reality however, resonance rarely occurs because most systems are damped to some extent. Damping reduces the oscillation amplitude of a body by absorbing the imparted energy – partially (under-damped), or more than necessary (over-damped), or just enough to cause critical damping. Most floating systems are under-damped. Force analysis of an over-damped body requires an approach different from the motion analysis. . . . 2. Some Basic Ship Terms Here are some relevant terms describing a ship. A ship is described by its center-line length at the waterline (L), beam or width B (the midship width at the waterline), the draft D (the height between the waterline and ship’s keel), the underkeel clearance (the gap between the ship’s keel and the seabed), the fully loaded Displacement Tonnage (DT) – accounting for displacement of the ship with DWT (Dead Weight Tonnage – the displaced mass of water at the vessel’s carrying capacity – accounting for cargo, fuel, water, crew [including passengers if any] and food item storage), and the Lightweight (empty) Weight Tonnage (LWT). A vessel is known as a ship when its tonnage DWT is 500 or more. The ship dimensions are related to one another in some fashion allowing to making estimates of others if one is known. A term known as the block coefficient (CB) represents the fullness of the ship – it is the ratio of the ship’s actual displaced volume and its prismatic or block volume (with L, B and D). The typical CBs are 0.85 for a tanker and 0.6 for a ferry. To give an idea, the new Panamax vessel (maximum allowed through the new Panama Canal Lock) is L = 366 m; B = 49 m, and D = 15 m. Different classification societies like ABS (American Bureau of Shipping) and LR (Lloyd’s Register of Shipping) set the technical standards for the construction and operation of ships and offshore floating structures. . . . 3. Motion Degrees of Freedom What are some of the basic rigid body motion characteristics? The floating body motions occur in six degrees of freedom representing linear translational and rotational movements. Literature describes the six motion types in different ways; perhaps a description relying on the vessel’s axes is a better way of visualizing them. All the three axes – the horizontal x-axis along the length, the horizontal y-axis across the width, and the vertical z-axis originate at the center of gravity (cg) of the vessel. To illustrate them I have included a generic image (credit: anon) showing the motions referring to:
. . . 4. Inclination and Stability Another important understanding needs to be cleared. This is about the stability or equilibrium of the vessel for inclinational motions. A floating body is stable, when its centers of gravity (cg) and buoyancy (cb) lie on the same vertical plane. When this configuration is disturbed by environmental exciting forces like wind and wave, or by mechanical processes like imbalanced loading and unloading operations, the vessel becomes unstable shifting the positions of cg and cb. The imbalanced loading can only be restored to equilibrium by the vessel operators by re-arranging the cargo. Among others, the vessel operators also have the critical responsibility to leave the berth during a storm, to tending the mooring lines – so that all the mooring lines share the imposed loads – and in keeping the ship within the berthing limit. For non-inclinational motions like surge, sway, heave and yaw the coincidental positions of the cg and cb are not disturbed. They just translate back and forth in surge, and near and far in sway oscillations. In heave and yaw, the coincidental positions of cg and cb do not translate – for heave it is the vertical up and down motion, and for yaw it is the angular translatory motion about the vertical axis. . . . 5. Motion Analyses How to describe these motions and the corresponding forces in mathematical terms? The description as an equation is conceived in analogous with the equilibrium principle of a spring-mass system – where an oscillating exciting force causes acceleration, velocity and translation of the floating body. For each of the six degrees of freedom, an equation can be formed totaling six equations of motion. With all the six degrees of freedom active, the problem becomes very formidable to solve analytically; the only option then is to resort to numerical modeling technique. Motion analyses are conducted by two different approaches – the Frequency Domain analysis focuses on motions in different frequencies, adding them together as a linear superposition. The Time Domain analysis on the other hand focuses on motions caused by the time-series of the exciting parameters. Perhaps some more clarifications of the terms – the mass including the added mass, the damping and the stiffness – are helpful. The total mass (kg) of a floating body comprises of the mass of water displaced by it, and the mass of the surrounding water called the added mass – which is proportional to the size of the body, and also depends on different motion types. These two masses resist the acceleration of the body. The Damping (N.s/m; Newton = measure of force; s = time, second; m = distance, meter) is a measure of the absorption of the imparted energy by the floating system – having the effect of exponentially reducing its oscillation. Damping is three basic types: damping by viscous action, wave drift motion and mooring system restraining. The stiffness (N/m) is the force required of an elastic body to restore it to the equilibrium position. The terms discussed above refer to rectilinear motions of surge, sway and heave. How about the terms for angular motions of roll, pitch and yaw? The total mass for angular motions becomes the mass moment of inertia, and the stiffness is replaced by the righting moment (moment is the product of force and its distance from the center). In the cases of environmental and passing vessel excitations, gravity and mooring restraints try to restore the stability of the vessel. The roles of these restoring elements are like this:
A few words on the passing vessel effect. A speeding vessel passing past a moored vessel causes surge and sway loads and yaw moment on the latter. The magnitudes of them depend on the speed of the passing vessel, the distance between the two, and the underkeel clearance of the moored vessel. As a simple explanation involving the ships in a parallel setting: a moored vessel starts to feel the effect when the passing vessel appears at about twice the length of the former, and the effect (push-pull in changing magnitude and phase) continues until cleared of this passing away distance. Analysis shows that sway pull-out is the highest when the passing vessel is at the midship of the moored vessel – but the surge and the yaw are the lowest at this position. . . . 6. Mooring and Station Keeping Well so far so good. On some aspects of mooring now. Mooring or station keeping comprises of two basic types – fleet and fixed moorings. The former refers to systems that use primarily the tension members such as ropes and wires, and is mostly applied in designated port offshore anchorage areas. Ports have designated outer single-point anchorage areas where ships can wait for the availability of port berthing, and/or for loading from a feeder vessel and unloading to a lighterage vessel. The area is also used to remain on anchor or on engine-power during a storm. Ships can cast anchors in those areas or moor to an anchorage buoy. For a single point mooring on anchor a large mooring circle is needed to prevent the anchored ship from colliding with the neighbouring vessels. Assuming very negligible drifting of the anchor, the radius of this influence-circle depends on water depth, anchor-chain catenary and ship’s overall length. Anchoring to a moored buoy by a hawser reduces this radius of influence-circle of the moored ship. Buoy facilities are usually placed offshore for mooring of tankers, and such buoys are equipped with multiple cables and hoses to cater to the logistical needs of the vessel as well as for loading and unloading petroleum. A vessel moored at a single point is free to swing or weather-vane following the prevailing weather and current to align itself bow-on. The weather vaning is advantageous because it minimizes the vessel area exposed to wind, wave and current loads. Fixed Mooring refers to a system that uses both tension (ropes and wires) and compression members (energy absorbing fenders). A different type of fixed mooring, mostly implemented in rather calm environmental settings of current and wave is implemented in marinas. The floats of marinas are usually anchored via collars to vertical mono-piles. Only a single-degree of freedom is provided in this system – which means that the floats move rather freely vertically up and down with changing water levels. Typical fixed moorings include tying the ship at piers (port structures extending into the water from the shore), wharves (port structures on the shore), and dolphins (isolated fixed structures in water) together with loading platforms. The latter is mostly placed in deepwater by configuring the alignment such that moored ships will largely be able to avoid beam seas, currents and wind. The tying is implemented by wires and ropes – some are led from the ship winches through fair leads to the tying facilities like bollards, bitts or cleats on the berthing structures. Wires and ropes are specified in terms of diameter, material, type of weaving and the minimum breaking load (MBL). The safe working load (SWL) is usually taken as a fraction of MBL - some 0.5 MBL or lower. The mooring lines are spread out (symmetrically about the midship) at certain horizontal and vertical angles. Typically, the spring lines (closed to midship mostly resisting the longitudinal motions) spread out at an angle no more 10 degrees from the x-axis; the breasting lines (between spring and bow/stern lines, mostly resisting the lateral motions) spread out at an angle no more than 15 degrees from the y-axis; and the bow and stern lines are usually laid out at 45 degrees. The maximum vertical line angles are kept within 25 degrees from the horizontal. The key considerations for laying out mooring lines are to keep spring lines as parallel as possible; and breast lines as perpendicular as possible to the ship’s long axis. When large ships are moored with wires, a synthetic tail is attached to them to provide enough elasticity to the vessel motions. . . . This piece ended up longer than I anticipated. Let me finish it by quoting Nikola Tesla (1856 – 1943) – the famous inventor, engineer and physicist: If you want to know the secrets of the universe, think in terms of energy, frequency and vibration. . . . . . - by Dr. Dilip K. Barua, 15 September 2017 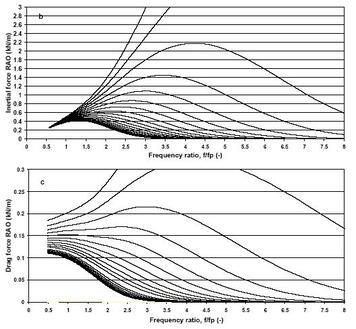 Most of the materials in this piece are based on my 2008 ISOPE (International Society of Offshore and Polar Engineers) paper: Wave Loads on Piles – Spectral Versus Monochromatic Approach. This paper discusses, for both monochromatic and spectral waves, how the Morison forces (Morison and others, 1950) compare for a surface piercing round vertical pile in some cases of waves with Ursell Numbers (Fritz Joseph Ursell, 1923 – 2012), U in the order of 5.0. I have included an image (courtesy ISOPE) from this paper showing inertial and drag force RAOs as a function of frequency. The RAO or Response Amplitude Operator represents the maximum force for a unit wave height.
. . . 1. Slender In-water Structures Standing in the nearshore water of unbroken waves, one experiences a shoreward push when a wave crest passes and a seaward pull when a wave trough passes – and if the waves happen to be large he or she may experience dislodging from the foothold. The immediate instinct is to recognize the power of a wave in exerting forces on members standing on its way – resisting its motion. How to estimate these forces? Do structures of all different sizes experience the same type of forces? The answer to the first question depends on how well one answers the second question – how the structure sizes up with the wave – the wave length (L) to be exact. It turns out that the nature of wave forces on a structure can be distinguished based on the value of a parameter known as the diffraction parameter – a ratio of the structure dimension (D) perpendicular to the direction of wave advance, and the local wave length, L. When D is less than about 1/5th of L, the structure can be treated as slender and wave forces can be determined by the Morison equation. . . . 2. Hydrodynamics of Morison Forces In this piece let us attempt to see how the Morison forces work – how the forces apply in considerations of both monochromatic and spectral waves. I will also touch upon the nonlinear wave forces. Slender structures exist in many port and offshore installations as vertical structures – as mono pile and pile-supported wharfs in ports – as gravity platforms and jacket structures in offshore structures – and as horizontal structural members and pipelines. What are the Morison forces? They are the forces caused by the wave water particle kinematics – the velocity and acceleration. The two kinematics causing in-line drag and inertial horizontal forces are hyperbolically distributed over the height of a vertical standing structure – decreasing from the surface to the bottom. For a horizontal pipeline, the loads include both the in-line horizontal forces as well as the hydrodynamic vertical lift force. More about these to-and-fro wave forces? The drag force is due to the difference in the velocity heads between the stoss and lee sides of the structure; and the inertial force is due to its resistance to water particle acceleration. The hydrodynamic lift force is due to the difference in flow velocities between the top and bottom of a horizontal structure. I will attempt to talk more about it at some other time. Do the slender members change the forcing wave character? Well while the structures provide the resistances by taking the forces upon themselves; they are not able to change the character of the wave – because they are too small to do so. From the perspectives of structural configuration, when a vertical member is anchored to the ground but free at the top, it behaves like a cantilever beam subjected to the hyperbolically distributed oscillating horizontal load. When rigid at both ends, the member acts like a fixed beam. For a horizontal pipeline supported by ballasts or other rigidities at certain intervals, it also acts like a fixed beam with the equally distributed horizontal drag and inertial forces and the vertical hydrodynamic lift forces. . . . 2.1 Forces in Linear Waves Before entering into the complications of spectral and nonlinear waves, let us first attempt to clarify our understanding of how linear wave forces work. We have seen in the Linear Waves piece on the NATURE page that the wave water particle orbital velocity is proportional to the wave height H, but inversely proportional to the wave period T. The water particle acceleration is similarly proportional to H, but inversely proportional to T^2. The nature of proportionality immediately tells us that waves of low steepness (H/L) have lower orbital velocities and accelerations – therefore they are able to cause less forces than the waves of high steepness. For symmetric or linear waves, the orbital velocity and acceleration are out of phase by 90 degrees. In the light of Bernoulli Theorem (Daniel Bernoulli, 1700 – 1782) dealing with the dynamic pressure and velocity head, the drag force is proportional to the velocity squared. Both the drag and inertial forces must be multiplied by some coefficients to account for the structural shape and for viscosity of water motion at and around the object. Many investigators devoted their times to find the appropriate values of drag and inertia coefficients. A book authored by T. Sarpkaya and M. Isaacson published in 1981 has summarized many different aspects of these coefficients. Among others the coefficients depend on the value of Reynolds Number (Osborne Reynolds, 1842 – 1912) – a ratio of the product of orbital velocity and structure dimension to the kinematic viscosity. The dependence of the forces on the Reynolds Number suggests that a thin viscous sublayer develops around the structure – and for this reason the Morison forces are also termed as viscous forces. The higher the value of the Reynolds Number, the lower are the values of the coefficients. The highest drag and inertial coefficients are in the range of 1.2 and 2.5, respectively, but drag coefficients as high as 2.0 have been suggested for tsunami forces. . . . 2.1.1 Importance Indicators of Drag and Inertial Forces How do the drag and inertial forces compare to each other? Two different dimensionless parameters answer the question. The first is known as Keulegan-Carpenter (G.H. Keulegan and L.H. Carpenter, 1958) Number KC; it is directly proportional to the product of wave orbital velocity and period and inversely proportional to the structure dimension. It turns out that when KC > 25 – drag force dominates, and when KC < 5 inertia force dominates. The other factor is known as the Iversen Modulus (H.W. Iversen and R. Balent, 1951) IM, is a ratio of the maximums of inertia and drag forces. It can be shown that both of these two parameters are related to each other in terms of the force coefficients. While the horizontal Morison force is meant to result from the phase addition of the drag and inertial forces, which are 90 degrees out of phase, the conventional engineering practice ignores this scientific fact, instead adds the maximums of the two together. This practice adds a hidden factor of safety (HFS) in design forces. For example, a 2-meter, 12-second wave acting on a 1-meter vertical structure standing at 20-meter of depth (U = 6.4) would afford a HFS of 1.45. However HFS varies considerably with the changing values of IM – with the highest occurring at IM = 1.0, but decreases to unity at very high and low values of IM. . . . 2.2 Forces in Non-linear Waves How does the wave nonlinearity affect the Morison forces? We have seen in the Nonlinear Waves piece on the NATURE page that the phase difference between the velocity and acceleration shifts away from 90 degree – with the increasing crest water particle velocity and acceleration. For the sake of simplicity, let us focus on a 1-meter high 8-second wave, propagating from the region of symmetry at 10 meter water depth (U = 5.0) to the region of asymmetry at 5 meter water depth (U = 22.6). By defining and developing a relationship between velocity and acceleration with U, it can be shown the maximum linear and nonlinear forces are nearly equal to each other at U = 5.0. But as the wave enters into the region of U = 22.6, the nonlinear drag force becomes 36% higher than the linear drag force. The nonlinear inertia force becomes 8% higher than the linear one. With waves becoming more nonlinear in shallower water, the percentage increases manifold higher than the ones estimated by the linear method. While the discussed method provides some insights on the behaviors of nonlinear Morison forces, USACE (US Army Corps of Engineers) CEM (Coastal Engineering Manual) and SPM (Shore Protection Manual) have developed graphical methods to help estimating the nonlinear forces. . . . 2.3 Forces in Spectral Waves Now let us turn our attention to the most difficult part of the problem. What happens to the Morison forces in spectral waves? How do they compare with the monochromatic forces? To answer the questions, I will depend on my ISOPE paper. The presented images from this paper shows the inertial and drag force RAOs over the 20-meter water depth at 1-meter interval from the surface to the bottom – for a 2-meter high 12-second wave acting on a 1-meter diameter round surface-piercing vertical pile. The forcing spectral wave is characterized by JONSWAP (Joint North Sea Wave Project) spectrum (see Wave Hindcasting). For this case, the RAOs are the highest at frequencies about 3.5 times higher than the peak frequency (fp) of 0.08 Hertz (or 12-second). This is interesting because the finding is contrary to the general intuition that wave forces are high at the frequency of the peak energy – the period effects on wave kinematics! As the frequency decreases, the inertial force RAO diminishes tending to zero. The drag force RAO, on the other hand, tends to reach a constant magnitude as the frequency decreases. This finding confirms that at low frequency motions of tide and tsunami, the dominating force is the drag force (which is also true for cases when KC > 25.0). How do the spectral wave forces compare with the monochromatic wave forces? It turns out that for the case considered, the monochromatic method underestimates the wave forces by about 9%. A low difference of this order of magnitude is good news because one can avoid the rigors of the spectral method to overcome such a small difference – the difference of this magnitude is in the range of typical uncertainties of many parameters. . . . . . - by Dr. Dilip K. Barua, 17 November 2016 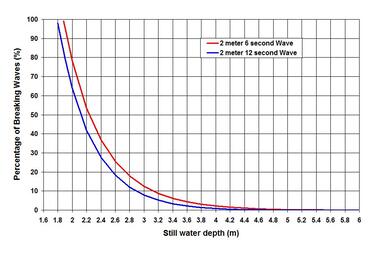 We have talked about the Natural waves in four blogs – Ocean Waves, Linear Waves, Nonlinear Waves and Spectral Waves on the NATURE page, and in the Transformation of Waves piece on the SCIENCE & TECHNOLOGY page. In this piece let us turn our attention to the most dynamic and perhaps the least understood region of wave processes – the surf zone – the zone where waves dump their energies giving births to something else.
1. The Surf Zone What is the surf zone? The Surf zone is the shoreline region from the seaward limit of initial wave breaking to the shoreward limit of still water level. The extent of this zone shifts continuously – to shoreward during high tide and to seaward during low tide – to shoreward during low waves and to seaward during high waves. The wave breaking leading to the transformation – from the near oscillatory wave motion to the near translatory wave bores – is the fundamental process in this zone. Note that by the time a deep-water spectral wave arrives at the seaward limit of the surf zone, its parent spectrum has already evolved to something different, and the individual waves have become mostly asymmetric or nonlinear. In the process of breaking a wave dumps its energy giving birth to several responses – from the reformation of broken waves, wave setup and runup, and infragravity waves – to the longshore, cross-shore and rip currents – to the sediment transports and morphological changes of alluvial shores. The occurrence, non-occurrence or extents of these responses depends on many factors. It is impossible to treat all these processes in this short piece. Therefore I intend to focus on some fundamentals of the surf zone processes - the processes of wave breaking and energy dissipation. . . . 2. Characterizing the Processes How are the surf zone processes treated in mathematical terms? Two different methods are usually applied to treat the problem. The first is based on the approximation of the Navier-Stokes (French engineer Claude-Louis Navier, 1785 – 1836; and British mathematician George Gabriel Stokes, 1819 – 1903) equation. In one application, it is based on the assumption that the convective acceleration is balanced by the in-body pressure gradient force, wave forcing and lateral mixing, and by surface wind forcing and bottom frictional dissipation. The second approach is based on balancing two lump terms – the incoming wave energy and the dissipated energy. We have seen in the Linear Waves piece on the NATURE page that wave energy density is proportional to the wave height squared. In a similar fashion, the dissipated wave energy is proportional to the breaking wave height squared multiplied by some coefficients. Both the approaches are highly dependent on the empirical descriptions of these coefficients – making the mathematical treatment of the problem rather weak. . . . 2.1 Energy Dissipation Let us focus on the energy approach – how the breaking energy dissipation occurs in the surf zone. Many investigators were involved in formulating this phenomenon. For individual monochromatic waves, the two most well-knowns are: the one proposed by M.J.F. Stive in 1984 and the other one proposed by W.R. Dally, R.G. Dean and R.A. Dalrymple in 1985. It was the energy dissipation formulation by J.A. Battjes and J.P.F.M. Janssen in 1978 that addressed the energy dissipation processes of spectral waves. This formulation required an iterative process, and was therefore cumbersome to apply. However with the modern computing power, that hurdle does not exist any more. In addition to the aforementioned investigators, there are many others who modified and refined the formulations and understandings of the surf zone processes. In this piece let us attempt to see how the energy dissipation works for spectral waves. Among the coefficients influencing the energy dissipation is a factor that defines how fractions of the spectral wave group break. This factor is very important, and let my try to illustrate how that works – by solving the term iteratively. . . . 2.2 Wave Breaking - the Surf Similarity Number Before doing that let me highlight some other understandings of the surf zone processes. Early investigators of the surf zone processes have noticed some important wave breaking behaviors – that all waves do not break in the same fashion and on all different beach types. Their findings led them to define an important dimensionless parameter – the Surf Similarity Number (SSN) – also known as the Iribarren Number (after the Spanish engineer Ramon Cavanillas Iribarren, 1900 – 1967; C.R. Iribarren and C. Nogales, 1949) – or simply the Wave Breaking Number. This number is the product of beach slope and wave steepness – and is directly proportional to the beach slope and inversely proportional to the square root of wave steepness (steepness is the ratio of wave height and wave length – long-period swells are less steep than short-period seas). Either of these two parameters could define a breaker type. To identify the different breaker types it is necessary to define some threshold SSN values. Among the firsts to define the threshold values were C.J. Galvin (1968) and J.A. Battjes (1974), but more lights were shed by many other investigators later. On the lower side, when the SSN is less than 0.5, the type is termed as Spilling Breaker – it typically occurs on gently sloping shores during breaking of high-steepness waves – and is characterized by breaking waves cascading down shoreward creating foamy water surface. On the upper side, when the SSN is higher than 3.3, the type changes to Surging and Collapsing Breakers. In a surging breaker, waves remain poorly broken while surging up the shore. In a collapsing breaker, the shoreward water surface collapses on the unstable and breaking wave crest. Both of these breakers typically occur in steep shores during periods of incoming low-steepness waves. When the SSN ranges between 0.5 and 3.3, the type becomes a Plunging Breaker – it typically occurs on intermediate shore types and wave steepness – and is characterized by curling of shoreward wave crest plunging and splashing on to the wave base. This type of breaker causes high turbulence, and sediment resuspension and transport on alluvial shores. An example of sediment transport processes and associated uncertainties in the surfzone is in the Longshort Sand Transport. . . . 2.3 Quantifying the Breaking Waves Perhaps it is helpful if we think more for a while, of what happens in the surf zone – as one watches the incoming waves – high and low – breaking at different depths propagating on to the shore. What prompts wave breaking? The shallow water wave-to-wave interaction – Triad lets wave spectrum evolve into a narrow band shifting the peak energy to high frequencies. The concentration of wave energies lets a wave-form to become highly nonlinear and unsustainable as the water particle velocity exceeds the celerity (square root of the product of acceleration due to gravity and depth), and right before breaking it takes the shape of a solitary wave (a wave that does not have a definable trough). I have tried to throw some lights on this breaking process in my short article published in the 2008 ASCE Journal of Waterway, Port, Coastal and Ocean Engineering {Discussion of ‘Maximum Fluid Forces in the Tsunami Runup Zone’}. Further, we have discussed in the Transformation of Waves piece on this page that a wave cannot sustain itself when it reaches the steepness at the threshold value of 1/7 and higher. A criterion proposed by Miche [Le pouvoir reflechissant des ouvrages maritimes exposes a l’action de la houle. 1951] captures the wave breaking thresholds not only due to the limiting steepness, but also due to the limiting water depths in shoaling water. In 1891, J. McCowan has shown that wave breaks when its height reaches 4/5th of the water depth on flat bottom. Now that we know the wave breaking types and initiation, let us try to understand how the energies brought in by the waves are dissipated. To illustrate the process I have included an image showing the percentage of fractional energy dissipation, as two spectral waves – a 2-meter 6-second and a 2-meter 12-second – propagate on to the shore. As demonstrated in the image, spectral waves begin to lose energy long before the final breaking episode happens. This means that the transformation process lets the maximums of the propagating spectrum to break as they reach the breaking threshold. In addition, as expected the shorter period waves (see the 6-second red line) lose more energy on way to the shallow water than the longer period (see the 12-second blue line) ones. By the final breaking, all the energies are dissipated giving births to other processes (water level change, nearshore currents and sediment transport). On a 1 to 10 nearshore slope, the SSN for the two cases are 0.5 and 1.1, respectively – indicating a Plunging Breaker type – but at two different scales. On most typical sandy shores, the long period waves are more likely to end up being a Plunging Breaker than the short-period ones. At the final stage, the breaking wave heights are 76% and 79% of water depths for the two cases. . . . Does anyone see another very important conclusion from this exercise? Well this conclusion is that, for any given depth and wave height the long-period waves bring in more energy to the shore than the shorter ones – the period effect. Let us attempt to see more of it at some other time. Some more insights on the surf zone waves are provided by Goda (Yoshima Goda, 1935 – 2012) describing a graphical method to help determine wave height evolution in the surf zone. His graphs show, for different wave steepness and nearshore slopes, how the maximum and the significant wave heights evolve on way from the deep water to the final breaking – and then to the reformed waves after final breaking. . . . . . - by Dr. Dilip K. Barua, 10 November 2016  In this piece let us talk about another of Ocean’s Fury – the Storm Surge. A storm surge is the combined effects of wind setup, wave setup and inverse barometric rise of water level (the phenomenon of reciprocal rise in water level in response to atmospheric pressure drop). Also important in the surge effects is tide because the devastating disasters occur mostly when the peak surge rides on high tide (the superimposition of tide and storm surge is known as storm tide).
1. Storm Surge Intro The wind setups as a minor contributor to water level rise occur in most coastal water bodies during the periods of Strong Breeze (22 – 27 knot; 1 knot = 1.15 miles/h; 1.85 km/h; 0.51 m/s) and Gale Force (28 – 64 knot) winds (see Beaufort Wind Scale) – during winter storms and landward monsoons – and are measurable when the predicted tide is separated from the measured water levels. Such setups and seiche (standing wave-type basin oscillation responding to different forcing and disturbances) are visible in water level records of many British Columbia tide gauges. Storms are accompanied by high wave activities, consequently wave setups are caused by breaking waves. Wave setup is the super elevation of the mean water level – this elevation rises from the low set-down at the wave breaker line. Let us attempt to understand all these different aspects of a storm surge – but focusing only on Hurricane (wind speed > 64 knot) scale storms. I have touched upon the phenomenon of storm surge in the Ocean Waves piece on the NATURE page telling about my encounter with the 1985 cyclonic storm surge on Bangladesh coast. Later my responsibilities led me to study and model some storm surges – surges caused by Hurricane ISABELLE (CAT-2, September 18, 2003), Hurricanes FRANCES (CAT-2, September 5, 2004) and JEANNE (CAT-3, September 26, 2004), Hurricane IKE (CAT-2, September 12, 2008) on the U.S. coasts. Some materials of my U.S. experiences are presented and published (Littoral Shoreline Change in the Presence of Hardbottom – Approaches, Constraints and Integrated Modeling, FSBPA 2009; Sand Placement Design on a Sand Starved Clay Shore at Sargent Beach, Texas, ASBPA 2010 [presented by one of my young colleagues at Coastal Tech]; and Integrated Modeling and Sedimentation Management: the Case of Salt Ponds Inlet and Harbor in Virginia, Proceedings of the Ports 2013 Conference, ASCE). In response to managing the storm effects, many storm prone coastal countries have customized modeling and study tools to forecast and assess storm hazard aftermaths. The examples are the FEMA numerical modeling tool SLOSH (Sea Lake and Overland Surges and Hurricanes) and GIS based hazard effects analysis tool HAZUS (Hazards U.S.). The SLOSH is a coupled atmospheric-hydrodynamic model developed by the National Hurricane Center (NHC) at NOAA. The model does not include storm waves and wave effects as well as rain flooding. NHC manages a Hurricane database HURDAT to facilitate studies by individuals and organizations. WMO-1076 is an excellent guide on storm surge forecasting. . . . 2. The Genesis of Wind Storms What are the characteristics of such a Natural hazard – of the storm surge generating Hurricanes? The Hurricanes (in the Americas), Cyclones (in South, Southeast Asia and Australia) or Typhoons (in East Asia) are a tropical low pressure system fed by spiraling winds and clouds converging toward the low pressure. Perhaps an outline of some of the key characteristics will suffice for this piece.
Before going further an important puzzle needs to be highlighted. Both the short wave and the long storm surge wave are generated by the dynamic pressure or kinetic energy exerted by the speeding wind; and their magnitudes are proportional to the square of the speed (referring again to Daniel Bernoulli, 1700 – 1782). Why are there two different wave types? What are the processes responsible for their formations? The questions may sound naive, but the answers may reveal some valuable insights. The short wave is the water surface response to transporting the gained energy in progressive wave motions. Like the turbulent wind, these waves are highly irregular and spectral. The storm surge waves, on the other hand result from the hydrodynamic balance between the wind-induced water motion and the resistance of that motion by the coast. The result is the piling up of water at the coast – a standing long wave. One should not forget however that the transformation aspects of a long wave – the processes of funneling, resonance (note that a storm surge is not monochromatic, therefore some frequencies may resonate to the basin natural frequency) and shoaling also play a role. These processes affect the storm surge height in wide continental shelves and in closed basins, and are discussed in the Tsunami and Tsunami Forces piece on this page. To illustrate the storm surge, I have included an image of the CAT-1 Hurricane SANDY (October 29, 2012) storm surge on the New Jersey coast. . . . 4. Storm Surge To manage this discussion into a short piece let us focus on a CAT-2 Hurricane characterized by a wind speed of 90 knot and a eye pressure of 970 millibar. Let us attempt to estimate some orders of magnitude of inverse barometric effect, wind setup and wave setup. Inverse barometric effect is often simplistically estimated as: 1 centimeter rise of water level in response to 1 millibar of pressure drop. For the example storm, the pressure drop at the center of the eye is 30 millibar – resulting in a reciprocal water level rise of 30 centimeter. This rise is rather like a moving dome of water having a typical diameter of some 30 kilometer. As one can imagine this simple estimate, however small that may be, cannot be added directly to the wind and wave setups because these two effects occur at the eye wall where wind speed is the highest. How does the wind setup occur? Sustained winds cause a water surface drift current in the direction of the wind. For the example CAT-2 Hurricane, the surface drift current in absence of an obstruction would be about 1.4 meter per second. For a landfalling Hurricane, when the shoreward surface-layer current is obstructed by the coast, water level rises at the coast to balance and cause a seaward bottom-layer current (the generated bottom current erodes and transports sediments seaward changing the morphology of the coastal sea). A simple estimate shows that the example CAT-2 Hurricane would cause a wind setup of 2.7 meter for a 50 kilometer wide continental shelf with an average water depth of 10 meter. To give an idea of the wave setup let us consider a maximum significant wave height of 4.0 meter, and a maximum wave period of 14 second (these parameters roughly corresponds to those measured during Hurricanes FRANCES and JEANNE near the coast). An estimate shows that the wave setup is about 1.2 meter, about 30% of the wave height. In aggregate the storm surge for the example CAT-2 Hurricane is in the order of some 3 meter – likely less in some areas and more in others. The Hurricanes FRANCES, JEANNE, IKE and ISABELLE registered surge height of about 2.0 meter in some places. What is the periodic scale of a storm surge? For the slow moving Hurricanes like FRANCES and JEANNE, it was about 4 days (from the time of rising to the time falling at the same water level), and for Hurricane IKE it was 1.5 days. Note that the periodic scale of this size covers 2 or more tidal cycles – but the damages mostly occur when the surge peak coincides with high tide (even more so when coincides with spring tide). . . . The complicacy of storm surges can best be described by numerical modeling. But it is also possible to estimate the surge more elaborately as a function of distance and time. Apart from damages, structural destruction and dike overtopping and breaches, storm surges greatly change nearshore and beach morphology providing works for summertime waves to reshuffle and redefine them. What we have discussed so far is positive storm surge that occurs on the right side of a landfalling Hurricane in the Northern Hemisphere. A negative storm surge, popularly known as the Sea Level Blow Out – also occurs simultaneously on the left side. See more in the Frontal Wave Force Field in Force Fields in a Coastal System. Examples of negative storm surge were vivid in emptying of Tampa Bay, Florida – during the storm episodes of 2017 Hurricane Irma, 2022 Hurricane Ian and 2024 Hurricane Milton. We have discussed about the likelihood of enhanced storm activity with Warming Climate on the NATURE page and also on this page. The high storminess together with the accelerated Sea Level Rise is only inviting humans to realize the consequences of our actions and face Nature’s Wrath – perhaps to a degree that modern humans have not witnessed before. When I started this piece, I thought of writing it as a small one. Instead, I ended up spending more time on this, resulting in the usual 4 to 5 pages length. Well what can one do when materials are overwhelming? . . . . . - by Dr. Dilip K. Barua, 3 November 2016  I have touched upon some of the extreme episodes in the Nature’s Action piece on the NATURE page. Tsunami is one of these Nature’s violent wraths that unleash immense trail of casualty and destruction on its path. Our memory is still fresh with the viciousness of havoc of the 2004 and 2011 tsunamis in Indonesia and Japan. Many of us have seen the live coverage of the 2011 Japan tsunami, and I have included a snapshot image (credit: anon) of it. Perhaps an image of this kind has given rise to the myth of Noah’s Ark in the ancient past. It is impossible for one not to realize the absolute shock and horror unless one is present on a tsunami scene. Let us try to talk about this interesting topic – tsunami characteristics and the loads they exert on structures standing on its path.
. . . 1. Tsunami Intro Tsunami is one of the rarest natural phenomena that occur with little definitive advanced notices. Tsunamis are caused by earthquake, landslide, volcanic eruption, and by rapid and high drop in atmospheric pressure. Perhaps talking about the first two will suffice for this piece. The first type triggered by underwater earthquakes – often called tsunamigenic earthquakes – causes sudden substantial rupture of the Earth’s crust displacing huge mass of water. The process gives birth to a series of impulsive waves known as tsunami that radiates out directionally from the source. Aspects of tsunamis generated by underwater volcanic eruption – in particular in light of the most recent violent eruption of Tonga on 15 January 2022 – remind us how devastating their effects could be. Tonga eruption is estimated to have measured 6 on the 1 to 8 VEI scale (Volcanic Eruption Index, C Newhall and S Self 1982). The eruption prompted Pacific wide tsunami warning – and really impacted Chile and Peru at more that 10,000 km away. On top of that, record books illustrate the largest and most disastrous tsunami generated by the Indonesian Krakatoa eruption on 27 August 1883 – it is said the tsunami was as high as 40 m – and together with the eruption killed some 36,000 people. A first order simplistic estimate of tsunami height (trough to crest) and the period (time interval between the two successive crests or troughs) relates these two tsunami parameters logarithmically to the magnitude of earthquake in the Richter scale. For example, a submarine earthquake with a magnitude of 7.5 could generate a 3.6 meter high, 24 minute tsunami at the source. Note that the 2004 tsunami off the Indonesia coast and the 2011 tsunami off the Japanese coast were caused by 9.3 and 9.0 magnitude earthquakes, respectively. The second important cause is the tsunamigenic submarine or terrestrial rapid landslide. Such landslides representing a rigid body motion along a slope-failure surface, are often triggered by earthquakes. In this case, a first order simplistic estimate relates tsunami height directly to the slide volume and sliding horizontal angle, and reciprocally to the water depth of incidence. One example of such a tsunami was the 1975 tsunami that occurred at the head of the Kitimat Arm of the Douglas Channel fjord system in British Columbia. A recent example is the Palu Indonesia Tsunami. A tsunami with a period in the order of 10s of minutes is classified as a long wave or a long-legged wave, and as pointed out in the Ocean Waves blog on the NATURE page, such waves occur when wave length is longer than 20 times the local water depth. Both the widths and lengths of crests and troughs of such long-period waves are measurable in scales of kilometers. Like all other waves, they are subjected to the transformation processes as soon as they are born, traveling very fast in deep water. The Transformation of Waves piece on this page has highlights of some of the wave transformation characteristics. Let me briefly describe some processes specific to long wave as they enter into the shallow water. . . . 2. Tsunami Propagation Hydrodynamics At least 3 processes of tsunami transformation are important – these are the processes of shoaling, funneling and resonance. The phenomena of shoaling and funneling can best be understood by applying the energy conservation principle, often known as the Green’s Law. This simple principle assuming no losses of energy by friction, etc., shows that for a gradually shoaling continental shelf, the ratio of height increase is proportional to the reciprocal of the ratio of depth decrease raised to the 1/4th power. For a channel gradually decreasing in width, the funneling effect is given by the ratio of height increase that is proportional to the reciprocal of the ratio of width decrease raised to the 1/2nd power. As a simple example of shoaling, a 3.6 meter high wave, will amplify to 6.4 meter as it transforms from 100 to 10 meter water depth. The phenomenon of resonance is quite interesting and intriguing because of its analogy to the force-response dynamics of an oscillating system. Resonance should not be confused with funneling – funneling occurs in the process of balancing the energy, while resonance is the frequency response of the system and occurs due to the reflection of and interaction with the incident wave. Let me try to explain it more based on my paper – Modeling Tsunami and Resonance Response of Alberni Inlet, British Columbia {30th International Conference on Coastal Engineering, World Scientific, 2006. This paper is one of the many papers listed by Prof. Robert L. Wiegel at the University of California, Berkeley as Tsunami Information Sources and published in 2009 in the Science of Tsunami Hazards – the International Journal of Tsunami Society. To get into the core concept of it, one needs to understand the behavior of an oscillating system. Such a system is characterized by a natural frequency at which it resonates to the exciting force – which means that the incident and reflected waves are virtually interlocked with each other, with very high anti-nodal amplification of the incident wave amplitude. In reality however, most natural systems do not respond to such an extent because of frictional damping etc. In addition, experiments with resonant behaviors show that a system also responds by amplification of the exciting wave both at sub- and super-resonant frequencies. This behavior is very important, and let me try to clarify how it explains the tsunami response of the Alberni Inlet. The 1964 Alaska tsunami registered about 1 meter high with a period of 90 minute at the entrance of Alberni Inlet at Bamfield, amplified to 3-times to cause huge damages at the head of the inlet at Port Alberni. The Alberni Inlet is a 65 km long deep fjord that virtually shows no phase lag or amplification in tidal motion. Such a system is very vulnerable because its natural frequency lies within the close range of usual tsunami frequencies. Contrary to the conclusions of previous investigators, my hydrodynamic modeling investigation with Mike21 (courtesy Danish Hydraulic Institute), showed that the 3-times amplification occurred at a sub-resonant frequency – and had there been an incident tsunami close to the resonant frequency, the amplification would have been some 5 times. Like all waves, a small tsunami in deep water shoals to monstrous waves as it propagates into the shallow water. After breaking Tsunami Run-ups flood coastal lands with enormous inbound and outbound speeds causing havoc and destruction. The arrival of Tsunami crest is preceded by the huge draw down or Sea Level Suck Out associated with the Tsunami trough. This phenomenon sucks out things from the shore out into the sea – exposing shoreline features – leaving many aquatic lives stranded in air. It catches offshore boats off-guard – and tragedies happen when people rush out to catch the stranded fishes. See more in the Frontal Wave Force Field in Force Fields in a Coastal System. . . . 3. Tsunami Run-up Well, so far so good. Now let us focus our attention on the most important aspect of tsunami effect – the runup (runup is the vertical height of tsunami propagation above mean water level) and loads on structures. Part of this discussion will be based on my short article published in the 2008 ASCE Journal of Waterway, Port, Coastal and Ocean Engineering {Discussion of ‘Maximum Fluid Forces in the Tsunami Runup Zone’}. Most tsunamis at their births belong to nonlinear wave category – and the degree of nonlinearity increases as they become taller and travel on to the shallow water. At a certain time, the tsunami wave becomes unsustainable as the water particle velocity exceeds the celerity (square root of the product of acceleration due to gravity and depth), and taking the shape of a solitary wave (a wave that does not have a trough) it breaks generating a very forceful bore that runs up the land. This process turns an oscillatory wave into a translatory one like that of a dam break flood wave. However, the difference between the flood wave and the tsunami translatory wave is that – the tsunami is not a single wave, but rather a series of waves that comes one after another with complicated hydraulic interactions of run ups and run downs. What is the maximum velocity of the tsunami bore? Investigations show that the maximum bore velocity is about 1.4 times the celerity (up to 2 times at the leading edge; celerity becomes defined in terms of tsunami height as there is no trough), or even higher when the propagating bores become constricted by topography and structures. As an example, a 1 meter high tsunami will likely to generate a 6.3 meter per second velocity at the leading edge, followed by a propagating velocity of 4.4 meter per second. In Froude (William Froude, 1810 – 1879) terms, the wave propagation speed exceeding the celerity is called the supercritical flow. Such flows could travel upstream, cross channels, roads and embankments unleashing the huge energy it posses. A water velocity of this kind has enormous power to destroy structural members and uproot them by scouring. . . . 4. Tsunami Forces on Structures Let us now turn our attention on the forces that tsunamis exert on structures standing on its way. When one thinks about it after witnessing the 2011 Japanese tsunami destructions, it is impossible for one not to wonder about the limitations of human capability in planning and designing measures to withstand the enormous wrath of a tsunami. This feeling arises because Japan is a reportedly tsunami savvy country – perhaps sophisticated in its engineering design standards and codes. Among the limited amount works in this field, a document prepared by US FEMA (Federal Emergency Management Agency) and US NOAA (National Oceanic & Atmospheric Administration) stands out in its comprehensiveness of discussing the problem. It cites the standards of flood resistant designs developed by ASCE/SEI (American Society of Civil Engineers/Structural Engineering Institute). According to the type and nature of forces, tsunami loads are identified as 8 types:
In addition to the enormous forces on structures, tsunamis also erode and scour shallow foundations undermining their stability. The opposite also happens in areas where sedimentation and debris dumps occur. Horizontal wave loads generally arise due to velocity (drag) and acceleration (inertia). Why only drag force is important for tsunamis? I would like to answer the question based on one of my papers {Wave Load on Piles – Spectral versus Monochromatic Approach, Proceedings, 18th International Offshore and Polar Engineering Conference, Vancouver, ISOPE, 2008}. It turns out that in low frequency (or high period) oscillations including flood waves, the inertial forces diminish in magnitude leaving the horizontal hydrodynamic loading processes on to the drag effect. I hope to talk more about it at some other time. We have talked about tsunami loads on structures located in the runup zone. How about structures – nearshore marine terminals and offshore oil platforms standing in water where a tsunami has not broken? In such cases, one needs to resort to nonlinear wave phenomena to determine the tsunami kinematics and loads. How about the effect of sea level rise (SLR) on tsunami? Well, there are no direct effects. However, with the raised mean water level, tsunamis will be able to travel more inland, and run up higher. The argument becomes clear, if one imagines the 2004 and 2011 tsunamis to occur a century later when the SLR stand is likely to be higher. . . . Here is an anecdote to ponder: The disciple said, “Sir, I am feeling very happy today. Someone greeted me with a smile as I was walking by.” The master looked at his disciple and said, “Well, I am very glad to hear that. You seem to be in the right mood to receive the greeting. Reciprocally, your reaction must have made the greeting person happy.” . . . . . - by Dr. Dilip K. Barua, 6 October 2016  This piece is a continuation of the Sea Level Rise – the Science post on the Nature page. Let us attempt to see in this piece how different thoughts are taking shape to face the reality of the consequences of sea level rise (SLR). The consequences are expected across the board – in both biotic and abiotic systems. But to limit this blog to a manageable level, I will try to focus – in an engineering sense – on some aspects of human livelihood in frontal coastal areas – some of the problems and the potential ways to adapt to the consequences of SLR (In a later article Warming Climate and Entropy, posted in December 2019 – I have tried to throw some lights on the climate change processes of the interactive Fluid, Solid and Life Systems on Earth – the past, the present and the future).
Before doing that let us revisit one more time to point out that all familiar lives and plants have a narrow threshold of environmental and climatic factors, within which they can function and survive. This is in contrast to many microorganisms like Tardigrades, which can function and survive within a wide variation of factors. Therefore adaptation can be very painful, even fatal when stresses exceed the thresholds quickly – in time-scales shorter than the natural adaptation time. . . . 1. SLR Imposition 1.1 Stress What is stress? Global warming and SLR literature use this term quite often. Stress is part of the universal cause-effect, force-response, action-reaction, stress-consequence duo. In simple terms and in context of this piece, global warming is the stress with SLR as the consequence – in turn SLR is the stress with the consequences on human livelihood in the coastal zone. Again, as I have mentioned in the previous piece, the topic is very popular and literature are plentiful with discussions and opinions. The main resources consulted for this piece are the adaptation and mitigation chapters of the reports worked on by: UN entity IPCC (Intergovernmental Panel on Climate Change), US NOAA (National Oceanic and Atmospheric Administration), and USACE (United States Army Corps of Engineers). 1.2 Vulnerability Before going further, it will be helpful to clarify the general meanings of some of the commonly used terms – these terms are used in contexts of system responses and reactions – susceptibility, prevention, the ability to adjust to changes, and the ability to cope with repeated disruptions. The first is vulnerability – the susceptibility and inability of a system to cope with adverse consequences or impacts. One can simply cite an example that human habitation, coastal and port infrastructure in low lying areas are more vulnerable to SLR than those lying in elevated areas – and so are the developing societies than the developed ones. 1.3 Mitigation The second is known as mitigation – the process of reducing the stresses to limit their impacts or consequences. We have seen in the NATURE page that there could be some 8 factors responsible for SLR. But scientists have identified that the present accelerated SLR is due to the continuing global warming caused by increased concentration of greenhouse gases. This anthropogenic factor is in human hands to control; therefore reducing greenhouse gases is one of the mitigation measures. 1.4 Adaptation The third is adaptation – the process of adjusting to the consequences of expected or imposed stresses, in order to either lessen or avoid harm, or to exploit beneficial opportunities. This is the primary topic of this piece – how humans could adjust to the consequences of SLR. The fourth is closely related to adaptation and is known as resilience – the ability to cope with repeated disruptions. It is not difficult to understand that adaptation process can become meaningless without resilience. Also to note that a successful mitigation can only work with some sort of adaptation – for example, adaptation by innovating new technologies to control and limit greenhouse gas emission. However, one may often require to compromise or make trade-offs between mitigation and adaptation processes to chalk out an acceptable solution. . . . 2. SLR Consequences I have included an image (credit: anon) of human habitation and township developed on a low lying barrier island. Similar developments occur in most coastal countries – some are due to the pressure of population increase, while others are due to the lack of foresight and understanding by regulating authorities. Such an image is important to look at, to reflect on and to think about human vulnerability, and the processes of mitigation, adaptation and resilience to the consequences of SLR. A series of ASCE Collaborate discussions gives a glimpse of SLR on low-lying airports. . . . 2.1 Enhanced Wave Activity Before going further, some aspects of climate change that exacerbate the SLR effects need to be highlighted. The first is the enhanced wave activity associated with SLR. We all have seen the changing nature of waves sitting on a shoreline during an unchanging weather condition – less wave activity at low tide and enhanced waves as tide rises. Why does that happen? One reason is the depth-limited filtering of wave actions – for a certain depth only waves smaller than about 4/5th of water depth could pass on to the shore without breaking. Therefore, as the water level rises with SLR, the numbers of waves propagating on to the shore increase. The second is the enhanced storminess caused by global warming. All the climate change studies indicate the likelihood of increase in storminess both in intensity and frequency – and perhaps we are witnessing symptoms of that already. High wind storms are accompanied by high storm surges and waves together with torrential rainfall and terrestrial flooding. . . . 2.2 Inundation and Others What are other consequences of SLR? The consequences are many – some may not even be obvious at the present stage of understanding. They range from transgression of sea into the land by erosion, inundation and backwater effect, to salt-water intrusion, to increased forces on and overtopping of coastal waterfront structures. If the 2.0 meter SLR really (?) happens by the end of the 21st century, then it is impossible for one not to get scared. I have included a question mark to the 2.0 meter SLR because of the high level of uncertainty in the predictions by different organizations (see the Sea Level Rise – the Science blog on the NATURE page). For such a scenario, the effective SLR is likely to be no less than 10.0 meter affecting some 0.5 billion coastal population. The effective SLR is an indication of the range of consequences that a mean SLR would usher in. Let me try to provide a brief outline of the consequences. First, one should understand that the transgression of sea into the land is not like the invasion by a carpet of water gradually encroaching and inundating the land. It is rather the incremental incidences of high-tide-flooding combined with high wave activity. The result is the gradual net loss of land into the sea through erosion and scour, sediment-morphological readjustments and subsequent submergence. What adaptation to SLR really means? Let us think of coastal population first. Survival instinct will lead people to abandon what they have, salvage what they can, and retreat and relocate themselves somewhere not affected by SLR. Although some may venture to live with water around if technological innovations come up with proven and viable measures. There are many traditional human habitations in seasonally flooded low lands, and also examples of boathouses around the world. Therefore, people’s lives are not so much at stake in direct terms; it is rather the monetary and emotional losses they would incur – losses of land, home and all of their valuable assets and memories. This adaptation process will not be equally felt by all the affected people. Rich people and perhaps many in developed societies are likely to cope with the problem better than the others. . . . 2.3 Civil Infrastructure Perhaps the crux of the problem will be with civil infrastructure. One can identify them as four major types:
Some other aspects of the problem lie with the intrusion of sea saline water into estuaries, inlets and aquifers. Coastal manufacturing and energy facilities requiring freshwater cooling will require adapting to the SLR consequences. The problem will also be faced with the increased corrosion of structural members. What to do with this huge problem of the existing civil infrastructure? What does adaptation mean for such a problem? One may think of renovation and reinforcement, but the likelihood of success of such an adaptive approach may be highly remote. How do the problems translate to the local and state’s economy? What about abandoning them to form submersed reef – declaring them as Water Park or sanctuary? - leaving many as remnants for posterity like the lost city of Plato’s (Greek Philosopher, 423 – 347 BCE) Atlantis? There are no easy answers to any of these questions; but there is no doubt that stakes are very high. We can only hope that such scenarios would not happen. What is important and is being initiated across the board is the formulation of mitigation and adaptation strategies and policies. Such decision making processes rely on the paradigm of risk minimization – but can only be meaningful if uncertainties associated with SLR predictions are also minimized. One important area of work where urgent attention is being paid is in the process of updating and redefining the standards, criteria and regulations required for robust planning and design of new coastal civil infrastructure. However, because of uncertainties in SLR predictions even this process becomes cumbersome. Placing concrete and steel to build anywhere is easy, what is not easy is envisioning the implications and the future. Here is a ASCE Forum Discussion Piece on climate conditions non-stationarity, and implications for relevant civil engineering standards. Apart from the 2017 NAP Proceedings – 24847 Responding to the Threat of Sea Level Rise, the 2010 publication – 12783 Adapting to the Impacts of Climate Change is an excellent read on possible options – as approaches to adapt to different stresses and consequences imposed by climate change. Well, some thoughts in a nutshell, shall we say? But mitigation of and adaptation to a complex phenomenon like global warming, climate change and SLR must be understood as an evolving process – perfection will only likely to occur as things move forward. And one should not forget that the SLR problems as complex and intimidating as they are, are slow in human terms – therefore the adaptation processes should be conceived in generational terms, but all indications suggest that the thinking and processes must start without delay. Fortunately all members of the public are aware of the problem and are rightly concerned - whether or not things are rolling in the right direction. Hopefully, this will propel leaders to take thoughtful actions. . . . 3. An Overview of the 2021 IPCC Assessment What does the 2021 IPCC – AR6 say about the risks associated with SLR? In its WGII Technical Summary – probable risks posed by enhanced sea level rise – have been spelled out in different confidence scales. The assessments and predictions are based on field observations/evidences and climate modeling efforts of different sorts (see modeling basics in Water Modeling). And three other WIDECANVAS articles: Warming Climate and Entropy, Uncertainty and Risk and The World of Numbers and Chances can help understanding the IPCC scale. This qualitative scale is defined in a matrix of evidence vs agreement – with the agreement indicating the degree of conformity between observations and the results of analytical tools or models. When an assessment is rated up to a sufficiently defensible scale – it is subjected to quantification in a way to define the probability of occurrence and labeling it in likelihood terms. Here is a gist of IPCC findings and suggestions: Coastal risks will increase by at least one order of magnitude over the 21st century due to committed sea level rise impacting ecosystems, people, livelihoods, infrastructure, food security, cultural and natural heritage and climate mitigation at the coast. Concentrated in cities and settlements by the sea, these risks are already being faced and will accelerate beyond 2050 and continue to escalate beyond 2100, even if warming stops. Historically rare extreme sea level events will occur annually by 2100, compounding these risks (high confidence) . . . Under all emissions scenarios, coastal wetlands will likely face high risk from sea level rise in the mid-term (medium confidence), with substantial losses before 2100. These risks will be compounded where coastal development prevents upshore migration of habitats or where terrestrial sediment inputs are limited and tidal ranges are small (high confidence). Loss of these habitats disrupts associated ecosystem services, including wave-energy attenuation, habitat provision for biodiversity, climate mitigation and food and fuel resources (high confidence). Near- to mid-term sea level rise will also exacerbate coastal erosion and submersion and the salinisation of coastal groundwater, expanding the loss of many different coastal habitats, ecosystems and ecosystem services (medium confidence) . . . The exposure of many coastal populations and associated development to sea level rise is high, increasing risks, and is concentrated in and around coastal cities and settlements (virtually certain). High population growth and urbanisation in low-lying coastal zones will be the major driver of increasing exposure to sea level rise in the coming decades (high confidence). By 2030, 108–116 million people will be exposed to sea level rise in Africa (compared to 54 million in 2000), increasing to 190–245 million by 2060 (medium confidence). By 2050, more than a billion people located in low-lying cities and settlements will be at risk from coast-specific climate hazards, influenced by coastal geomorphology, geographical location and adaptation action (high confidence) . . . Under all climate and socioeconomic scenarios, low-lying cities and settlements, small islands, Arctic communities, remote Indigenous communities and deltaic communities will face severe disruption by 2100, and as early as 2050 in many cases (very high confidence). Large numbers of people are at risk in Asia, Africa and Europe, while a large relative increase in risk occurs in small island states and in parts of North and South America and Australasia. Risks to water security will occur as early as 2030 or earlier for the small island states and Torres Strait Islands in Australia and remote Maori communities in New Zealand. By 2100, compound and cascading risks will result in the submergence of some low-lying island states and damage to coastal heritage, livelihoods and infrastructure (very high confidence). Sea level rise, combined with altered rainfall patterns, will increase coastal inundation and water-use allocation issues between water-dependent sectors, such as agriculture, direct human consumption, sanitation and hydropower (medium confidence) . . . Risks to coastal cities and settlements are projected to increase by at least one order of magnitude by 2100 without significant adaptation and mitigation action (high confidence). The population at risk in coastal cities and settlements from a 100-year coastal flood increases by approx. 20% if the global mean sea level rises by 0.15 m relative to current levels, doubles at 0.75 m and triples at 1.4 m, assuming present-day population and protection height (high confidence). For example, in Europe, coastal flood damage is projected to increase at least 10-fold by the end of the 21st century, and even more or earlier with current adaptation and mitigation (high confidence). By 2100, 158–510 million people and USD7,919–12,739 billion in assets are projected to be exposed to the 1-in-100-year coastal floodplain under RCP4.5, and 176–880 million people and USD8,813–14,178 billion assets under RCP8.5 (high confidence). Projected impacts reach far beyond coastal cities and settlements, with damage to ports potentially severely compromising global supply chains and maritime trade, with local to global geopolitical and economic ramifications (medium confidence). Compounded and cascading climate risks, such as tropical cyclone storm surge damage to coastal infrastructure and supply chain networks, are expected to increase (medium confidence) . . . Particularly exposed and vulnerable coastal communities, especially those relying on coastal ecosystems for protection or livelihoods, may face adaptation limits well before the end of this century, even at low warming levels (high confidence). Changes in wave climate superimposed on sea level rise will significantly increase coastal flooding (high confidence) and erosion of low-lying coastal and reef islands (limited evidence, medium agreement). The frequency, extent and duration of coastal flooding will significantly increase from 2050 (high confidence), unless coastal and marine ecosystems are able to naturally adapt to sea level rise through vertical growth and landward migration (low confidence). Permafrost thaw, sea level rise, and reduced sea ice protection is projected to damage or cause loss to many cultural heritage sites, settlements and livelihoods across the Arctic (very high confidence). Deltaic cities and settlements characterised by high inequality and informal settlements are especially vulnerable (high confidence). Although risks are distributed across cities and settlements at all levels of economic development, wealthier and more urbanised coastal cities and settlements are more likely to be able to limit impacts and risk in the near- to mid-term through infrastructure resilience and coastal protection interventions, with highly uncertain prospects in many of these locations beyond 2100 (high confidence). Prospects for enabling and contributing to climate resilient development thus vary markedly within and between coastal cities and settlements (high confidence). RCP stands for Representative Concentration Pathway. One can pass detailed review comments on many of the IPCC findings and suggestions. Let us not go in that direction – instead, I will point to some crucial aspects that escaped IPCC reporting and investigations. In brief, these omissions include: SLR induced enhancement of and changes in the water motion dynamics along coastal waterfront and shores. These are likely to be manifested in such areas as – wave, tide, circulation, extreme events like storm surge and tsunami, and shoreline changes associated with sediment-morphology dynamics due to such forcing. What are the characterizations of such crucial changes? What are the impacts of SLR on the probable redistribution and enhancement of Force Fields in a Coastal System, and associated implications? . . . Here is an anecdote to ponder: The disciple said, “Sir, adaptation is a very strong word perhaps more than what we think it is.” The master replied, “Yes, it does have a deeper meaning. One is in the transformation of the personalities undergoing the adaptation processes. It is a slow and sequential process ensuring the fluidity of Nature and society and evolution. If one thinks about the modern age of information, travel and immigration, the process is becoming much more encompassing – perhaps more than we are aware of. But while slow adaptation is part of the natural process, the necessity of quick adaptation can be very painful and costly.” . . . . . - by Dr. Dilip K. Barua, 29 September 2016  With this piece I am breaking my usual 3-3-3 cycle of posting on the NATURE, SOCIAL INTERACTIONS and SCIENCE & TECHNOLOGY pages. The reason is partly due to the comment of one of my friends who said, it is nice reading the Nature and Science & Technology pages. Hope you would share more of your other experiences in theses pages. Well, I have wanted to that but in the disciplined order of 3-3-3 postings. But this does not mean that the practice cannot be changed to concentrate more on the technical pages. Let us see how things go – a professional experience spanning well over 3 decades is long enough to accumulate many diverse and versatile humps and bumps, distinctions and recognitions, and smiles and sadness.
This piece can be very long, but I will try to limit it to the usual 4 to 5 pages starting from where I left – some of the model basics described in the Natural Equilibrium essay on the NATURE page, and in the Common Sense Hydraulics essay on this page. To suit the interests of general members of the public, I will mainly focus on the practical aspects of water modeling rather than on numerical aspects. A Collaborate-ASCE discussion link highlights aspects of water modeling validation issues. . . . 1. Reality to Modeling The title of this piece could have been different – numerical modeling, computational modeling, hydrodynamic modeling, wave modeling, sediment transport modeling, morphological modeling . . . Each of these terms conveys only a portion of the message what a modeling of Natural water means. The Natural waters in a coastal environment are 3-dimensional – in length, width and depth, subjected to the major forces – externally by tide and wave at the open boundaries, wind forcing at the water surface and frictional resistance at the bottom. The bottom can be highly mobile like in alluvial beds, or can be relatively fixed like in a fjord. Apart from these regular forcings coastal waters are also subjected to extreme episodes of storm surge and tsunami. A model generally refers to a collective term for: ‘representations of essential system aspects, with knowledge being presented in a workable form.’ (Delft Hydraulics 1999). A system refers to: ‘A system is a part of reality (isolated from the rest) consisting of entities with their mutual relations (processes) and a limited number of relations with the reality outside of the system.’ A model, therefore, is the representation of a system if it describes the structure of the system-entities and relations. Models can be depicted in all different kinds of presentations: ordinary languages, schematics, figures, mathematics, etc. A mathematical model describing the relations in terms of independent and dependent variables is the mathematical translation of a conceptual model. Non-mathematical representation of system aspects is known as the conceptual model. A schematic of different hydraulic models and relevant understandings is presented in the image. This image is taken from my draft lecture note – prepared for the students, while teaching at the Florida Institute of Technology. . . . 1.1 Selecting an Appropriate Model While the Natural coastal setting is 3-dimensional, it is not always necessary to treat the system as such in a model. Depending on the purpose and availability of appropriate data, coastal systems can be approximated as 2-dimensional or 1-dimensional. The 2-dimensional shallow-water approximation is possible especially when the aspect ratio (depth/width) is low. When a channel is very long and the aspect ratio is relatively high, it can even be modeled as 1-dimensional. Apart from these dimensional approximations, some other approximations are also possible because all terms of the governing equations do not carry equal weight. I have tried to highlight how to examine the importance of different terms in a conference presentation (A Dynamic Approach to Characterize a Coastal System for Computational Modeling and Engineering. Canadian Coastal Zone Conference, UBC, 2008). The technique known as scale analysis lets one to examine a complicated partial differential equation by turning it into a discrete scale-value-equation. My presentation showing the beauty of scale analysis is highlighted for the governing hydrodynamics of fluid motion – the Navier-Stokes Equation (Claude-Louis Navier, 1785 – 1836 and George Gabriel Stokes, 1819 – 1903). It was further demonstrated in my Encyclopedia article, Seabed Roughness of Coastal Waters for practical workable solutions. The technique can also be applied for any other equation – such as the integral or phase-averaged wave action equation, and the phase resolving wave agitation equation. Many investigators deserve credit for developing the phase-averaged wave model – which is based on balancing the wave energy-action. The phase-resolving wave model is based on the formulation by Boussinesq – the French mathematician and physicist Joseph Valentin Boussinesq (1842 – 1929). The latter is very useful in shallow-water wave motions associated with non-linearity and breaking, and in harbors responding to wave excitation at its entrance. . . . 1.2 Modeling Creativity and Constraints A Power Point presentation of model-simulated south-bound longshore currents that could develop during an obliquely incident storm wave from the northeast is shown in Littoral Shoreline Change in the Presence of Hardbottom – Approaches, Constraints and Integrated Modeling. This title was presented at the 22nd Annual National Conference on Beach Preservation Technology, St. Pete Beach, Florida, 2009 on behalf of Coastal Tech. The incident wave is about 4 meter high generated by a Hurricane Frances (September 5th 2004) like storm on the Indian River County shores in Florida. Water modeling is fundamentally different and perhaps more complex – for example, from structural stability and strength modeling and computations. This assertion is true in a sense that a water model first aims to simulate the dynamics of Natural flows to a reasonable level of acceptance, before more can be done with the model – to use it as a soft tool to forecast future scenarios, or to predict changes and effects when engineering interventions are planned. Water modeling is like a piece of science and art, where one can have a synoptic view of water level, current, wave and sediment transport, and bed morphology within the space of the model domain simultaneously – this convenience cannot be afforded by any other means. If the model results are animated, one can see how the system parameters evolve in response to forces and actions – this type of visuals is rather easy and instructive for anyone to understand the beauty and dynamics of fluid motion. For modelers, the displays elevate his or her intuition helping to identify modeling problems and solutions. . . . 1.3 Analytical vs Numerical Modeling Before going further, I would like to clarify the two terms I have introduced in the Coastal River Delta blog on the NATURE page. These two terms are behavioral model and process-based model. Let me try to explain the meaning of these two terms briefly by illustrating two simple examples. The simple example of a behavioral model is the Bruun Rule or the so-called equilibrium 2/3rd beach profile, proposed by Per Bruun in 1954 and refined further by Bob Dean (Robert G. Dean, 1931 – 2015) in 1977. The relation simply describes a planer (no presence of beach bars) beach depth as the 2/3rd power of cross-shore distance – without using any beach-process parameters such as the wave height and wave period. The only other parameter the Rule uses is the sand particle settling velocity. This type of easy-to-understand behavioral models that does not look into the processes exciting the system, exists in many science and engineering applications. The behavioral models capture response behaviors that are often adequate to describe a particular situation – however they cannot be applied or need to be updated if the situation changes. The simple example of a process-based model is the Chezy Equation (Antoine Chezy, 1718 – 1798) of the uniform non-accelerating flow – that turns out to have resulted from balancing the pressure-gradient force against the frictional resistance force. In this relation velocity of flow is related to water depth, water level slope (or energy slope) and a frictional coefficient. The advantage of a process-based model is that it can be applied in different situations, albeit as an approximation in which it has been derived. Let us now turn our attention to the core material of this piece – the numerical water modeling. The aspects of the scale modeling used to reproduce water motion in a miniature replica of the actual prototype in controlled laboratory conditions are not covered in this piece. These types of models are based on scale laws by ensuring that the governing dimensionless numbers are preserved in the model as in the prototype. I have touched upon a little bit of this aspect in the Common Sense Hydraulics piece on this page. I have been introduced to programming and to the fundamentals of numerical water modeling in the academic programs at IHE-UNESCO and at the USC. My professional experience started at the Land Reclamation Project (LRP) with the supports from my Dutch colleagues and participating in the hydrodynamic modeling efforts of LRP. Starting with programmable calculators, I was able to develop several hydraulic processing programs and tools – later translating them to personal computer versions. I must say, however that my knowledge and experience have really taken-off and matured during my heavy involvement with numerical modeling efforts in several projects in Canada, USA and overseas. This started with a model selection study I conducted with UBC for the Fraser River in British Columbia. A little brief on my modeling experiences. They include the systems: 8 in British Columbia (e.g. 2006 Coastal Engineering Tsunami paper), 1 in Quebec, 1 in Newfoundland and Labrador, 2 in Florida, 1 in Texas and 1 in Virginia (ASCE Ports 2013 Inlet Sedimentation paper). Among the modeled processes were hydrodynamics, wave energy actions, wave agitations, coupled wave-hydrodynamics, and coupled-wave-hydrodynamics-sediment transport-morphologies. The model forcings were tide, wind and wave, storm surge and tsunami. I will try to get back to some of the published works at some other time. Perhaps it is worthwhile to mention here that modeling experience is also a learning exercise; therefore one can say that all hydraulic engineers should have some modeling hand-on experiences, because they let him or her to acquire very valuable insights on hydraulics – simply using available relations to compute forces and parameters may prove incomplete and inadequate. . . . 2. Sources of Model Uncertainties In the Uncertainty and Risk piece on this page, some unavoidable limitations and constraints of models are discussed. Let me try to outline them in some more details. Model uncertainties can result from 8 different sources:
. . . 3. Model Validation Before a model is ready for application, it requires going through a process of validation. This process of comparing model outputs against corresponding measurements leads to tuning and tweaking of parameters to arrive at acceptable agreements. It is also reinforced with sensitivity analysis to better understand the model responses to parameter changes. A National Academies Publication discusses some important steps on model verification and validation. In Natural Equilibrium piece – here are what outlined: For modelers, the challenges are to translate the continuum of space and time into the discretized domain of a model – such as: what to include, what to leave out, what to smooth out, and what are the consequences for such actions. How best to take account of practical constraints and describe forcing at the boundaries to be realistic but at the same time avoiding model instability. Reactive forces like frictional resistance are notoriously non-linear – therefore it is important to watch how parameterization of these forces affects results. Let us attempt to understand this crucial steps by proposing an acronym: MRCAP – Model-Reality Conformity Assurance Processes . . . 3.1 Model-Reality Conformity Assurance Processes (MRCAP) The conformity of a model with the reality of interest is an important issue – not only for computational modeling – but also for any sort of modeling – including scale modeling. Large civil engineering practices and projects – especially its open-water hydraulic engineering tenet – are highly dependent on both of these modeling efforts. Scale modeling is continuously getting marginalized because of its cost – also, because of the growing robustness of and confidence in numerical models. Models are a replicating tool of a certain physical reality. Like with developing any tool – and before being assured as a validated product – they need experimentation, refinement and calibration to satisfy the governing laws and equations. Yet, models are a soft tool that accompany uncertainties of different sorts. But, the same is true with any physical reality – the quantitative nature of which can only be understood through measurements or sampling (more in Uncertainty and Risk). I like to begin explaining this interest aspect of water modeling with the help of MRCAP – Model-Reality Conformity Assurance Processes. The purpose of MRCAP is to produce a credible or conformal simulation of the reality. This reality can either be the system of as is existing conditions, or in combination with the envisioned scenarios of engineering installations. The latter is to examine and determine the forces on and effects of such interventions. An engineer’s computational modeling interest lies in both of them – and in the context of this article – in computational modeling of waters. At least four reference materials must be cited while explaining MRCAP. The first is the 1998 document (The Guide for the Verification and Validation of Computational Fluid Dynamics Simulations, AIAA Guide 1998). Many subsequent publications on this interesting topic trace their roots to this guide. They include: Oberkampf et al (Verification and Validation for Modeling and Simulation in Computational Science and Engineering Applications 2002); ASME 2020 (Standard for Verification and Validation in Computational Solid Mechanics); and the 2024 NAP Publication # 27747 (Quality Processes for Bridge Analysis Models). They provide the essence of a broad MRCAP framework. These reference materials shows MRCAP as consisting of three processes – starting with qualification, to verification and validation. The emphasis on these three processes form a loop of three end points: Reality ↔ Mathematical Model ↔ Computational Model ↔ Reality. The iterative processes between the first two was termed as ‘Model Qualification’. In 1979, the Society for Computer Simulation defined it as: “Determination of adequacy of the conceptual model to provide an acceptable level of agreement for the domain of intended application.” The term ‘conceptual model’ has been replaced by mathematical model in later evolution of definitions. Here is something from Natural Equilibrium: The workable form of a model can be concepts, ordinary language, schematics, figures and mathematics. A conceptual model is a non-mathematical representation of the inter-relationship of system elements. A mathematical model is the translation of a conceptual model in mathematical terms of variables and numbers. This step essentially indicates processes of examining and re-examining the Representitiveness of the selected mathematical model with reality. The degree of representitiveness is the first of the 8 model uncertainties. Next, the iterative processes between the selected mathematical model and the implemented computational model was termed as ‘Verification’. In ASME wording, verification is: “the process of determining that a computational model accurately represents the underlying mathematical model and its solution”. Among the 8 sources of uncertainties, the degree of Empiricism, Discretization of the Continuum, Iteration to Convergence, Rounding-Off and Numerical Code tells to what extent the verification processes are successful. The first four sources of uncertainties are listed as 2 – 5, the last one is listed 8. ‘Validation’ processes comprise the final step connecting the Computational Model with Reality. The degree of the rest two sources of uncertainty, 6 and 7, Application and Modeler determine how validation processes are successful. Again, in ASME wording validation is: “the process of determining the degree to which the model is an accurate representation of corresponding physical experiments from the perspective of the intended uses of the model” In the broad framework of modeling terminology – the AIAA guide emphasizing verification and validation is known as V&V. . . . 4. Evaluating Model Performance The V&V framework misses something very important – at least from computational water modeling perspective of model performance. This something is known as ‘Calibration’ – a crucial step. Calibration is an iterative process where a modeler tweaks terms and parameters to tune and fine-tune a computational model. Also, the modeler uses the term verification in a different sense than what is described the AIAA guide. To avoid confusion, let us term it as ‘Model Results Verification’ This step is an essential confidence building exercise of MRCAP – and is done by simulating a scenario – that is different in time and space than the calibration scenarios. It is important to understand these aspects further. Let me begin with a short introduction – focusing primarily on Coastal Water Modeling. Wave, hydrodynamic and sediment transport computational modeling activities occupy a significant portion of analysis in coastal engineering, and form an integral component of complex and large projects. Although interchangeably used, a distinction has to be made between the terms known as numerical and computational modeling. While numerical modeling mainly deals with transforming complex differential equations describing the physics – into algebraic equations and to numerical codes; computational modeling is the art of transforming a physical problem to the computational domain of a numerical model and executing simulations to replicate the physics. The fundamental to all these efforts is the use of a computer which cannot handle complex differential equations, but can work with numbers generated by algebraic equations and codes to perform these operations. A person can either be a numerical modeler, a computational modeler or both. In the past, there was no such distinction, but this is becoming more evident as modeling efforts continue to proliferate and expand – with the availability of many commercial modeling software suites. The rationale for calibration, and model results verification can be appreciated from the requirements expected of modelers. They must understand: (1) the theory of physics being modeled; (2) the basics of numerical modeling formulation; (3) the computational methods of the model being applied; (4) the processes describing the area of application including initial and boundary conditions; (5) dynamic coupling of wave, hydrodynamics, and sediment transport-morphology, if applicable; (6) the wave and hydrodynamic interactions with structures, if present; (7) uncertainties present both in measurements and model outputs; (8) tuning of model parameters by calibration and verification; (9) interpretation of model outputs to the tune of conformity assurance; (10) last, but not the least, the pre- and post-processing of computational inputs and outputs. More in a ASCE Discussion Post. In my 2009 FSBPA Power Point Presentation (Barua, Walther, Triutt; 2009. Littoral Shoreline Change in the Presence of Hard Bottom – Approaches, Constraints and Integrated Modeling), I have tried to shed light on two aspects of model uncertainties and constraints – resulting primarily from model data sources. In most cases of coastal water computational modeling – modelers have to deal with and use data available from regional sources – the quality of them – are really not known. In addition, quantity, resolution and frequency of such available data are mostly inadequate. These constraints impose limitations on the modeler’s efforts to calibrate and verify the model. This can be compared with the site-specific dedicated measurements campaign for large projects – where a modeler has control on measurement quantity, quality, resolution and frequency. . . . 4.1 Statistical Assessments of Model Performance Finally, a few words on the rationale of such requirements, and on the statistical assessments of model performance – leading to the soundness of MRCAP. The rationale for calibration and verification can best be understood by recognizing the various elements and terms of the governing equations – that are complete with the actions of some reactive forces (referred to as closure terms in early literature). In hydrodynamic equations the reactive forces appear as solid boundary roughness and fluid-flow turbulence – nature of turbulence. These forces are parameterized in the governing equations – therefore, can be tweaked to attain an equilibrium of forces ↔ responses. The processes also include various levels of sensitivity analyses. A few statistical assessments are made comparing model results with relevant measurements. They include: Mean Absolute Error (MAE), Root Mean Square Error (RMSE), Brier Skill Score (BSS; or Assessment BSA). When MAE is divided by the average of the measured parameter, it turns into RMAE. A modeler goes through the iterative processes of calibration and verification to minimize MAE, RMSE or RMAE errors, while trying to maximize BSS. Use of statistics is an attempt to smooth out disagreements assuming that for a certain value of the statistical parameter – the model performance is acceptable. According to the suggestions by Van Rijn et al (2003) the good criteria are indicated by the following: 0.05 < RMAE of wave height < 0.1; 0.1 < RMAE of velocity < 0.3; 0.6 < BSS of bed level change <0.8. In the processes of rating a finding – IPCC (see 2021 IPCC – AR6) employs a two-step process to describe uncertainty. First, a qualitative confidence scale is defined in a matrix of evidence vs agreement – with the agreement indicating the degree of conformity between reality or evidence – and the results of analytical tools or models. In this step, both observations of reality and model results are screened and scrutinized. Next, when the confidence graduates to a sufficiently defensible scale – it is subjected to quantification in a way to define the probability of conformity – finishing it with likelihood labeling. In their own words, as in the WGI Report: . . . Two calibrated approaches are used to communicate the degree of certainty in key findings . . . (1) Confidence is a qualitative measure of the validity of a finding, based on the type, amount, quality and consistency of evidence (e.g., data, mechanistic understanding, theory, models, expert judgment) and the degree of agreement . . . (2) Likelihood provides a quantified measure of confidence in a finding expressed probabilistically (e.g., based on statistical analysis of observations or model results, or both, and expert judgement by the author team or from a formal quantitative survey of expert views, or both). Where there is sufficient scientific confidence, findings can also be formulated as statements of fact without uncertainty qualifiers . . . . . . I have often been asked whether water modeling is worth the efforts and costs. My unequivocal answer to the question is yes. In this age of quickly improving digital computations, displays, animations and automations, it would be a shame if one thinks otherwise. Science and engineering are not standing still – the capability of numerical models is continually being refined and improved at par with the developments of new techniques in the computing powers of digital machines. Like all project phases, a water model can be developed in phases – for example, starting with a course and rough model with the known regional data. Such a preliminary model developed by experienced modelers can be useful to develop project concepts and pre-feasibilities, and can also help planning measurements for a refined model required at subsequent project phases. We have tried to conclude that a model is a soft tool; therefore its performance in simulation and prediction is not expected to be exact. This means that one should be cautious not to oversell or over-interpret what a model cannot do. But even if a water model is not accurate enough to be applied as a quantitative tool, it can still be useful for qualitative and conceptual understandings of fluid motion, in particular as a tool to examine the effectiveness and effects of engineering measures under different scenarios. . . . Here is an anecdote to ponder: The disciple asked the master, “Sir, what does digitization mean to social fluidity or continuity?” The master replied, “Umm! Imagine a digital image built by many tiny pixels to create the totality of it. Each of these pixels is different, yet represents an essential building block of the image puzzle. Now think of the social energy – the energy of the harmonic composite can similarly be high and productive when each building block has the supporting integrity and strength.” . . . . . - by Dr. Dilip K. Barua, 22 September 2016 |
Dr. Dilip K Barua
Archives
October 2024
Categories |
RSS Feed
